さて、正規型ユニバーサルジョイントを２つ組み合わせたときの\(\theta\)と\(\xi\)との関係は、

\(tan(\xi)=\frac{sin(\delta)+tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta)-tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

で、簡易型ユニバーサルジョイントを２つ組みわ合わせたときの\(\theta\)と\(\xi\)との関係は、

\(tan(\xi) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta)\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\cdot cos(\beta)\)

で表現されるのでした。

２つの式は似ているようで異なりますが、これはどういうことを意味しているのでしょうか。

簡易型ユニバーサルジョイントを２つ組み合わせたときの式に、\(\theta = \theta^\prime  – \frac{\pi}{2}\)、\(\xi = \xi^\prime + \frac{\pi}{2}\)、を代入して変形します。

\(tan(\xi^\prime + \frac{\pi}{2}) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta^\prime – \frac{\pi}{2})\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta^\prime  – \frac{\pi}{2})\cdot sin(\delta)}\cdot cos(\beta)\)

\(tan(\theta +\frac{\pi}{2}) = tan(\theta -\frac{\pi}{2}) = -\frac{1}{tan(\theta)}\)ですので、上記の式は

\(-\frac{1}{tan(\xi^\prime)} = \frac{sin(\delta)\cdot cos(\alpha) -\frac{1}{tan(\theta^\prime)}\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)+\frac{1}{tan(\theta^\prime)}\cdot sin(\delta)}\cdot cos(\beta)\)

となり、これを\(tan(\xi^\prime)\)について変形します。

\(tan(\xi^\prime) = -\frac{cos(\delta)\cdot cos(\alpha)+\frac{1}{tan(\theta^\prime)}\cdot sin(\delta)}{sin(\delta)\cdot cos(\alpha) -\frac{1}{tan(\theta^\prime)}\cdot cos(\delta)}\cdot \frac{1}{cos(\beta)}\)

右辺の分数の分子と分母とに\(tan(\theta^\prime)\)をかけ、式を整理すると、

\(tan(\xi^\prime) = \frac{sin(\delta) + tan(\theta^\prime)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta) – tan(\theta^\prime)\cdot sin(\delta)\cdot cos(\alpha) }\cdot \frac{1}{cos(\beta)}\)

を得ます。この式を見ると、正規型ユニバーサルジョイントを２つ組み合わせた場合の\(\theta\)と\(\xi\)との関係の式と同じであることがわかります。

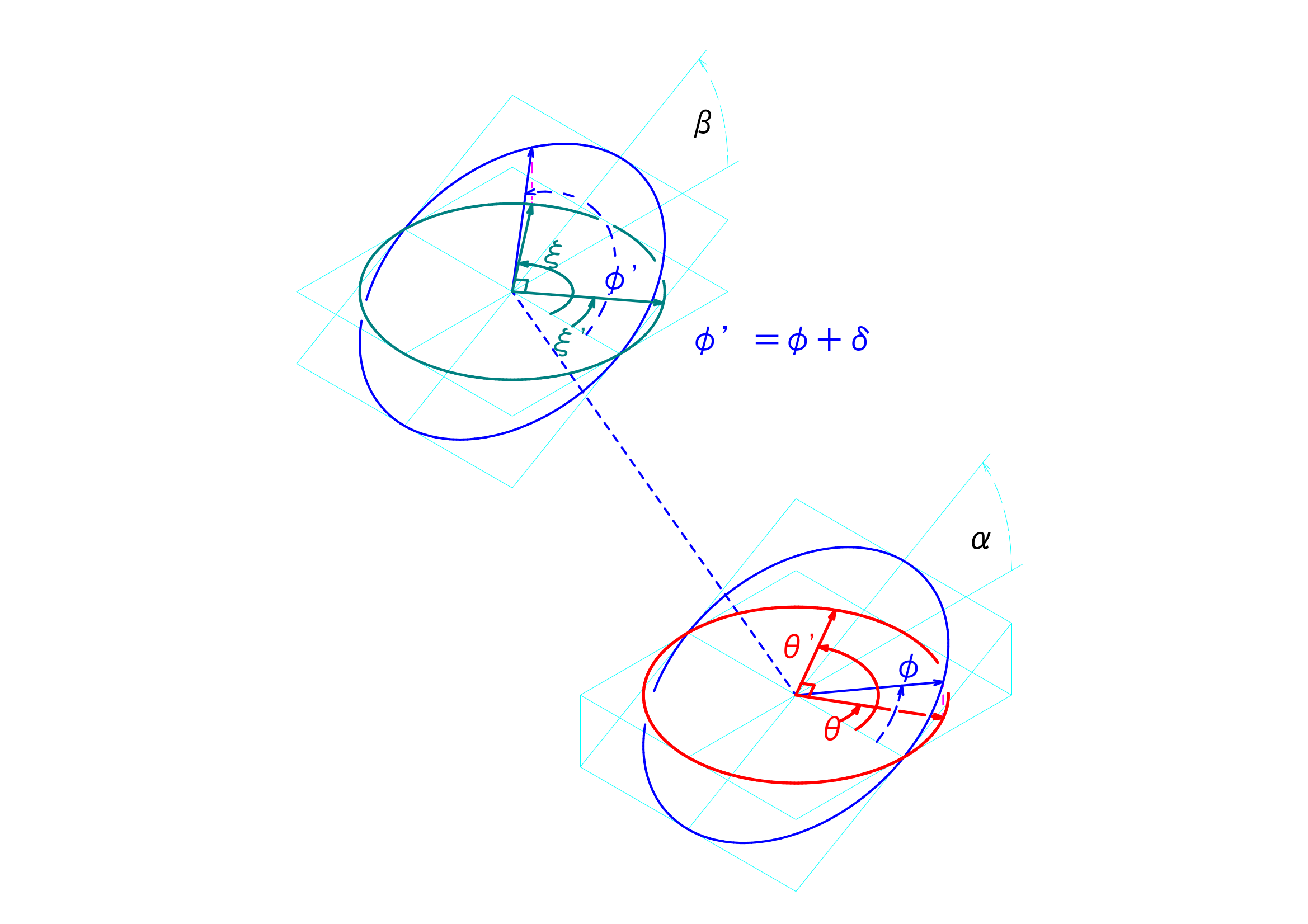
この式の変形が意味する事は、簡易型ユニバーサルジョイントの解析に用いた基準点の取り方を工夫すれば、正規型ユニバーサルジョイントと同じ式が導出できた、ということです。簡易型ユニバーサルジョイントを２つ組み合わせたときの図に\(\theta^\prime\)と\(\xi^\prime\)とを加えたのが下図です。

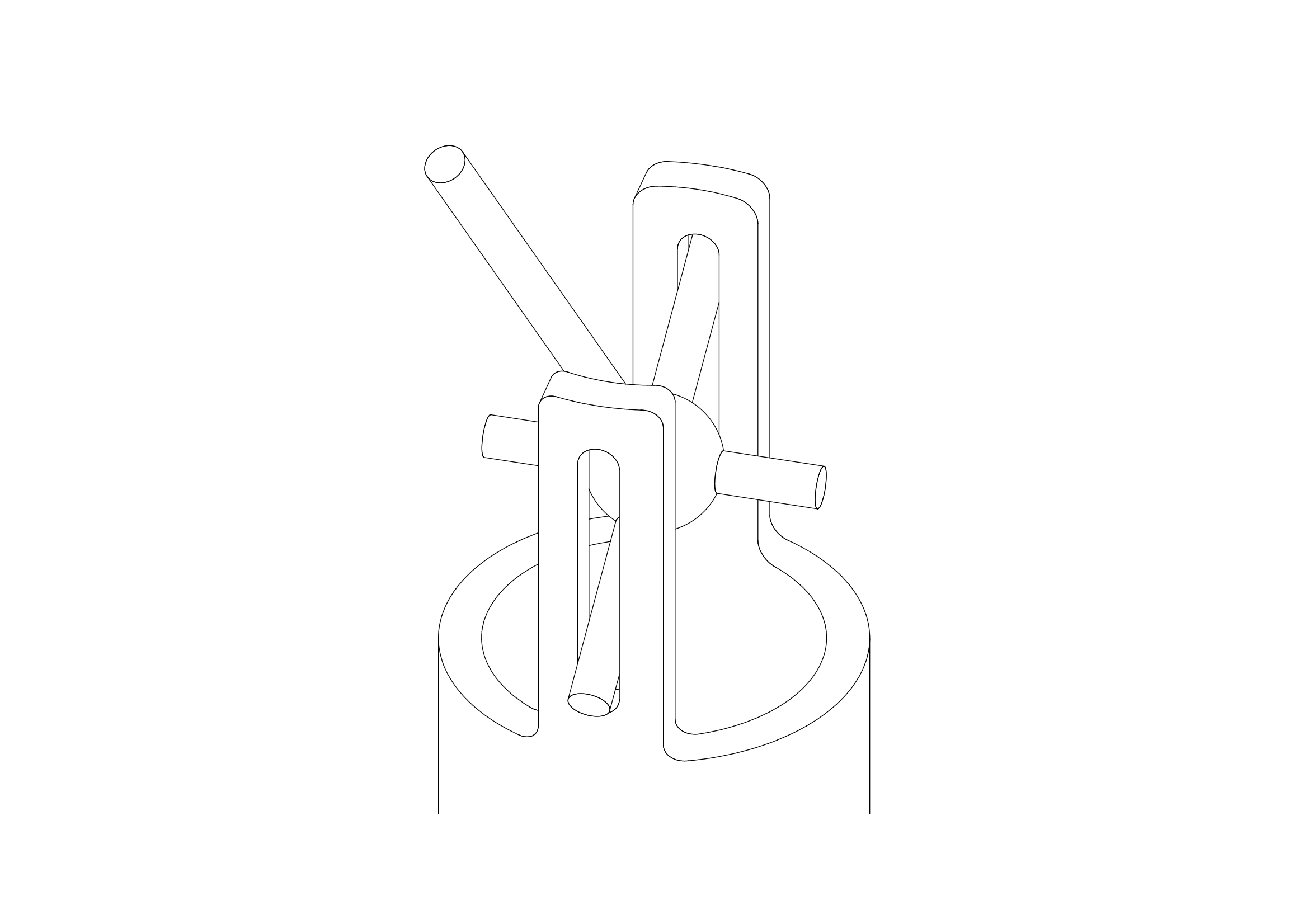
これはどういうことかというと、簡易型ユニバーサルジョイントに、下図のようなピンに垂直な仮想的な補助ピンを加え、その先端を基準点の一つとすればよい、ということを言っています。

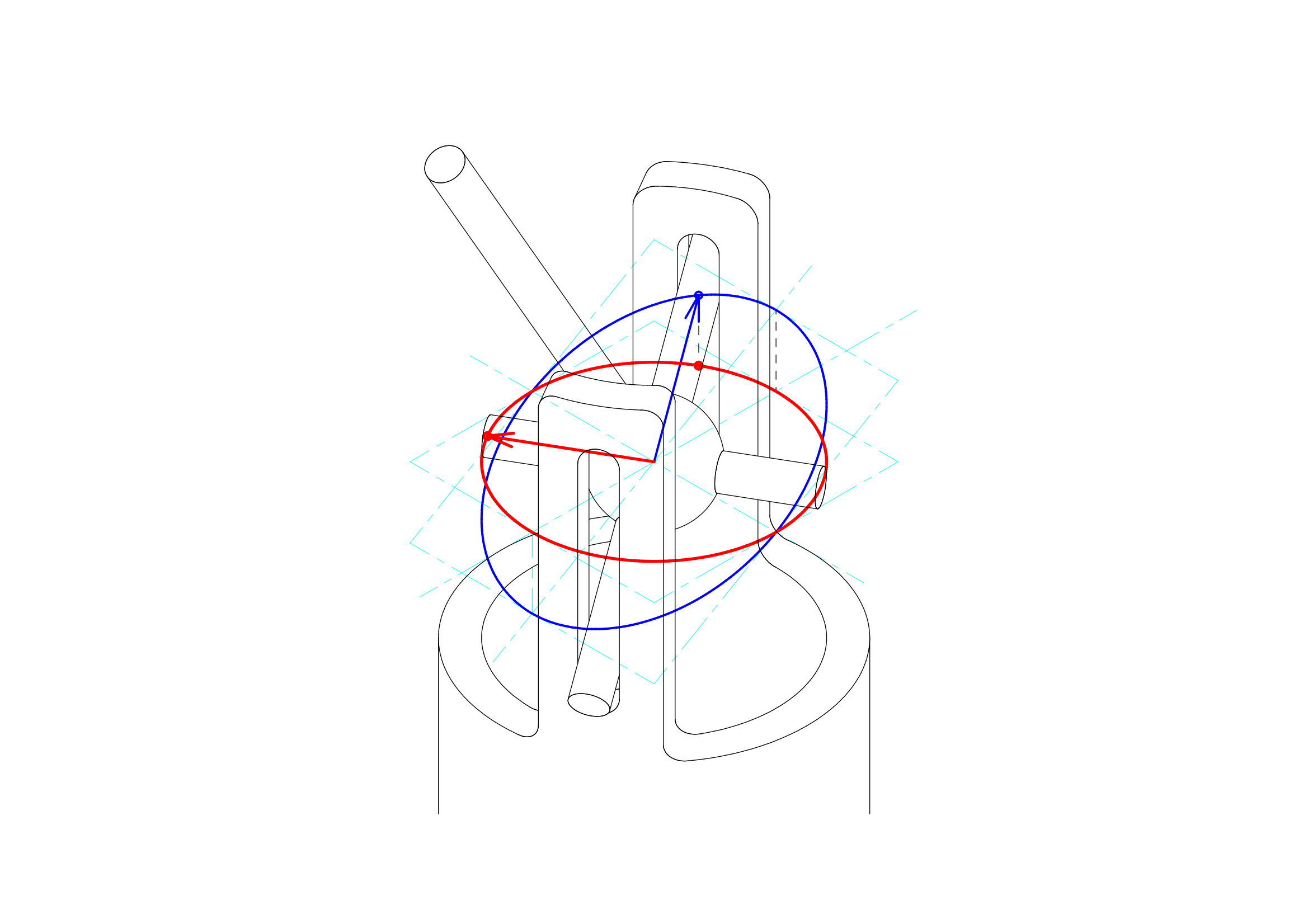
上図にて基準点示したのが下図となります。同一の垂直線上にある赤い点と青い点が簡易型ユニバーサルジョイントの解析をする際に用いた基準点に、仮想的な補助ピンの基準点を描き加えています。この仮想的な補助ピンの赤の基準点と青の基準点とを使って正規型のユニバーサルジョイントと同様の解析を進めることで、最終的には全く同じ結果が得られます。

ここまでの議論で、「簡易型ユニバーサルジョイントは、正規型ユニバーサルジョイントと等価である」ということがわかります。