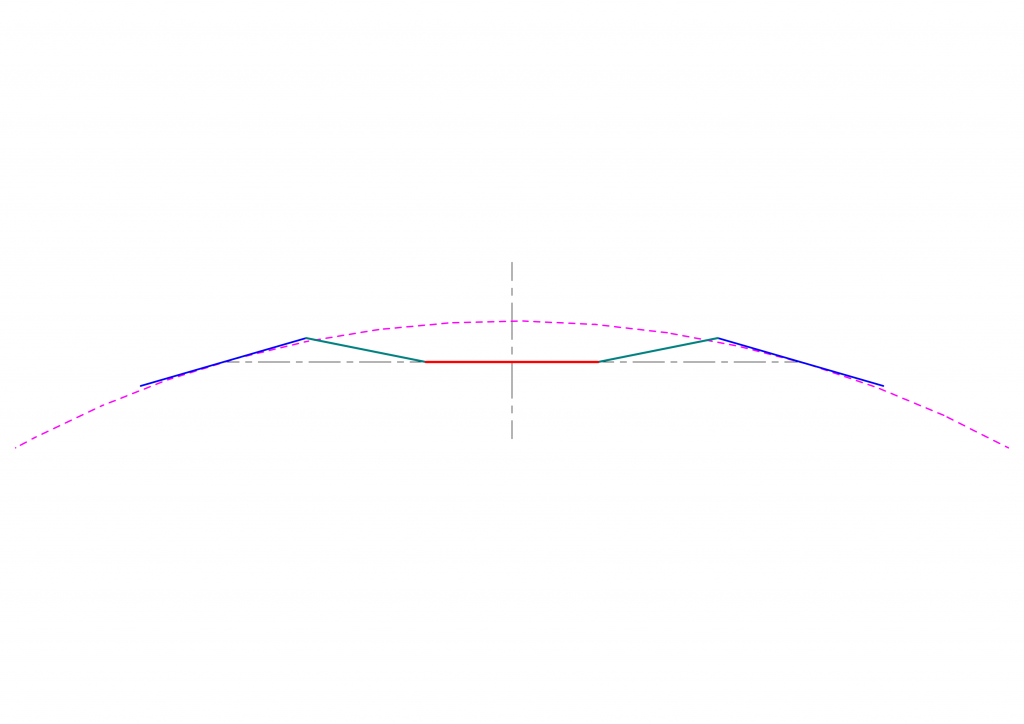
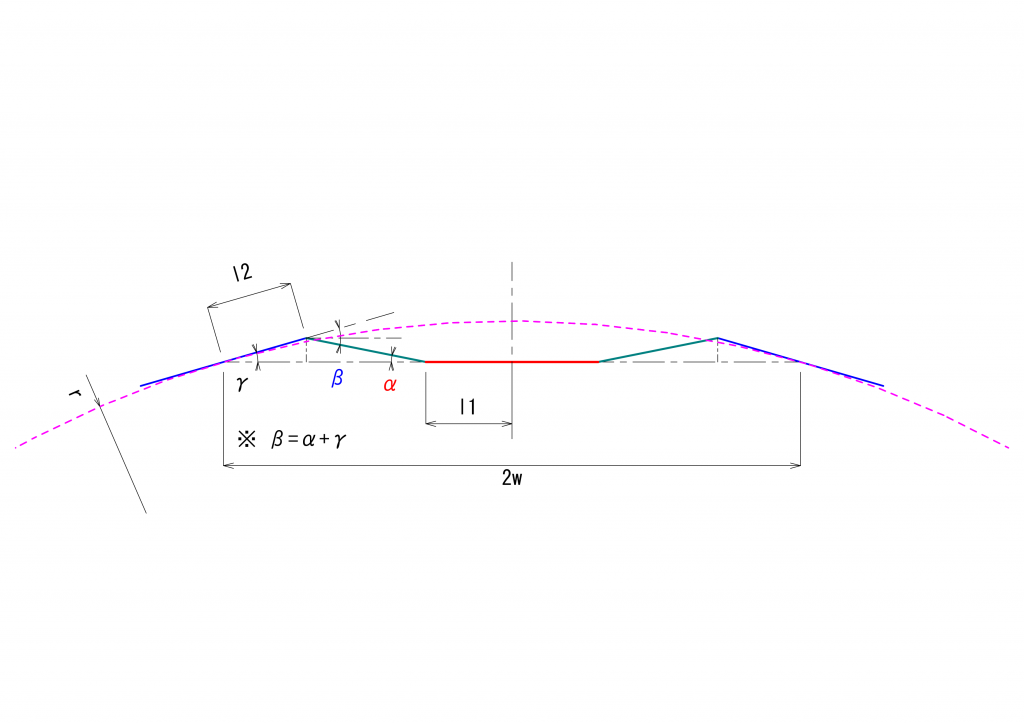
前回の議論で、MPギアに代表されるような、模型で一般的に使われる伝動機構での\(\alpha\)と\(\beta\)との関係を求めました。復習すると、下のような円弧上の曲線を走行している車両があった場合、

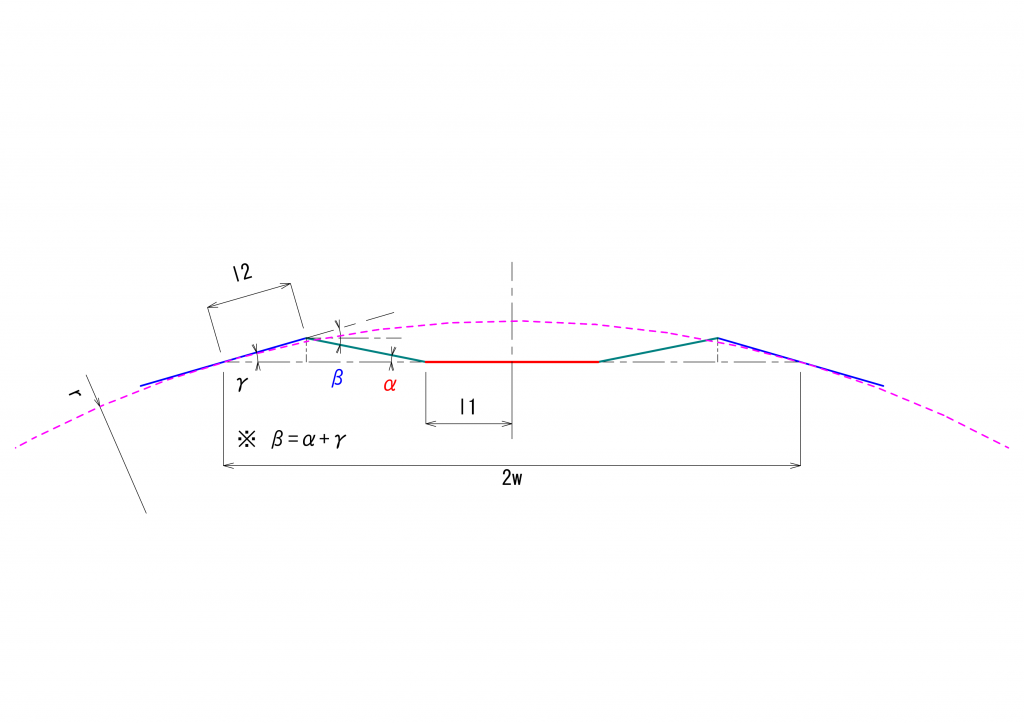
\(\alpha\)、\(\beta\)は、\(l_1\)、\(l_2\)、\(w\)、\(r\)から、次の順序で計算して求める事ができます。なお、電車の場合、通常は左右に駆動系を構成できると思いますので、以下の議論では、上図の左側のみを議論の対象とします。

\(\gamma = \frac{\pi}{2}-cos^{-1}(\frac{w}{r})\)

\(\alpha = tan^{-1}(\frac{l_2\cdot sin(\gamma)}{w – l_2\cdot cos(\gamma) – l_1})\)

\(\beta = \alpha + \gamma\)

また、以前の議論で、駆動面の角速度\(\omega\)が与えられたときに、\(\omega\)に対する最終伝達面の角速度の比は、以下で表されることを導き出しました。

伝達面と中継面との位相が揃っている(\(\delta=0\))の場合は

\(\frac{cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)\cdot cos^2(\beta) + sin^2(\omega t)\cdot cos^2(\alpha)}\)

伝達面と中継面との位相が90度ずれている(\(\delta=\frac{\pi}{2}\))の場合は

\(\frac{cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha)\cdot cos^2(\beta)}\)

これらの式から、\(w\)、\(l_1\)、\(l_2\)、\(r\)の値を当てはめれば角速度比がどう変動するかを求めることができます。あいにく私はMPギアを持った車両を持ち合わせていませんので、むすこたかなしさんにお願いして\(w\)、\(l_1\)、\(l_2\)の値を測っていただきました。この場を借りて御礼申し上げます。併せてわかりやすい写真もご提供いただきましたので、ありがたく使わせていただきます。

これが小田急8000系の実測値です。

\(l_1=27.7mm\)、\(l_2=26.4mm\)、\(w=85mm\)として、\(r=500mm\)の場合と、\(r=600mm\)の場合の角速度の変動をグラフ化したのが下です。

さらに、お持ちの国鉄の185系の寸法も測っていただきました。

同様に、\(l_1=34.0mm\)、\(l_2=24.5mm\)、\(w=87.5mm\)として、\(r=500mm\)の場合と、\(r=600mm\)の場合をグラフにしたのが下です。

2021/1/27追記: 下記の仮説は「ユニバーサルジョイントの使い方（２７）ーMPギアの左右の角速度の差について」で考察したとおり一旦取り下げます。

<ここから>

以前、dda40xさんのBlogで、nao sekiさんから、以下のコメントをいただきました。貴重な情報をいただいたnao sekiさんには改めて御礼申し上げます。

「カツミ製2014年製の165系キット組でエンドウ製ユニバーサルジョイント(6501)を対称組にしたところ、今まではR600くらいから鳴っていたものが、篠原製6番カーブポイント(R508)でもほとんど鳴ることはありませんでした。」

同じ国鉄型であるということで、nao sekiさんのお持ちの車両が上記の185系の寸法に準じており、R600で鳴っていたものがR508でもほとんど鳴らなくなったのが角速度の変動に起因している、と仮定すると、角速度の変動率が5%に近づくあたりから、スムーズな走行に影響を与える、という仮説を立てることができます。正確には、R600で位相が揃っていない場合の角速度の変動率は±4.47%、R508で位相が揃っている場合の角速度の変動率は±4.13%となります。

本来であれば自分で実験してこの仮説を検証できれば良いのでしょうが、残念ながらそういう環境にはないので、将来そのような環境が整うことがあればチャンレジしてみたいと思います。

<ここまで>

さて、上記の2つのグラフから以下のことが言えると思います。まずは、2つのグラフに共通していることとして、1) 位相がずれている(\(\delta=\frac{\pi}{2}\))の場合、位相が揃っている(\(\delta=0\))の場合に比べて、角速度比の変動が大きいこと、2) 位相がずれている場合は、曲線半径が小さくなった場合の角速度比の変動の増加の割合が大きいこと、の2つが言えると思います。

また、2つのグラフを比べると、\(l_1\)が長くなることで、角速度比の変動が大きくなることがわかります。\(l_2\)は実物の台車のホイールベースに制約され自由度がほとんどないことを考えると、\(l_1\)をなるべく短くすることが肝要と思います。また、最初にMPギアの駆動系の構成は左右対称として考えるという仮定を置きましたが、線分\(oa_1\)の長さと線分\(oa_2\)の長さとが異なるような配置はモーターの左右で角速度の変化率が異なることになりますので、避けるべきということも言えると思います。

参考までに、上記のモハ185の場合において、\(l_1\)が角速度の変動に与える影響をグラフにしてみました。位相が揃っている場合、\(l_1\)が長くなっても角速度の変動は穏やかであるのに対し、位相が揃っていない場合、\(l_1\)が少し長くなるだけで角速度の変動に大きな影響を与えることが読み取れます。

ここまでの結論をまとめると、

• ユニバーサルジョイントは必ず同位相とすること。
• 角速度の変動率が±5%に近づくあたりから、走行のスムーズさに影響を与える可能性があること。 (2021/1/27追記: 上記の通り、この仮説は取り下げます）
• モーターは可能な限り短いものとし、必ず中央に置くこと、モーターに装着するユニバーサルジョイントの位置はできる限り中央に近い位置に置くこと。

といったことが言えるかと思います。

随分と間が空いてしまいました。きわめて忙しかったこともあるのですが、この2回後に書きたいと思っている内容をうまくまとめることできず、考え込んでいたのもあります。もう忘れ去られているかもしれませんが、これまでの議論の続きを行います。

前回は\(|\alpha|=|\beta|\)となるような \(\alpha\)と\(\beta\)との関係を考えました。端的に言うと、\(|\alpha|=|\beta|\)となるような機構を模型において実現するのは容易ではなく、\(|\alpha|\ne|\beta|\)となる状況が発生することを念頭に置かなければならない、ということです。

今回は模型で一般的に使われると思われる機構において、\(\alpha\)と\(\beta\)とが、どのような関係となるかを考察してみたいと思います。下記は、dda40xさんのblogで紹介された機構です(商品名は、エンドウのMPギア)。なお、写真はdda40xさんのblogから拝借しています。

この機構では、カーブでの台車の回転に伴って左側のC点が回転し、右側のC点との間が伸び縮みします。

以下の議論を進めるために、この機構を持った車両が円弧上を走行している状態を下図のようにモデル化します。二本の線路の中心の円弧を紫の点線が、上の写真の左側のC点から車体の端より（左側）に位置するモーターからの駆動力を車輪に伝える軸を青い実線が表します。赤の実線は上の写真の右側のC点から車体中央寄りののC点から車体中心より（右側）のモーターの軸を表し、これは車体に対して固定されています。緑の実線が2つのC点の間をつなぐBのパーツに相当し、カーブ走行時に伸縮します。

これらの位置関係を数式で表してゆきます。まず、走行中の曲線の半径を\(r\)とします。\(o\)は車体の中心の位置を、\(c_1\)、\(c_2\)は台車の中心の位置を表します。\(a_1\)、\(a_2\)は、モーター側のユニバーサルジョイントの中心の位置を、\(b_1\)、\(b_2\)は、台車側のユニバーサルジョイント中心の位置を示します。\(c_1\)、\(a_1\)、\(o\)、\(a_2\)、\(c_2\)を通る直線に対して、\(b_1\)、\(b_2\)から 垂直に線を引いたときにこの直線と交わる点をそれぞれ\(d_1\)、\(d_2\)とします。

\(c_1\)と\(c_2\)の距離、つまり線分\(c_1c_2\)の長さ、を\(2\cdot w\)とします。\(o\)は\(c_1c_2\)の中心となりますので、線分\(oc_1\)の長さは、\(w\)となります。線分\(oa_1\)の長さを\(l_1\)、線分\(b_1c_1\)の長さを\(l_2\)とします。

実際に台車が曲線でどれだけ回転するかを厳密に求めるのは簡単ではないと思いますので、\(b_1c_1\) は、半径\(r\)の曲線に\(c_1\)において接するという仮定を置きます。言い換えると、\(c_1\)は半径\(r\)の円の上にある点であり、かつ、\(c_1\)とこの円との中心\(O_r\)（注：上の図には示していません）とを結んだ線は \(b_1c_1\) と直交します。

また、\(a_1d_1\)と\(a_1b_1\)のなす角度を\(\alpha\)、\(c_1b_1\)を車体中心方向（右）に延長した線と\(b_1a_1\)とのなす角度を\(\beta\)、\(c_1d_1\)と\(c_1b_1\)のなす角度を\(\gamma\)、とします。

半径\(r\)の円弧の中心\(O_r\)と\(c_1\)、\(c_2\)とがなす三角形は、二等辺三角形となり、その底角は\(\frac{\pi}{2}-\gamma\)となります。また、底辺の\(c_1c_2\)の長さは\(2\cdot w\)、等辺\(O_rc_1\)、\(O_rc_2\)の長さは\(r\)となりますので、三角関数の定義から、

\(\frac{w}{r}=cos(\frac{\pi}{2}-\gamma)\)

が成立します。

\(b_1\)、\(c_1\)、 \(d_1\) がなす直角三角形に注目すると、線分\(c_1d_1\)の長さは\(l_2\cdot cos(\gamma)\)、線分\(b_1d_1\)の長さは\(l_2\cdot sin(\gamma)\)、であることが三角関数の定義から導けます。

\(b_1\)、\(d_1\)、\(a_1\)がなす直角三角形に注目します。線分\(a_1d_1\)の長さは、線分\(oc_1\)の長さから、上で求めた線分\(c_1d_1\)の長さ\(l_2\cdot cos(\gamma)\)と、線分\(oa_1\)の長さである\(l_1\)を引いた、\(w-l_1-l_2\cdot cos(\gamma)\)となります。線分\(b_1d_1\)の長さは上で求めた\(l_2\cdot sin(\gamma)\)でしたので、

\(tan(\alpha) = \frac{l_2\cdot sin(\gamma)}{w – l_2\cdot cos(\gamma) – l_1}\)

が成立します。

また、２つの平行な線に交わる線を引いたときの錯角、同位角の関係から、\(b_1\)を起点に\(c_1o\)に平行な補助線を引くと、\(\beta = \alpha + \gamma\)が成立することがわかります。

これまでの議論をまとめると\(\alpha\)、\(\beta\)を求めるには、

\(\gamma = \frac{\pi}{2}-{cos}^{-1}(\frac{w}{r})\)

\(\alpha = {tan}^{-1}(\frac{l_2\cdot sin(\gamma)}{w – l_2\cdot cos(\gamma) – l_1})\)

\(\beta = \alpha + \gamma\)

を順に計算すればよいことがわかります。

この式から確認できることは、MPギアでは、曲線に入ると、\(|\alpha|\ne|\beta|\)という状況が発生する、つまり、台車を駆動する側の軸では、角速度の変動が必ず発生する、ということです。

次回は実際にいくつかの数値を当てはめて考察を進めます。