2020/8/30追記。 Tavataさんにいただいたコメントを参考に追記しました。
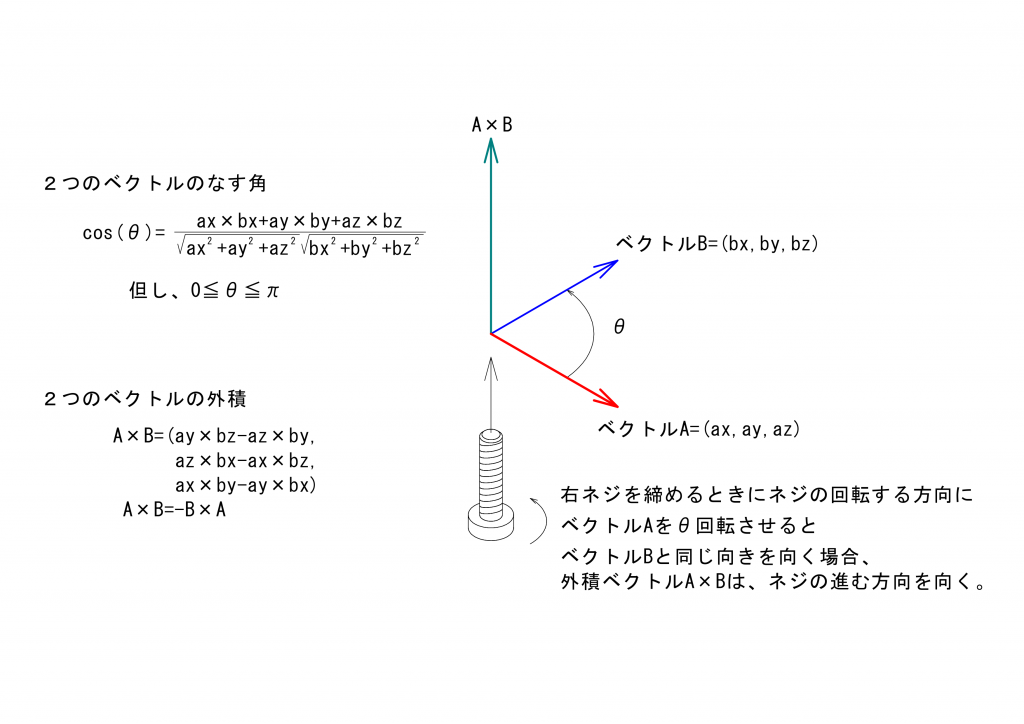
前回説明した2つのベクトルのなす角度および外積を利用し、3つの軸が同一平面上にないユニバーサルジョイントの解析に必要となる\(\alpha\)、\(\beta\)、\(\eta\)の計算方法を考察してゆきます。
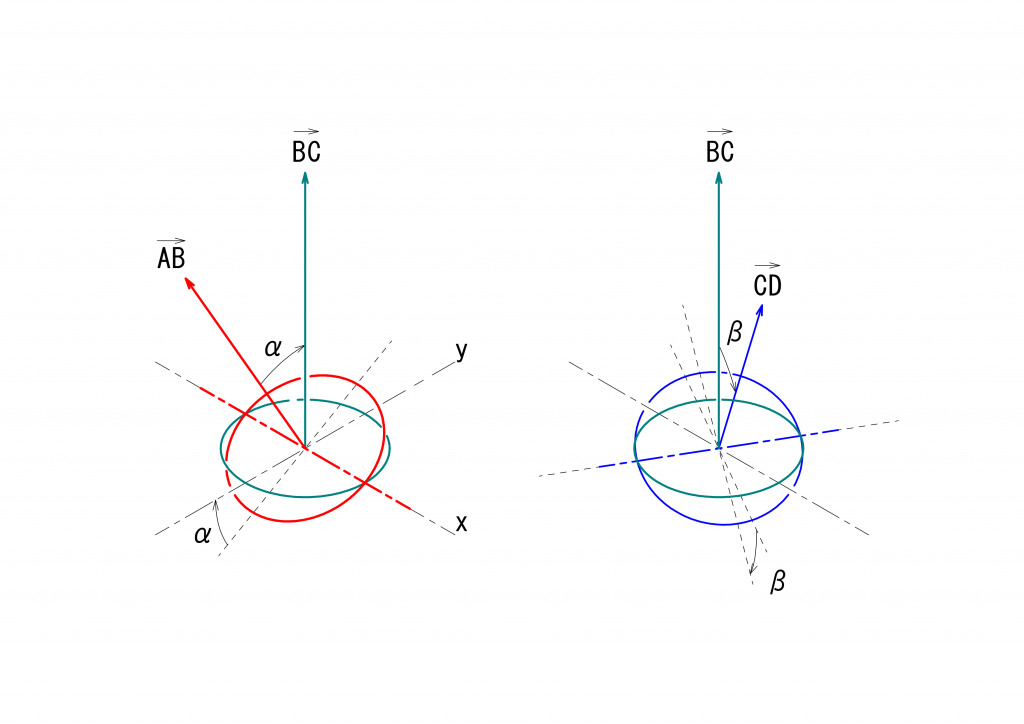
以前示した図ですが、ユニバーサルジョイントは3つの軸で構成され、4つの点\(A\)、\(B\)、\(C\)、\(D\)で規定されます。軸\(AB\)が軸\(BC\)に動力を伝え、軸\(BC\)が軸\(CD\)に動力を伝えるものとします。
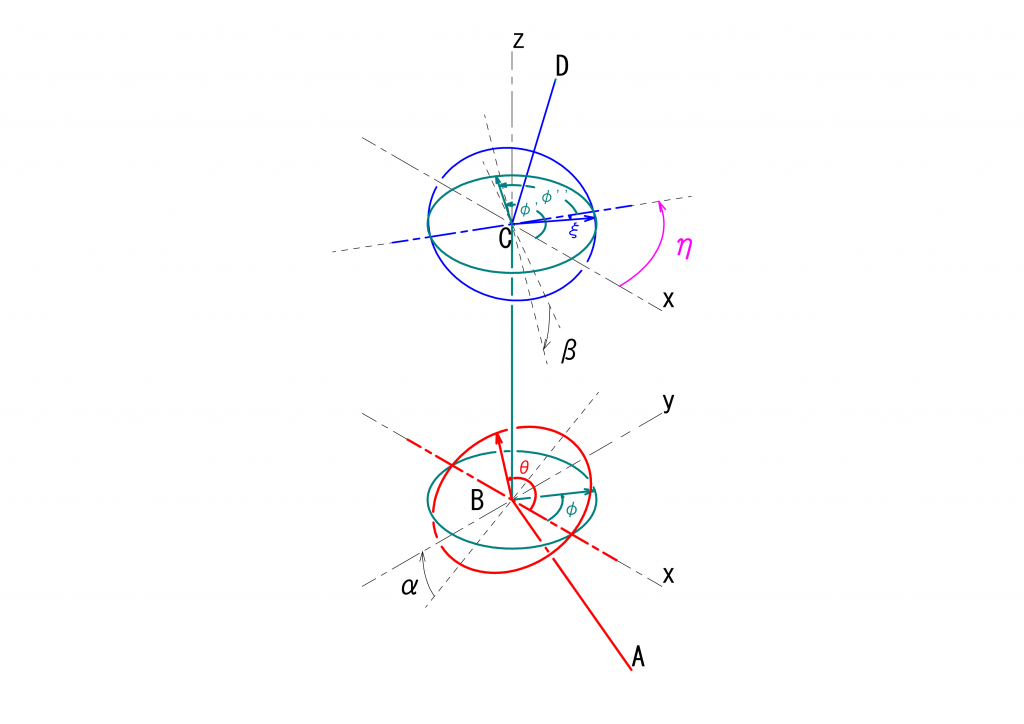
このとき、\(B\)を通り\(AB\)に垂直な赤い円を含む平面が駆動面、\(B\)を通り\(BC\)に垂直な緑の円を含む平面が伝達面、となります。駆動面に対する伝達面の傾き\(\alpha\)は、ベクトル\(\vec{AB}\)とベクトル\(\vec{BC}\)とのなす角度として求めることができます。
\(cos(\alpha)=\frac{\vec{AB}\cdot\vec{BC}}{|\vec{AB}|\cdot|\vec{BC}|}\)
同じ議論が中継面と最終伝達面に関しても成り立ちます。\(C\)を通り\(BC\)に垂直な緑の円を含む平面が中継面、\(C\)を通り\(CD\)に垂直な青い円を含む平面が最終伝達面、となります。ベクトル\(\vec{BC}\)とベクトル\(\vec{CD}\)とのなす角度が中継面に対する最終伝達面の傾き\(\beta\)となります。
\(cos(\beta)=\frac{\vec{BC}\cdot\vec{CD}}{|\vec{BC}|\cdot|\vec{CD}|}\)
これらの4つのベクトルと、\(\alpha\)、\(\beta\)の関係を念のために次に示します。
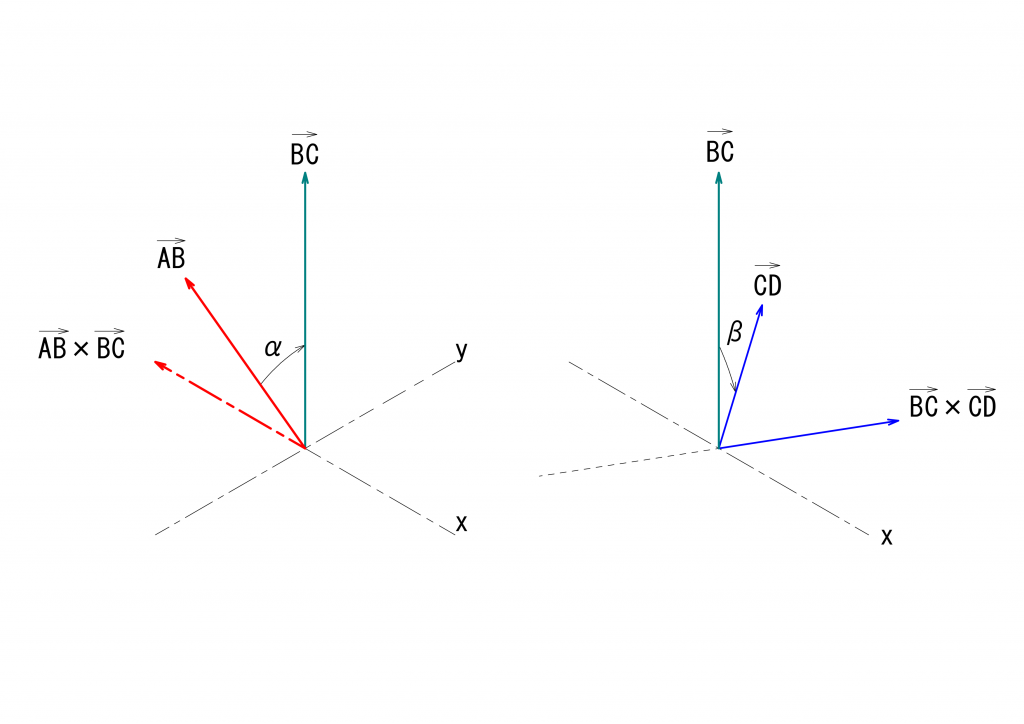
次に\(\eta\)を求めます。これは、駆動面および伝達面を回転する点の回転角の基準となる線(赤の一点鎖線)に対して、中継面と最終伝達面を回転する点の回転角の基準となる線(青の一点鎖線)がどれだけ回転しているかを表す角度です。
駆動面および伝達面を回転する点の回転角の基準となる線は\(AB\)および\(BC\)に垂直であることを思い出せば、\(\vec{AB}\)と\(\vec{BC}\)の外積\(\vec{AB}\times\vec{BC}\)を基準線として利用することができます。同様に、中継面と最終伝達面を回転する点の回転角の基準となる線として、\(\vec{BC}\)と\(\vec{CD}\)との外積\(\vec{BC}\times\vec{CD}\)を利用することができます。
これらの関係を下の図に示します。なお、今回の議論ではベクトルの外積の向きにだけ興味がありますので、ベクトルの大きさは必ずしも正しくありません。
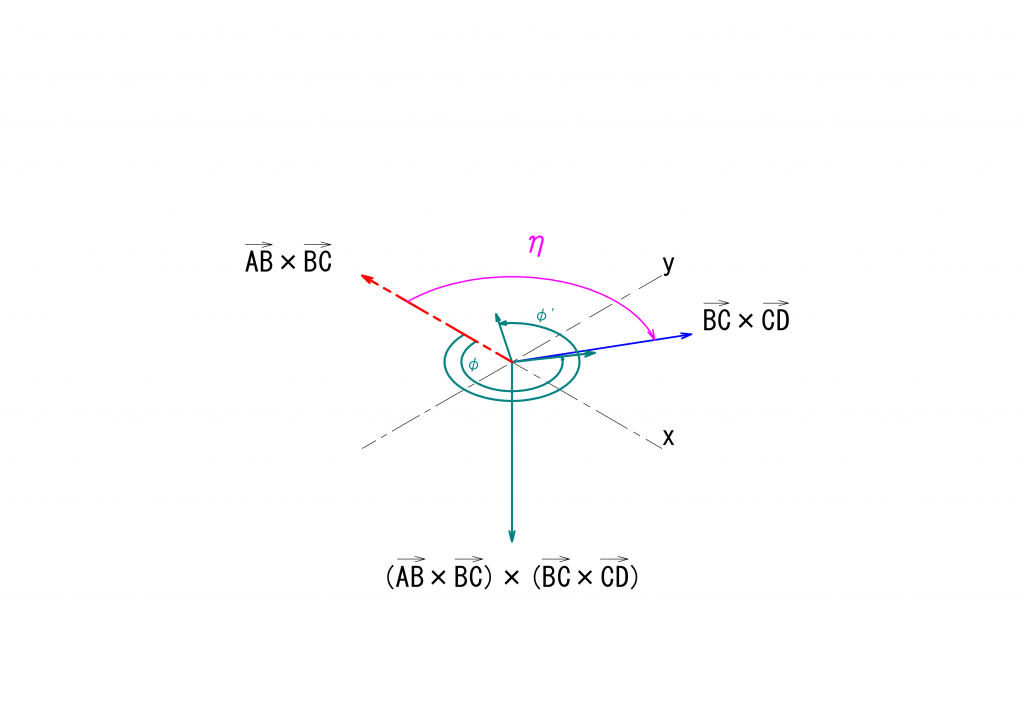
\(\eta\)を求めるには、\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta_{abs}\)を求め、\(\vec{AB}\times\vec{BA}\)に対する\(\vec{BC}\times\vec{CD}\)の回転方向に応じて符号を与えることが必要です。
まず、\(\eta_{abs}\)は次の式を使って求める事ができます。
\(cos(\eta_{abs})=\frac{(\vec{AB}\times\vec{BC})\cdot(\vec{BC}\times\vec{CD})}{|\vec{AB}\times\vec{BC}|\cdot|\vec{BC}\times\vec{CD}|}\)
\(BC\)と垂直な2つのベクトル\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)の外積ベクトル\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)を求めると、\(\vec{BC}\)か\(\vec{CB}\)かのいずれかと同じ向きを向くベクトルとなります。
\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)と\(\vec{BC}\)との内積が、正、負に応じて、\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)はそれぞれ、\(\vec{BC}\)、\(\vec{CB}\)と同じ向きとなります。
\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)が\(\vec{BC}\)と同じ方向の場合、\(\vec{BC}\)の方向にネジを締める向きに\(\vec{AB}\times\vec{BA}\)を回転すれば、\(\vec{BC}\times\vec{CD}\)と同じ向きとなりますので、\(\eta=\eta_{abs}\)とします。さもなくば、\(\eta=-\eta_{abs}\)とします。
2つのベクトルが同じ向きかを調べる方法はいくつか考えられますが、ここでは以下の方法をとります。
2つのベクトルが同じ向き(反対向き)の場合は、2つのベクトルのなす角は\(0\)(\(\pi\))となり、そのなす角の余弦(\(cos\))は1(-1)となります。2つのベクトルの内積を、2つのベクトルの長さの積で割ったものは、2つのベクトルのなす角の余弦(\(cos\))となることを思い出せば、
\(\eta=\eta_{abs}\cdot\frac{((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD}))\cdot\vec{BC}}{|(\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})|\cdot|\vec{BC}|}\)
となります。
最初に示した図の場合では、\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)は\(\vec{CB}\)と同じ向きを向きますので、\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta_{abs}\)に\(-1\)をかけたものが\(\eta\)となります。
これを図示したのが下となります。この時、中継面の基準点の角度\(\varphi’\)と最終伝達面の基準点の角度\(\xi\)との間の関係式は、次のようになります。
\(tan(\xi) = -\frac{1}{tan(\varphi’-(-\eta))}\cdot\frac{1}{cos(\beta)}\)
最初に示した図からは、次のような図を連想するかと思いますが、上の図とは随分と様子が異なります。これはどういうことでしょうか。
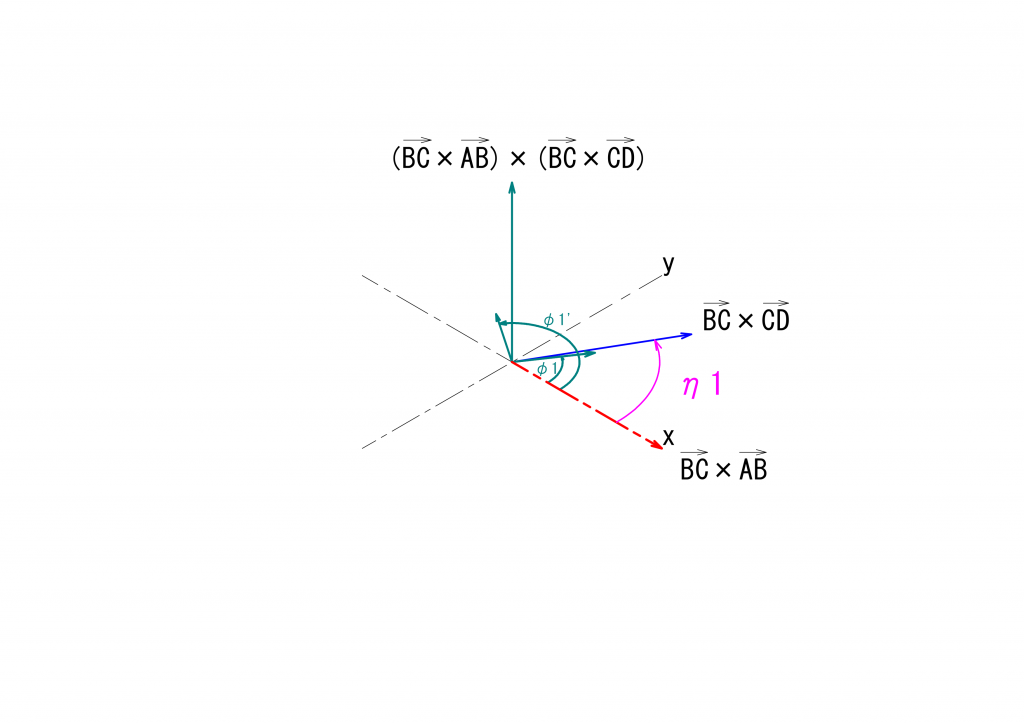
この図では、中継面の基準点の角度\({\varphi_1}’\)と最終伝達面の基準点の角度\(\xi\)との間には次の関係が成り立ちます。
\(tan(\xi) = -\frac{1}{tan({\varphi_1}’-\eta_1)}\cdot\frac{1}{cos(\beta)}\)
\({\varphi_1}’=\varphi’-\pi\)、\(\eta_1=\pi-\eta\)ですので、これを上の式に代入すると、
\(tan(\xi) = -\frac{1}{tan(\varphi’-2\pi-\eta)}\cdot\frac{1}{cos(\beta)}\)
となります。三角関数の周期性から\(tan(\theta-\pi) = tan(\theta)\)ですので、この式は
\(tan(\xi) = -\frac{1}{tan(\varphi’-\eta)}\cdot\frac{1}{cos(\beta)}\)
となり、先ほど図の説明で示した式そのものです。つまり、上の2つの図は見た目は異なりますが、実は全く同じ計算をしていることになります。
あるいは直感的には、\(\vec{BC}\times\vec{CD}\)を起点に、反時計回りに\(\eta\)と\(\varphi’\)の角度の和の\(tan\)を求めるわけですが、これが一回り以上していますので、その一回り分の\(2\pi\)を差し引くというのが、\(tan(\varphi’-\eta-2\pi)\)という式に表れてくる、と考えることもできます。
ユニバーサルジョイントの3つの軸が同一平面にある場合は、作図によって、わかりやすい方向を人間が考えて式をたてることができました。3つの軸が同一平面にない場合は、ここで説明したようなベクトルの演算で解析を行いました。ベクトルの向きを厳密にしかし一貫性のあるように、扱うことになったと言えます。
念のため今までの議論による計算方法を示します。これまでの議論をもとに、計算に集中できるようにした式ですので、冗長な記述となっている点をご了解ください。
まず、\(A\)、\(B\)、\(C\)、\(D\)の座標をそれぞれ\(A=(a_x,a_y,a_z)\)、\(B=(b_x,b_y,b_z)\)、\(C=(c_x,c_y,c_z)\)、\(D=(d_x,d_y,d_z)\)とします。原点をどのように設定しても結果は変わりませんので、考えやすい点を原点として座標を決めれば大丈夫です。
すると、
\(\vec{AB}=(b_x-a_x, b_y-a_y, b_z-a_z)\)
\(\vec{BC}=(c_x-b_x, c_y-b_y, c_z-b_z)\)
\(\vec{CD}=(d_x-c_x, d_y-c_y, d_z-c_z)\)
となります。式が複雑になるので、以下
\(\vec{AB}=(b_x-a_x, b_y-a_y, b_z-a_z)=(ab_x, ab_y,ab_z)\)
\(\vec{BC}=(c_x-b_x, c_y-b_y, c_z-b_z)=(bc_x,bc_y,bc_z)\)
\(\vec{CD}=(d_x-c_x, c_y-c_y, d_z-c_z)=(cd_x,cd_y,cd_z)\)
と置きます。
\(\alpha\)、\(\beta\)はこれらから
\(\alpha=cos^{-1}(\frac{ab_x\cdot bc_x+ab_y\cdot bc_y+ab_z\cdot bc_z}{\sqrt{{ab_x}^2+ {ab_y}^2+ {ab_z}^2}\cdot\sqrt{{bc_x}^2+ {bc_y}^2+ {bc_z}^2}})\)
\( \beta=cos^{-1}(\frac{bc_x\cdot cd_x+bc_y\cdot cd_y+bc_z\cdot cd_z}{\sqrt{{bc_x}^2+ {bc_y}^2+ {bc_z}^2}\cdot\sqrt{{cd_x}^2+ {cd_y}^2+ {cd_z}^2}})\)
と求めることができます。
次に、\(\vec{AB}\)と\(\vec{BC}\)との外積、\(\vec{BC}\)と\(\vec{CD}\)との外積、を求めます。
\(\vec{AB}\times\vec{BC} = (ab_y\cdot bc_z-ab_z\cdot bc_y, ab_z\cdot bc_x-ab_x\cdot bc_z, ab_x\cdot bc_y-ab_y\cdot bc_x)\)
\(\vec{BC}\times\vec{CD} = (bc_y\cdot cd_z-bc_z\cdot cd_y, bc_z\cdot cd_x-bc_x\cdot cd_z, bc_x\cdot cd_y-bc_y\cdot cd_x)\)
式が複雑にならないよう、
\(\vec{AB}\times\vec{BC} = (ab_y\cdot bc_z-ab_z\cdot bc_y, ab_z\cdot bc_x-ab_x\cdot bc_z, ab_x\cdot bc_y-ab_y\cdot bc_x)\)
\(=(abc_x,abc_y,abc_z)\)
\(\vec{BC}\times\vec{CD} = (bc_y\cdot cd_z-bc_z\cdot cd_y, bc_z\cdot cd_x-bc_x\cdot cd_z, bc_x\cdot cd_y-bc_y\cdot cd_x)\)
\(=(bcd_x,bcd_y,bcd_z)\)
と置きます。
すると、\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta\)の絶対値は、
\(|\eta| = cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)
となります。
\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)との外積は、次のように計算できます。
\((\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD}) = \)
\((abc_y\cdot bcd_z-abc_z\cdot bcd_y, abc_z\cdot bcd_x-abc_x\cdot bcd_z, abc_x\cdot bcd_y-abc_y\cdot bcd_x)\)
\(\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD})\)と\(\vec{BC}\)との内積を計算します。
\((\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD})\cdot\vec{BC}=\)
\(((abc_y\cdot bcd_z-abc_z\cdot bcd_y)\cdot bc_x,(abc_z\cdot bcd_x-abc_x\cdot bcd_z)\cdot bc_y, (abc_x\cdot bcd_y-abc_y\cdot bcd_x)\cdot bc_z)\)
先ほどはこの値を2つのベクトルの長さの積で割り、2つのベクトルの余弦を求めましたが、数値計算の誤差が出る場合があるので、上の値の符号で判定する方が現実的かと思います。
従って、上記の内積が正であれば、
\(\eta=cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)
上記の内積が負であれば、
\(\eta=-cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)
となります。
次回は、この結果を使って実際の数値を当てはめる予定です。