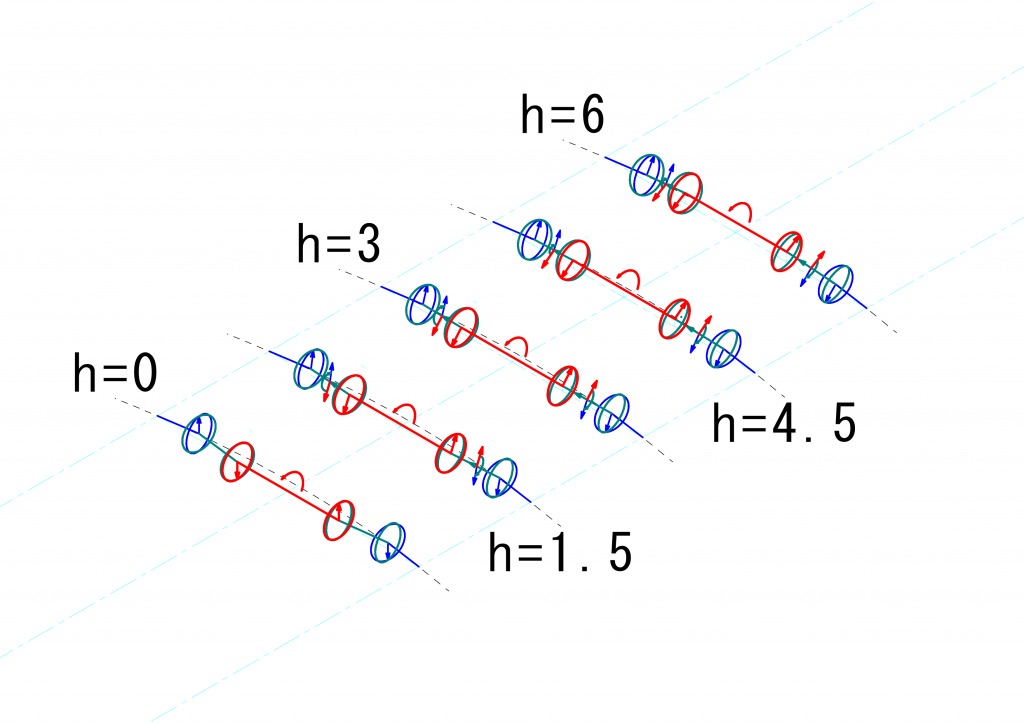
ユニバーサルジョイントの3つの軸が平面にない場合の角速度の変動を前回求めました。簡単におさらいすると、3つの軸が同一平面上にあり、駆動面の角速度を\(\omega\)としたときの最終伝達面の角速度

\(\frac{d\xi}{dt}= \frac{\omega\cdot cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

において、\(\delta\)を\(\delta-\eta\)で読み替えたものが、最終伝達面の角速度となります。

従って、駆動面の角速度に対する最終伝達面の角速度の比は、

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)

で求められます。

今回は、MPギアの場合を例にとり、モーターの軸が台車の軸に対し、\(0mm\)から\(6mm\)まで、\(1.5mm\)刻みで高さが変化したときに、角速度比がどのように変化するかを計算します。

MPギアでは、3つの軸が同一平面に置かれることを想定していると理解しており、ここでの議論そのものに意味はないかと思いますが、全体の傾向を把握するために結果を示すものです。

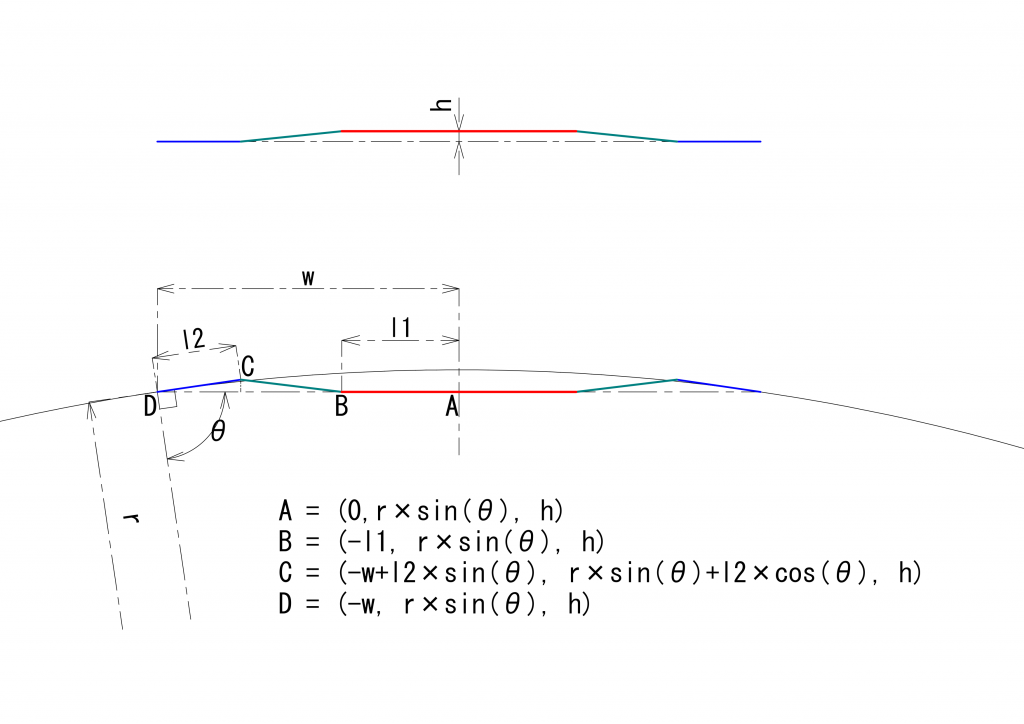
まず、下の図に座標の求め方を記しました。曲線の中心\(O_r\)を原点とすると、\(A\)、\(B\)、\(C\)、\(D\)は、次のように計算することができます。三角関数が理解できていれば簡単に導出できますので、詳しい説明は省略します。

\(A = (0,r\cdot sin(\theta), h)\)

\(B=(-l_1, r\cdot sin(\theta), h)\)

\(C=(-w+l_2\cdot sin(\theta), r\cdot sin(\theta)+l_2\cdot cos(\theta), h)\)

\(D=(-w, r\cdot sin(\theta), h)\)

以前示したエンドウのモハ185の寸法において、600Rで角速度比がどのように変動するかを示したのが次のグラフです。

R=500の場合を示します。

いずれのグラフを見ても、\(h\)が増えると、角速度の変動の比率が急激に大きくなること、逆位相の場合は特に顕著に大きくなること、が分ります。

これまで繰り返してきた、「ユニバーサルジョイントは必ず同位相で使うこと」、に加え、「ユニバーサルジョイントは必ず同一平面上に存在するように高さを調整すること」、が必要であると言えます。

最後に、\(h\)の変動に伴って、\(\eta\)がどのように変動するかの図を参考に示します。