前回は、3つの軸が同一平面に存在しない場合の角速度の変動を、MPギアの場合を例にとってまとめました。MPギアは、車体の中心で左右対称という構成となっていますので、モーターの左右にあるユニバーサルジョイントは同じ挙動を示すであろうということが想像できますが、この点について明確にしておきたいと思います。
まず、MPギアに使われるユニバーサルジョイントの座標を改めて次の図に示します。前回の図の\(A\)、\(B\)、\(C\)、\(D\)に加え、左右対称に\(A’\)、\(B’\)、\(C’\)、\(D’\)を示しました(ただし、\(A=A’\))。
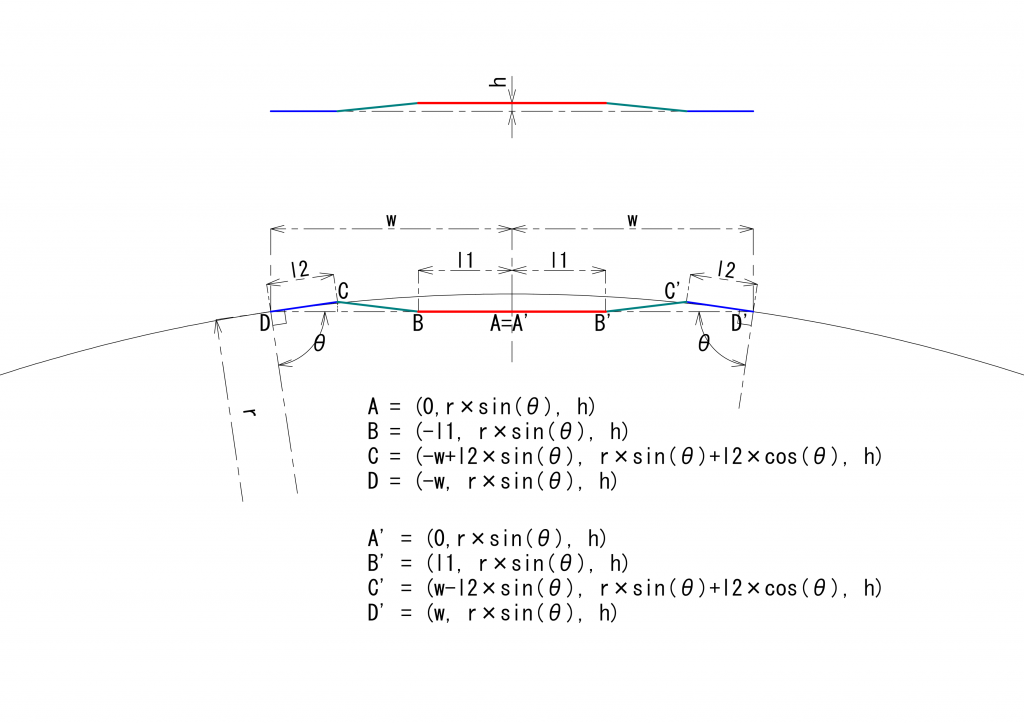
立体的に表現すると次のようになります。なお、この図を含めた以下の図は、ベクトルの角度および向きを示すことを目的としたものであり、ベクトルの長さは実際の値を反映したものではありません。
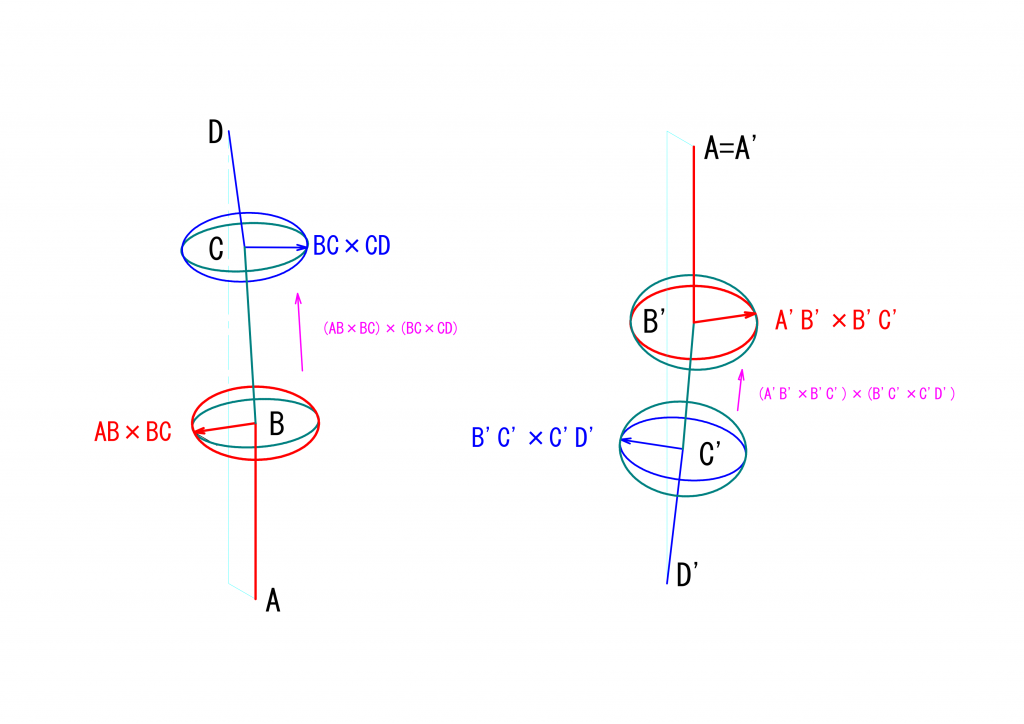
3つの軸が同一平面に存在しないユニバーサルジョイントの挙動を解析する際のポイントは、2つのベクトルのなす角と外積とを使って解析に必要な角度を求める、の記事で述べたように、\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta\)を求めることです。同様に\(\vec{A’B’}\times\vec{B’C’}\)と\(\vec{B’C’}\times\vec{C’D’}\)とのなす角\(\eta’\)を求めることで、モーターの左右にあるユニバーサルジョイントの挙動を解析することができます。これらを求めた結果の一例を次に図示します。
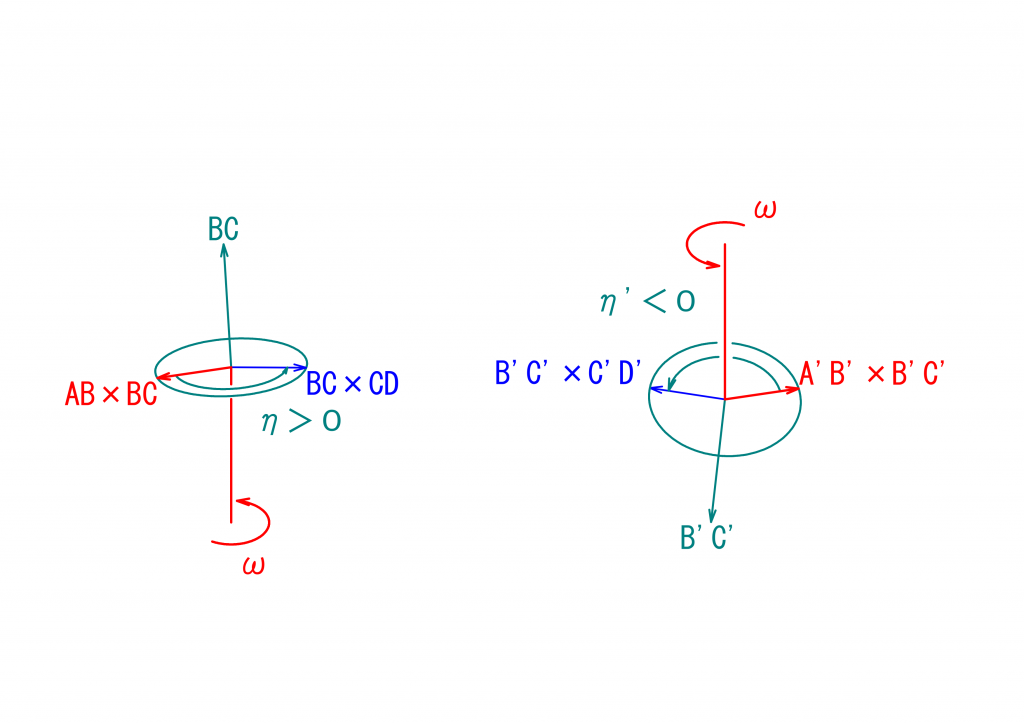
向きをそろえた図の方がわかりやすいと思いますので、これを下に示します。
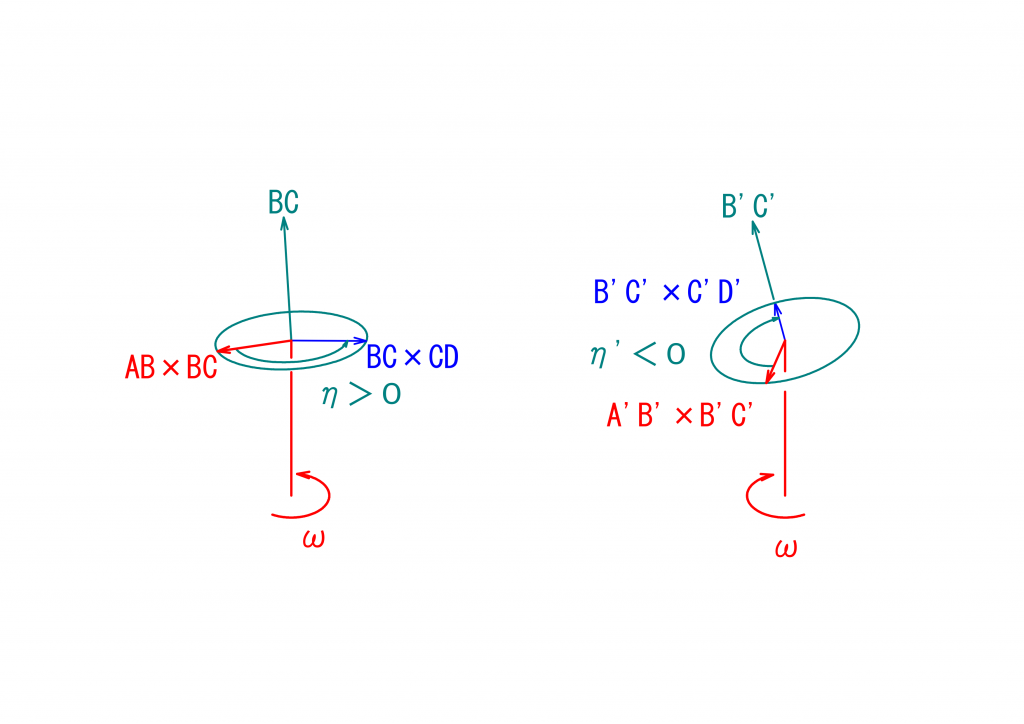
この図からわかることは、\(\eta\)と\(\eta’\)とは、絶対値は同じとなりますが、符号は異なる、ということです。更に軸の回転方向も反対となりますので、左側のユニバーサルジョイントの駆動面の角速度を\(\omega\)とすると、右側のユニバーサルジョイントの駆動面は\(-\omega\)として考える必要があります。
これらをもとに、以前示した、駆動面に対する最終伝達面の角速度の比が、左と右とでどうなるかを考えてみます。
ユニバーサルジョイントの駆動面に対する最終伝達面の角速度の比は、次の式で表すことができるのでした。
\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)
この式がモーターの左側のユニバーサルジョイントの最終伝達面の角速度の比を表すとすると、\(\omega\)と\(\eta\)との符号を反転させた式が右側のユニバーサルジョイントの最終伝達面の角速度の比を示す式となります。なお、\(\alpha\)、\(\beta\)については、絶対値のみを考えればよいことは以前に述べましたし、左右対称であることから、絶対値は一致しますので、以下の議論には影響を与えません。
\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(-\omega t)+{sin}^2(-\omega t)\cdot {cos}^2(\alpha) – (cos(-\omega t)\cdot cos(\delta-(-\eta))-sin(-\omega t)\cdot cos(\alpha)\cdot sin(\delta-(-\eta)))^2\cdot{sin}^2(\beta)}\)
\(sin(-\theta)=-sin(\theta)\)、\(cos(-\theta)=cos(\theta)\)ですので、上記の式は、
\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta+\eta))^2\cdot{sin}^2(\beta)}\)
となります。2つの式を見比べると、異なるのは分母の一部で、モーターの左側の角速度の比を示す式の
\(cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta)\)
と、モーターの右側の角速度の比を示す式の
\(cos(\omega t)\cdot cos(\delta+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta+\eta)\)
とになります。
我々の興味の対象は、いつものように、\(\delta=0\)の場合と、\(\delta=\frac{pi}{2}\)の場合とですので、それぞれの場合について、2つの式がどのようになるかを見てみます。
まず、\(\delta=0\)の場合ですが、左側の式は
\(cos(\omega t)\cdot cos(0-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(0-\eta)\)
\(=cos(\omega t)\cdot cos(\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\eta)\)
となり、右側の式は
\(cos(\omega t)\cdot cos(0+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(0+\eta)\)
\(=cos(\omega t)\cdot cos(\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\eta)\)
となり、両者は一致することがわかります。
\(\delta=\frac{\pi}{2}\)の場合、\(sin(\frac{\pi}{2}\pm\theta)=cos(\theta)\)、\(cos(\frac{\pi}{2}\pm\theta)=\mp sin(\theta)\)、という三角関数の性質を利用すると、左側の式は
\(cos(\omega t)\cdot cos(\frac{\pi}{2}-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\frac{\pi}{2}-\eta)\)
\(=cos(\omega t)\cdot sin(\eta)-sin(\omega t)\cdot cos(\alpha)\cdot cos(\eta)\)
右側の式は、
\(cos(\omega t)\cdot cos(\frac{\pi}{2}+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\frac{\pi}{2}+\eta)\)
\(=-(cos(\omega t)\cdot sin(\eta) – sin(\omega t)\cdot cos(\alpha)\cdot cos(\eta))\)
となり、左側の式の符号を反転した値となります。
ここで元の式の分母を見ると、この項は2乗されますので、結果的に左の式と右の式とは同じ結果となることがわかります。
まとめると、MPギアのようにユニバーサルジョイントが左右対称に構成され、一定半径の曲線を走行する場合は、モーターの左右のユニバーサルジョイントの最終駆動面の角速度の変動は左右で同じになる、ということが今回の結論です。