気がつくとこのシリーズ20回目の記事です。よくもまぁここまで続けられるものだと我ながらあきれてしまいます。Shayの解析のあたりからは個人的興味で続けているところがありますので、万人にアピールする内容ではないと思いますが、よろしければ引き続きおつきあいください。今回からの考察では、別の概念を導入しますので少々難度が上がるかと思いますが、三角関数とベクトルの考え方がわかれば、理解できる内容になっているとは思います。

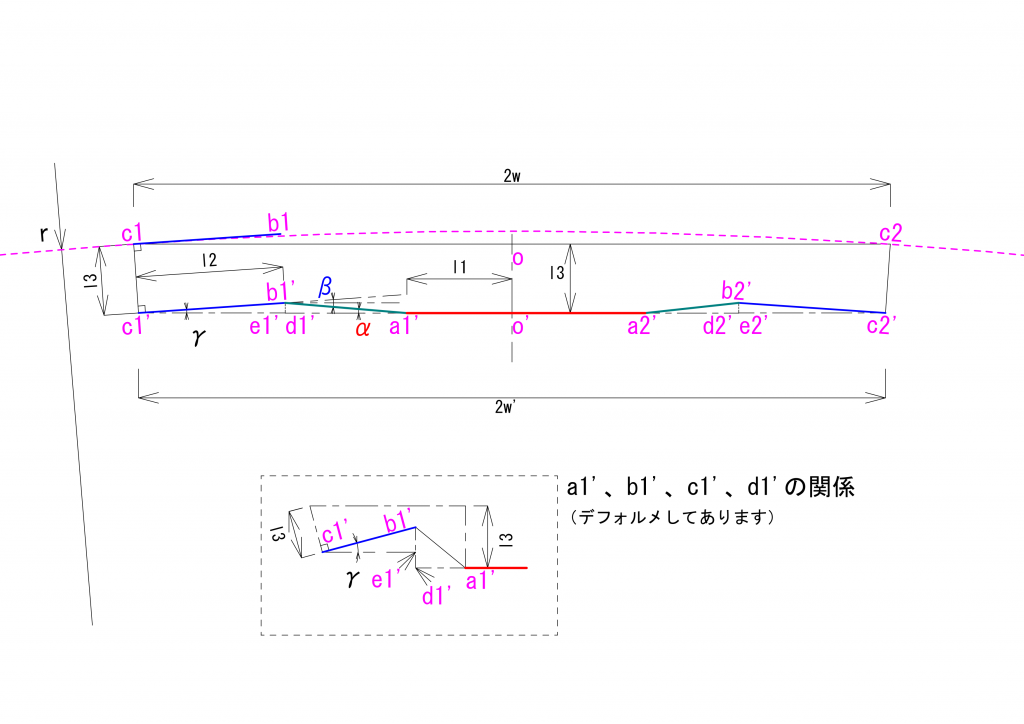
下の図は、２つのユニバーサルジョイントをつなげたときの解析で使ったものです。

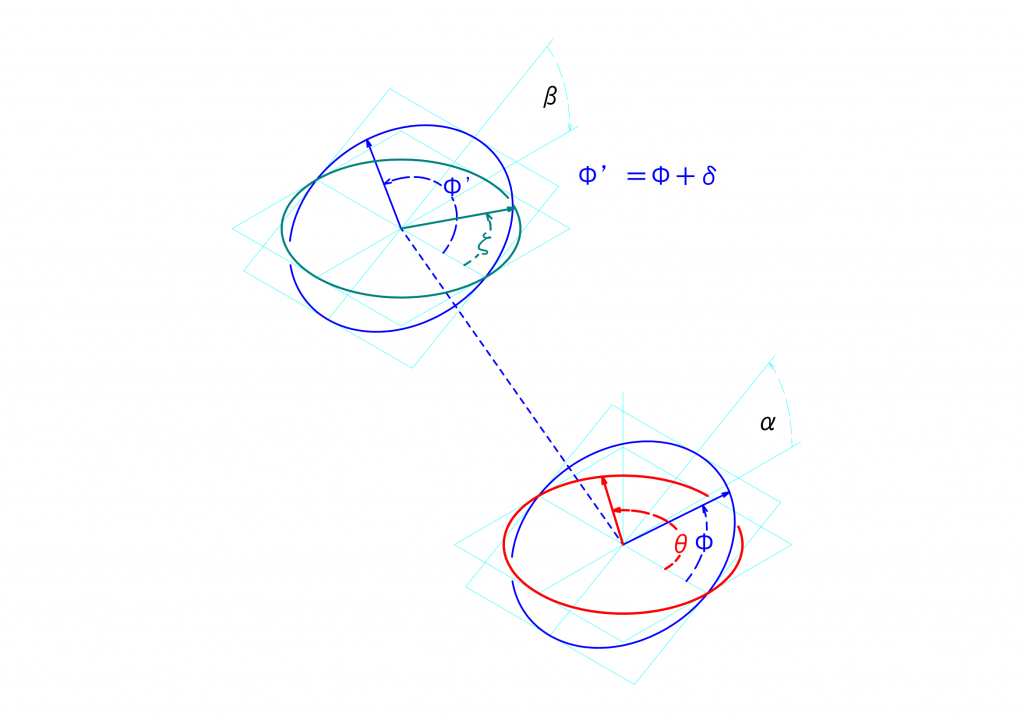
簡単におさらいしておくと、駆動面上の基準点がどれだけ回転したかの角度\(\theta\)と駆動面に対して\(\alpha\)傾いた伝達面上の基準点がどれだけ回転したかの角度\(\varphi\)に関して、

\(tan(\varphi) = -\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\alpha)}\)

が成立し、中継面上の基準点が回転した角度\(\varphi’\)と中継面に対して\(\beta\)傾いた最終伝達面上の基準点が回転した角度\(\xi\)に関して、

\(tan(\xi) = -\frac{1}{tan(\varphi’)}\cdot\frac{1}{cos(\beta)}\)

が成立します。

ここで、

\(\varphi’=\varphi + \delta\)

であり、\(\delta\)は伝達面に対する中継面の回転の位相のずれを表します。

ユニバーサルジョイントの角速度の変動を解析するには、\(\alpha\)、\(\beta\)を求め、\(\delta\)を定め、上記の関係から導出できる式にあてはめて計算してきました。

さて、ここまでの議論では一貫して一つの仮定を置いています。2つのユニバーサルジョイントを組み合わせたときに、ユニバーサルジョイントを構成する3つの軸がすべて同一平面上にある、というものです。

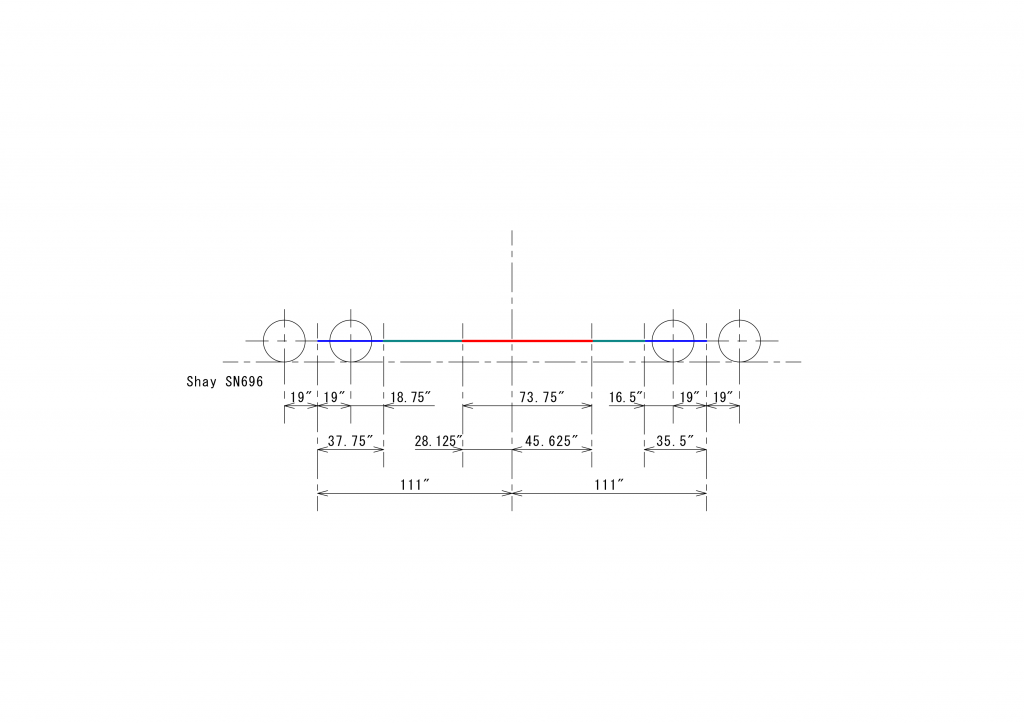
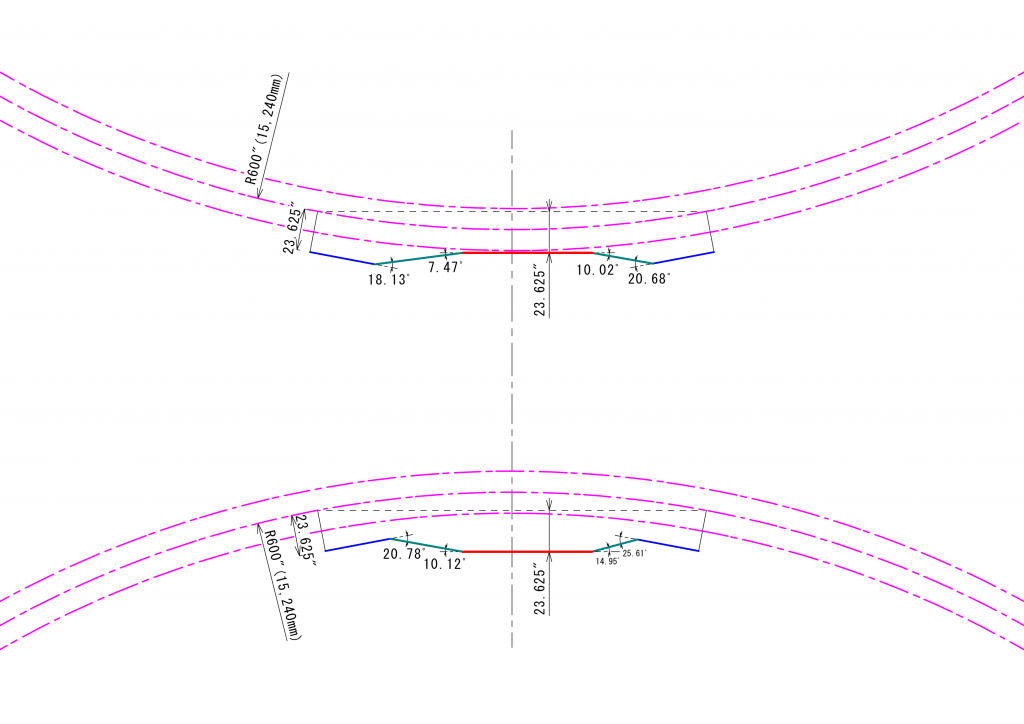
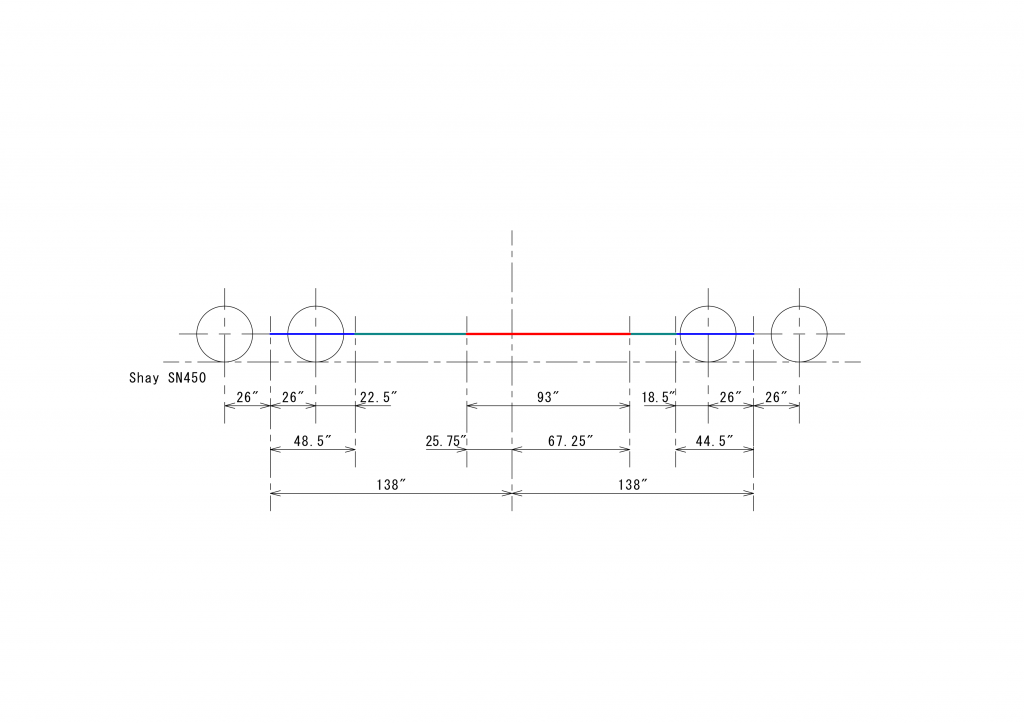
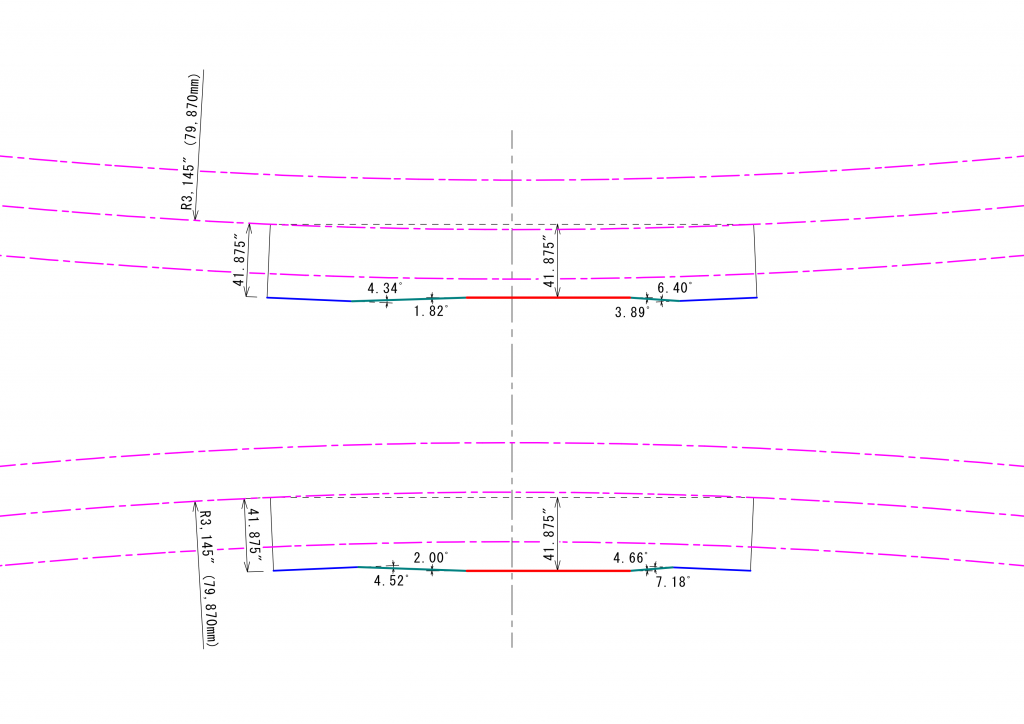
しかしながら、Shayの中には、エンジンのクランクシャフトの高さとベベルギアを駆動する台車の軸とが異なっているように見えるものがあります。写真の写し方によるのかとも思いましたが、このShayの図面を子細に確認すると、クランクシャフトの軸の高さはベベルギアを駆動する軸より1.5インチ高い位置にあるように読み取れます。

また、模型の中でも、モーターの軸の高さと、車輪を駆動する軸の高さがあっていないものを見たことがあります。

このような動力機構が曲線をを通過する場合、ユニバーサルジョイントを構成する３つの軸が同一平面上には存在するという仮定を満たしませんので、これまでの考え方では解析できません。以降、ユニバーサルジョイントを構成する３つの軸が同一平面上には存在しない場合の解析を考察します。

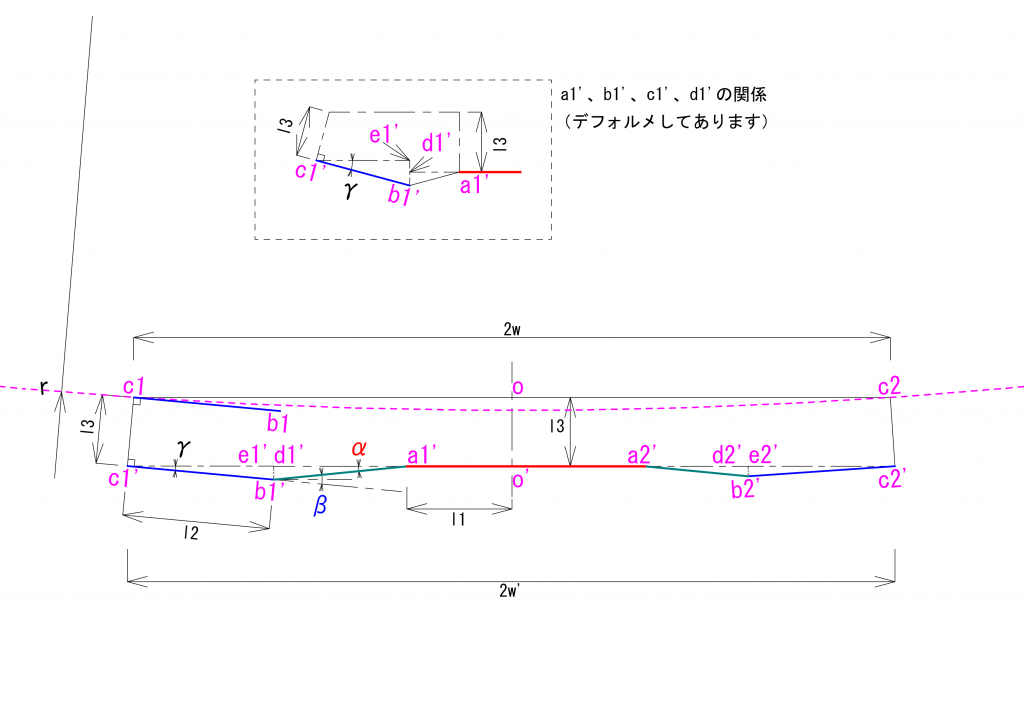
以下の説明をわかりやすくするために、先ほどの図と等価の図を図を座標系を明示して描いてみます。

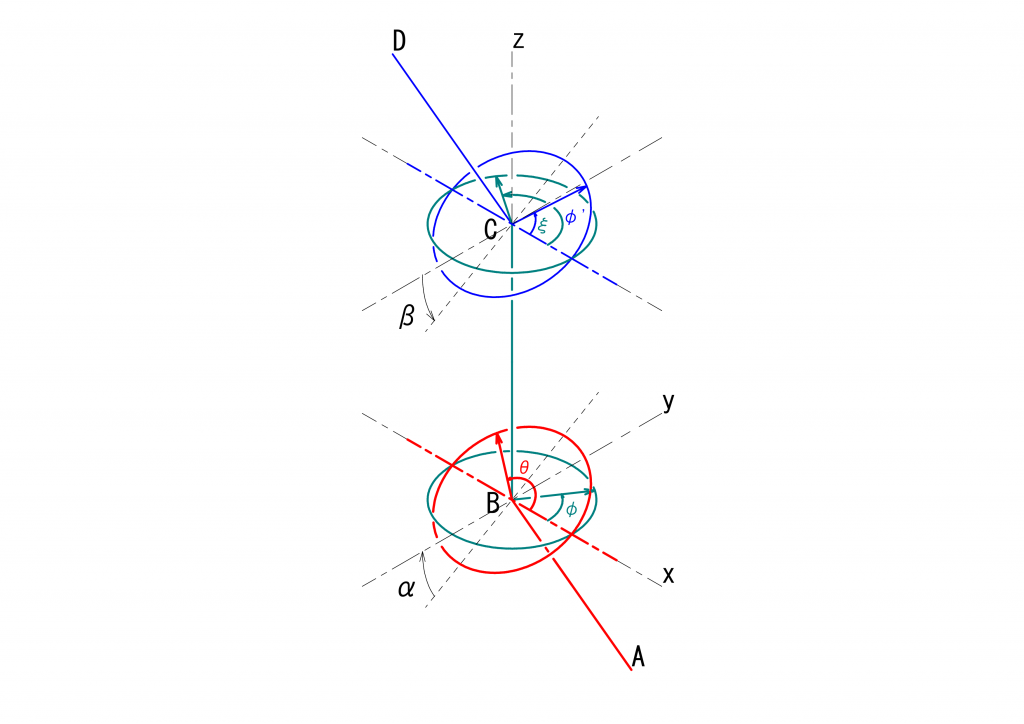
この図では、ユニバーサルジョイントを構成する３つの軸、\(AB\)、\(BC\)、\(CD\)、が\(y\)軸と\(z\)軸とからなる平面に配置されるように座標系を設定しています。同一平面上にあるということは、3つの軸を規定する４つの点\(A\)、\(B\)、\(C\)、\(D\)の\(x\)座標の値が\(0\)になるということです。ユニバーサルジョイントを構成する３つの軸が同一平面上にある場合、４つの点の\(x\)座標の値が\(0\)になるような座標系を設定することが可能である、という表現がより正確かもしれません。

解析に用いる\(\theta\)、\(\varphi\)、\(\varphi’\)、\(\xi\)を、どこを基準にして測るか、を考えてみます。\(\theta\)と\(\varphi\)を測る基準となるのは、駆動面と伝達面との2つの平面が交差する直線で、上図の赤の一点鎖線となります。同様に、\(\varphi’\)と\(\xi\)とを測る基準となるのは、中継面と最終伝達面との２つの平面が交差する直線で、上図の青の一点鎖線となります。3つの軸が同一平面上にある場合、これら２つの基準となる直線は平行となります。したがって、これらの4つの角度は、上記の図の例では\(x\)軸を基準に角度を測ればよい、ということになります。

３つの軸が同一平面にない場合の一例を示します。ここでは、先ほどの絵で\(A\)、\(B\)、\(C\)の位置は変わらず、\(CD\)が\(z\)軸周りに\(\eta\)回転したという様子を示しています。

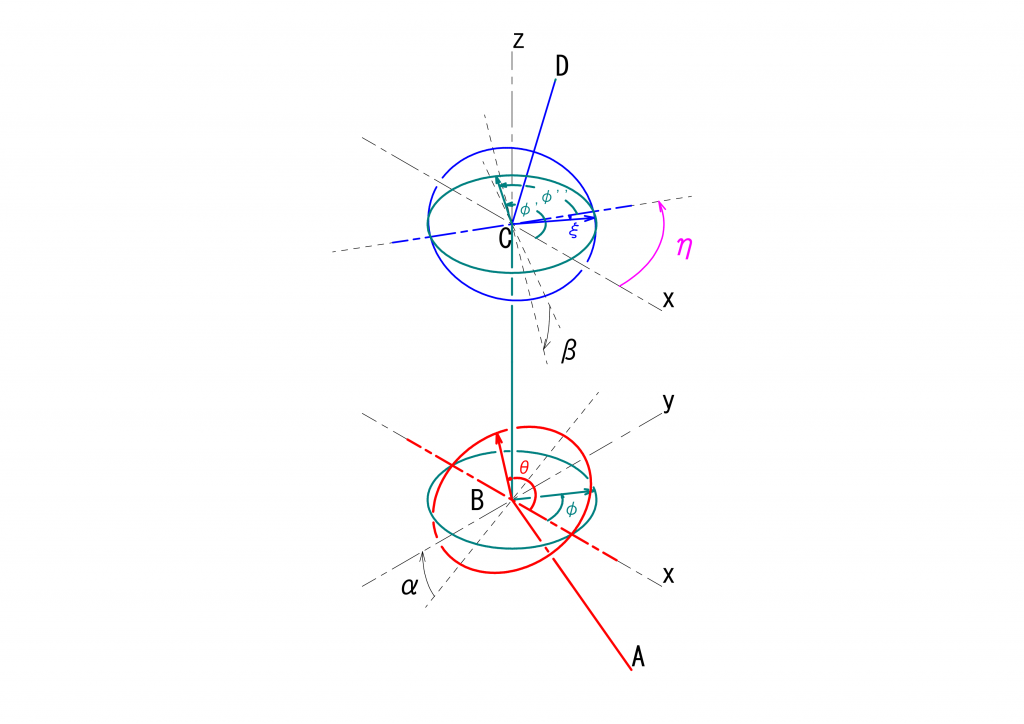
図を見ればわかる通り、駆動面と伝達面との2つの平面が交差する直線と、中継面と最終伝達面との２つの平面が交差する直線とは平行とはなりません。駆動面と伝達面との2つの平面が交差する赤い一点鎖線で示した直線に対する\(\theta\)と\(\varphi\)を測り、中継面と最終伝達面との２つの平面が交差する青い一点鎖線で示した直線に対する\(\varphi’’\)と\(\xi\)とを測り、これらの角度の間に成り立つ関係を求めなければなりません。

ここで、駆動面と伝達面との関係は前の場合と同じで、

\(tan(\varphi) = -\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\alpha)}\)

が成立します。

中継面と最終伝達面との関係は、

\(tan(\xi) = -\frac{1}{tan(\varphi’’)}\cdot\frac{1}{cos(\beta)}\)

が成立します。

\(CD\)が\(z\)軸を中心として\(\eta\)だけ回転したことを考慮する必要があり、

\(\varphi” = \varphi ’-\eta = \varphi + \delta – \eta\)

となります。\(\varphi’\)が\(\varphi\)に対してどれだけ位相がずれているかを\(\delta\)が表すのは今まで通りです。従って、これまで導出してきた角度や角速度の式の\(\delta\)を\(\delta-\eta\)で読み替えれば、そのまま利用することができます。

結論として、3つの軸が同一平面に存在しない場合にユニバーサルジョイントの角速度の変動を求めるには、\(\alpha\)、\(\beta\)、\(\eta\)を求めればよく、次回以降その具体的な求め方を考察してゆきます。

前回の記事の最後に、阿里山のShayがどの程度の角速度の変動があるのかを確認したいと述べていましたが、⼤変ありがたいことに、内⽥利次⽒、近藤⼀郎⽒より計算に必要な図面をご提供いただくことができました。御二⽅にはここに深く御礼申し上げます。ありがとうございました。

ということで、さっそく解析結果を掲載します。なお、最小半径は40mとしています。

---

まずは18tのShayの駆動系の寸法です。

最小半径での駆動軸の位置関係を示した図となります。

角速度がどのように変動するかのグラフです。これまでのように、駆動軸が円弧の内側に来る場合、外側に来る場合、の順で示します。

---

続いては28t Shayの駆動系の寸法です。

最小半径での駆動軸の位置関係を示します。

角速度の変動は以下のようになります。

---

これらのグラフから読み取れることを簡単にまとめてみたいと思います。

まず、位相が正しい場合、18t、28tとも、角速度の変動は±1%程度に抑えられますので、実用上は問題なさそうと言えそうです。また、前方の台車と後方の台車とで駆動系の寸法が大きくは変わらないことから、前後の角速度の変動の差があまり見られないのも特徴的です。

dda40xさんのBlogでは、阿里山のShayのユニバーサルジョイントは位相が正しくなさそうだとのことでしたので、角速度の変動が±2%程度発生していることになります。もっと条件の悪いShayもありましたので、それよりはスムーズに走るのかもしれませんが、それでも正しい位相にすれば、よりスムーズになる訳で、機械に対する負担も減ると思います。正しくない位相にするメリットは何もないと思います。

さて、前回の議論で、Shayの場合に\(\alpha\)と\(\beta\)との求め方を明らかにしましたので、MPギアの場合と同様に、駆動面に対する最終伝達面の角速度の変化を見てみたいと思います。

模型の寸法で議論ができればよいのでしょうが、MPギアのように標準的に使われているような部品がある訳ではないので、今回は実物の寸法を使うこととしました。Shayに関しては手持ちの資料があいにくと少なく、railtruckさんにご相談しデータを提供いただきました。この場を借りて深く御礼申し上げます。

まず、Serial Number 696のShayです。当初Gilpin Tramwayに導入され、その最小半径は50foot（約15m）であったとの記述があります。この条件で\(\alpha\)、\(\beta\)を求め、最終駆動面の角速度の変動をグラフ化してみます。

下図は、railtruckさんにいただいた図面から主要寸法を抜き出したものです。なお、寸法はすべてインチです（以後同様）。前回書いた通り、前の台車の駆動系の寸法と後ろの台車の駆動系の寸法とが異なりますので、それぞれについて\(\alpha\)、\(\beta\)を求める必要があります。

最小半径上で駆動軸がどう配置されるかを示したのが次の図です。CADで作図すると角度が正確にでるのはありがたいですね。導出した式で計算した値と一致することを確認しています。

早速グラフにしてみます。まずは駆動軸が円弧の内側にある場合の角速度の変動。

続いて、駆動軸が円弧の外側にある場合の角速度の変動。

この２つのグラフから言えることをいくつか挙げてみたいと思います。

まず駆動軸が円弧の外側にある場合の方が角速度の変動率が小さいということで、これは我々の直感に沿っているかと思います。

ユニバーサルジョイントの位相が揃っている場合でも、角速度の変動が±5%程度ありますが、極めて小さな回転半径に起因するものです。MPギアでは、5%に近づくあたりを境に走行のスムーズさに影響を与えるという仮説を立てましたので、この機関車も最小半径のところでは影響があったのでしょうか。

位相が揃っていなければ、駆動軸が内側にある場合、±15%近く変動しますので、もし間違えてこの構成にしていたとしたら、低速でも相当の振動になったのではないかと推測します。

後ろの台車の駆動系より、前の台車の駆動系の\(l_1\)の長さが長いことで、前の台車の角速度の変動の方が大きいのは、MPギアの時に考察した通りです。

---

次はSerial Number 450のShayです。こちらもrailtruckさんにいただいた図面から主要寸法を抜き出しました。このShayの特徴は、前の台車の駆動軸の寸法と、後ろの台車の駆動軸の寸法とが著しく異なることです。当然、前の台車と後ろの台車とで、角速度の変動が大きく異なることが想像されます。

これは標準軌のShayなのですが、活躍していた鉄道の曲線の最小半径に関する情報が見つかりませんでした。後述するWestern MarylandのShayが22度のカーブを走れるようにしていたという記述がありましたので、仮にこの数値を採用することとしました。こちらの情報によれば、22度のカーブというのは、半径262.042フィート(約80メートル)ということです。Western MarylandのShayに比べるとだいぶん小ぶりの機関車ですので、もっと最小半径は小さかったと想像します。もしも詳細な情報が入手できれば、後日追記します。

角速度の変動をグラフにしてみました。

いずれの場合も、角速度の変動率は1%以内には収まっていますが、これは上述したように最小半径が大きいことと、前後の寸法が違うとはいえ、ホイールベースが大きめにとってあることによると思います。

グラフでは示しませんが、最小半径を半分にしたとしても、ユニバーサルのジョイントの位相が揃っている限り角速度の変動率は2%に収まっていますので、これも大きめのホイールベースが寄与していると考えます。

ただし、前方の台車と後方の台車との駆動軸の寸法が大きく異なっていることから、前方の台車の角速度の変動は後方の台車の角速度の変動の差は大きいことがわかります。

---

最後は、Western MarylandのShayです。こちらは、先日書棚を整理しているときに、Train Shed Cyclopedia No.49の中に偶然見つけたものです。1945年Lima社製で、最後に製造したShayであり、かつ最大のShayです。主要寸法は下図のとおりで、これまでの2台に比べると圧倒的に大きな機関車です。前回述べたように、3つ目の台車については今回の検討対象とはしません。

上述のとおり、このShayは22度のカーブを走行できるようにしたとの記述がTrain Shed Cyclopediaの中にあります。最小半径で走行時の駆動系がどのような位置関係にあるか、を下に示します。

グラフです。

先ほどのSN 450のShayに比べても、ホイールベースはさらに大きく、駆動系の寸法にも余裕があるため、ユニバーサルジョイントの位相が揃っている場合は角速度の変動率が±1%に収まっています。実用上はほとんど問題のないレベルではなかったかと推測します。

---

以上、3つのShayの場合の角速度の変動を計算してみました。本当は阿里山のShayがどうやら位相が揃っていないとのことですので、どの程度の角速度の変動があるのかを確認したいのですが、正確な寸法が入手できないので、今回はここまでとします。

このシリーズを延々続けているのは、Shayのユニバーサルジョイントの角速度の変化を解析したかったからでした。ということで、Shayの場合の\(\alpha\)と\(\beta\)とを求めてみます。

求め方はMPギアの場合に準じますが、MPギアの駆動軸が車体の中心に位置するのに対し、Shayの駆動軸は車体の中心からオフセットしていることを考慮に入れる必要があります。更に、駆動軸が曲線の内側に存在する場合と、曲線の外側に存在する場合との場合わけが必要となります。

私の入手したShayの図面で確認した範囲では、エンジンから前方の台車に動力を伝える駆動軸の寸法と、エンジンから後方の台車に動力を伝える駆動軸の寸法とは異なります。ただし、これはそれぞれについて\(\alpha\)と\(\beta\)とを求めればよいと言う事ですので、計算の方法には影響がありません。下記の議論では片方のみを取り上げます。

もう一つお断りしておくと、3(4)トラックShayになると更に2(4)つのユニバーサルジョイントを介して、後方の台車に動力が伝えられます。ここまで議論してきた事を応用すれば解析は可能ですが、今回の議論の対象外とします。

下に示したのは、半径\(r\)の円弧上をShayが走行しており、駆動軸が円弧の内側（円弧の中心に近い側）にあるときの図です。

MPギアの場合と同様、\(c_1\)と\(c_2\)とが台車の中心を、\(o\)が\(c_1\)、\(c_2\)との中心点を示します。また、線分\(c_1c_2\)の長さを\(2w\)とします。MPギアの場合と同様、台車の線路方向の中心軸は、円弧上の\(c_1\)と\(c_2\)とで接すると言う仮定をおきます。\(c_1\)に接する線分\(c_1b_1\)は、\(c_1\)と円弧の中心\(O_r\)（注：図には示していません）とを結んだ線と直交するということです。

Shayの駆動軸が車体中心に対してどれだけオフセットしているかの寸法を\(l_3\)とします。

\(o’\)は駆動軸の中心位置を、\({a_1}’\)、\({a_2}’\)はエンジン側のユニバーサルジョイントの位置を、\({b_1}’\)、\({b_2}’\)は台車側のユニバーサルジョイントの位置を示します。\({c_1}’\)、\({c_2}’\)は、それぞれ\(c_1\)、\(c_2\)から、円弧の中心\(O_r\)に向かって長さ\(l_3\)の線分を引いた位置を示します。

MPギアと異なり、\(o’\)、\({a_1}’\)、\({a_2}’\)を結ぶ直線状に\({c_1}’\)、\({c_2}’\)は存在しません。\({a_1}’\)、\({a_2}’\)から垂線を下した時に、\({a_1}’\)、\({a_2}’\)を通る直線と交差する点をそれぞれ\({d_1}’\)、\({d_2}’\)と、\({c_1}’\)、\({c_2}’\)を通る直線と交差する点をそれぞれ\({e_1}’\)、\({e_2}’\)とします。

線分\(o'{a_1}’\)の長さを\(l_1\)、線分\({b_1}'{c_1}’\)の長さを\(l_2\)、線分\({c_1}'{c_2}’\)の長さを\(2w’\)とします。線分\({c_1}'{e_1}’\)と線分\({c_1}'{b_1}’\)とのなす角を\(\gamma\)、線分\({a_1}'{b_1}’\)と線分\({a_1}'{d_1}’\)とのなす角度を\(\alpha\)、線分\({b_1}'{a_1}’\)と線分\({c_1}'{b_1}’\)を車体の中心方向に延長した線とのなす角を\(\beta\)とします。

このような前提で\(\alpha\)、\(\beta\)を求めます。まず、円弧の中心\(O_r\)と\({c_1}\)と\(o\)とがなす三角形と、円弧の中心\(O_r\)と\({c_1}’\)と、\({c_1}'{e1}’\)を車体の中心方向に延長した線と\(O_r\)、\(o\)を通る直線との交点とがなす三角形とは相似ですので、MPギアの場合と同様、

\(cos(\gamma)=\frac{w}{r}\)

が成り立ちます。

また、上記２つの三角形が相似であるということは、\(w:r =w:'(r-l_3)\)が成立するということですので、

\(w’=w\cdot\frac{r-l_3}{r}\)

が成り立ちます。

次は\(\alpha\)を求めます。

まず、線分\({a_1}'{d_1}’\)の長さは、\(w’-l_1-l_2\cdot cos(\gamma)\)となります。

線分\({b_1}'{d_1}’\)の長さは、線分\({b_1}'{e_1}’\)の長さ\(l_2\cdot sin(\gamma)\)と、線分\({e_1}'{d_1}’\)の長さ\(l_3 – l_3\cdot cos(\gamma)\)との和、\(l_2\cdot sin(\gamma)+l_3 – l_3\cdot cos(\gamma)\)となります。

\({a_1}’\)、\({b_1}’\)、\({e_1}’\)のなす直角三角形に注目すると、

\(tan(\alpha)=\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w’-l_1-l_2\cdot cos(\gamma)}\)

\(=\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w\cdot\frac{r-l_3}{r}-l_1-l_2\cdot cos(\gamma)}\)

が成り立ちます。

従って、半径\(r\)の円を走行中のShayのユニバーサルジョイントの\(\alpha\)と\(\beta\)とは、

\(\gamma=cos^{-1}(\frac{w}{r})\)

\(\alpha=tan^{-1}(\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w\cdot\frac{r-l_3}{r}-l_1-l_2\cdot cos(\gamma)})\)

\(\beta=\alpha+\gamma\)

と求める事ができます。

次は、下図のように駆動軸が円弧の外側に来た場合の式を考えてみます。

座標や長さの考え方は、駆動軸が円弧の内側に来た場合と同じですので省略し、\(\alpha\)、\(\beta\)、\(\gamma\)をさっそく求めてみます。

円弧の中心\(O_r\)と\({c_1}\)と\(o\)とがなす三角形と、円弧の中心\(O_r\)と\({c_1}’\)と、\({c_1}'{e1}’\)を車体の中心方向に延長した線と\(O_r\)、\(o\)とを通る直線との交点と、がなす三角形とは相似ですので、

\(cos(\gamma)=\frac{w}{r}\)

が成り立ちます。また、上記２つの三角形の相似であるということは、\(w:r =w’:(r+l_3)\)が成立するということですので、

\(w’=w\cdot\frac{r+l_3}{r}\)

が成り立ちます。

線分\({a_1}'{d_1}’\)の長さは\(w’-l_1-l_2\cdot cos(\gamma)\)となります。線分\({b_1}'{d_1}’\)の長さは、線分\({b_1}'{e_1}’\)の長さ\(l_2\cdot sin(\gamma)\)から線分\({e_1}'{d_1}’\)の長さ\(l_3 – l_3\cdot cos(\gamma)\)を引いた、\(l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)\)となりますので、

\(tan(\alpha)=\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w’-l_1-l_2\cdot cos(\gamma)}\)

\(=\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w\cdot\frac{r+l_3}{r}-l_1-l_2\cdot cos(\gamma)}\)

が成立します。これらの式から、

\(\gamma=cos^{-1}(\frac{w}{r})\)

\(\alpha=tan^{-1}(\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w\cdot\frac{r+l_3}{r}-l_1-l_2\cdot cos(\gamma)})\)

\(\beta=\alpha+\gamma\)

と導き出すことができます。

次回はこれらの式に具体的な数値を当てはめてみたいと思います。