次に、２つのユニバーサルジョイントを組み合わせる事を考えます。

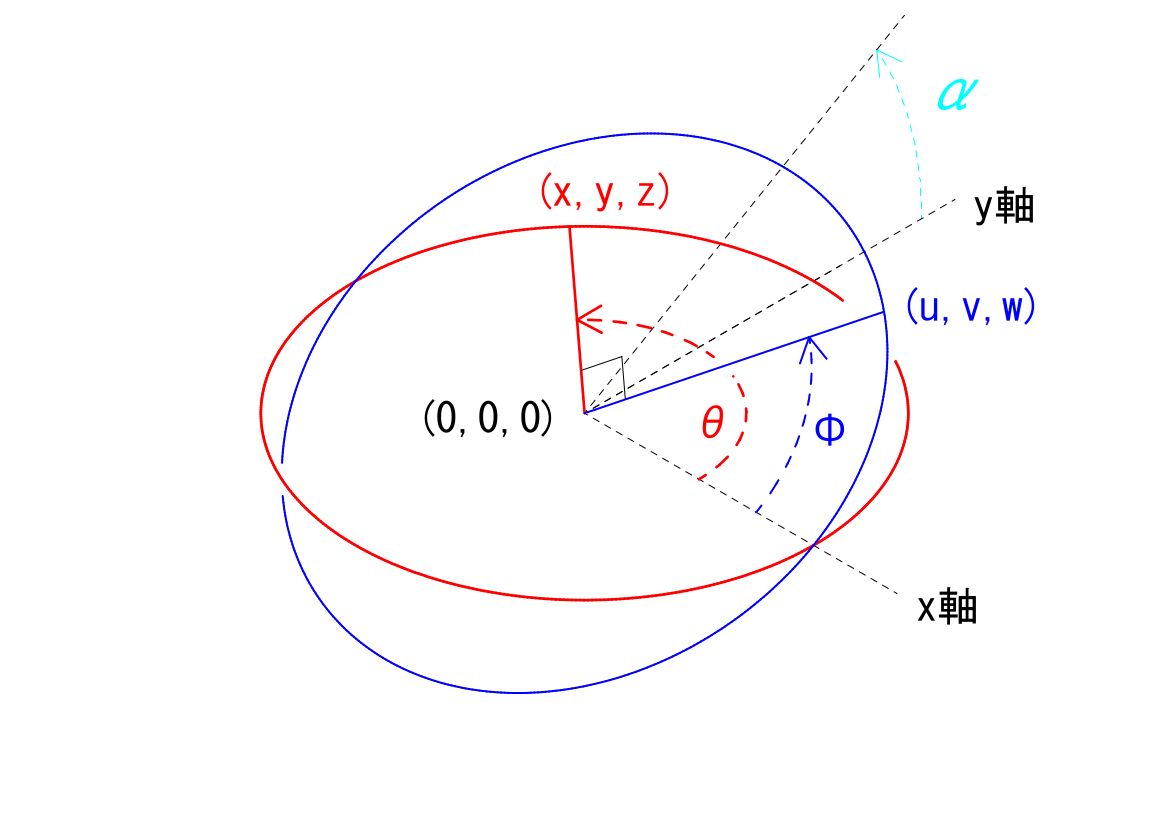
まず、前回の議論で、駆動面に対し伝達面が\(\alpha\)だけ傾いている場合、駆動面を回転する基準点の\(x\)軸に対する角度\({\theta}\)と、伝達面を回転する基準点の\(x\)軸に対する角度\({\varphi}\)とには、次の関係が成立することを示しました。

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\alpha)}\)

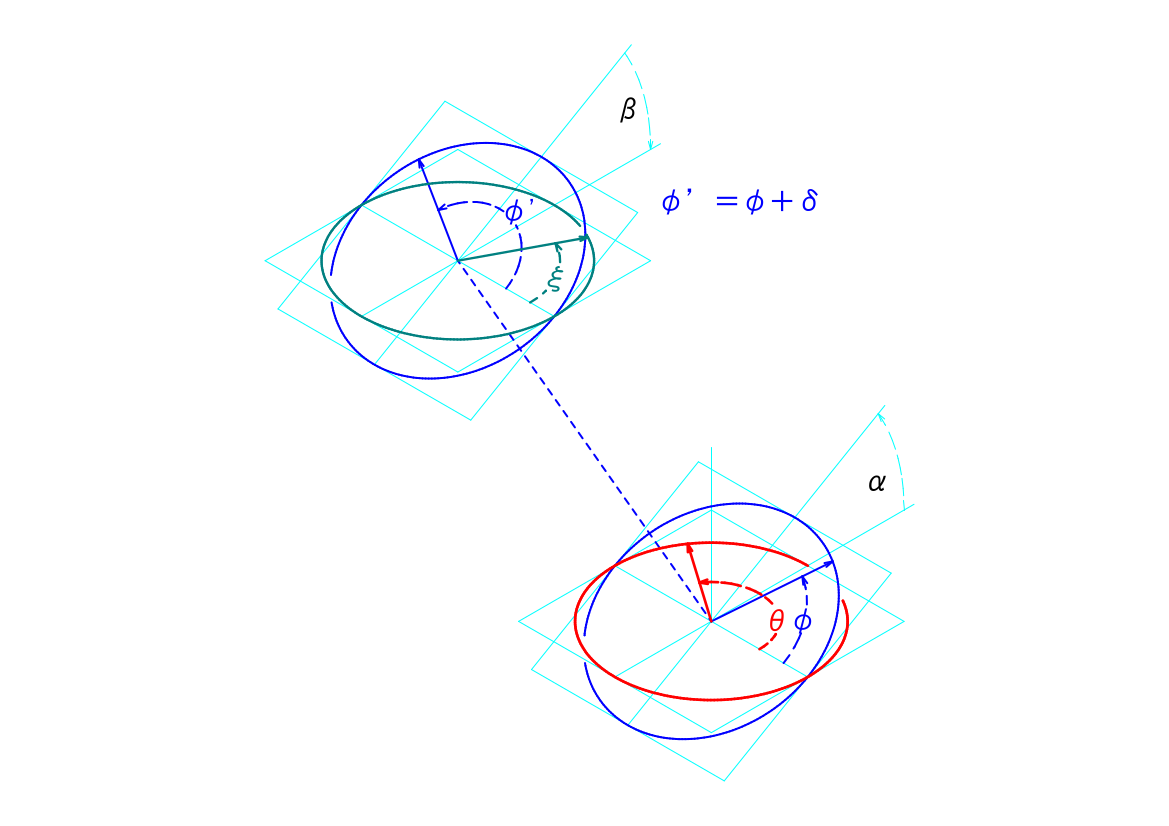
この伝達面の先に、もう一つのジョイントをつなげることを考えます。下図にこの様子を示します。

図の下にある赤の円が駆動面で、青の円が伝達面を示します。それぞれの基準点の角度が\(\theta\)、\(\varphi\)となります。

もう一つのジョイントの十字型部品の基準点の移動する円を２つ、図の上の方に青の円と緑の円とで示します。ここでは、青の円を中継面、緑の円を最終伝達面、と呼ぶこととします。なお、議論を簡単にするために、ここでは駆動面につながっている軸、伝達面と中継面をつなぐ軸、最終伝達面につながっている軸、の３つは、同一平面上にあるものとします。

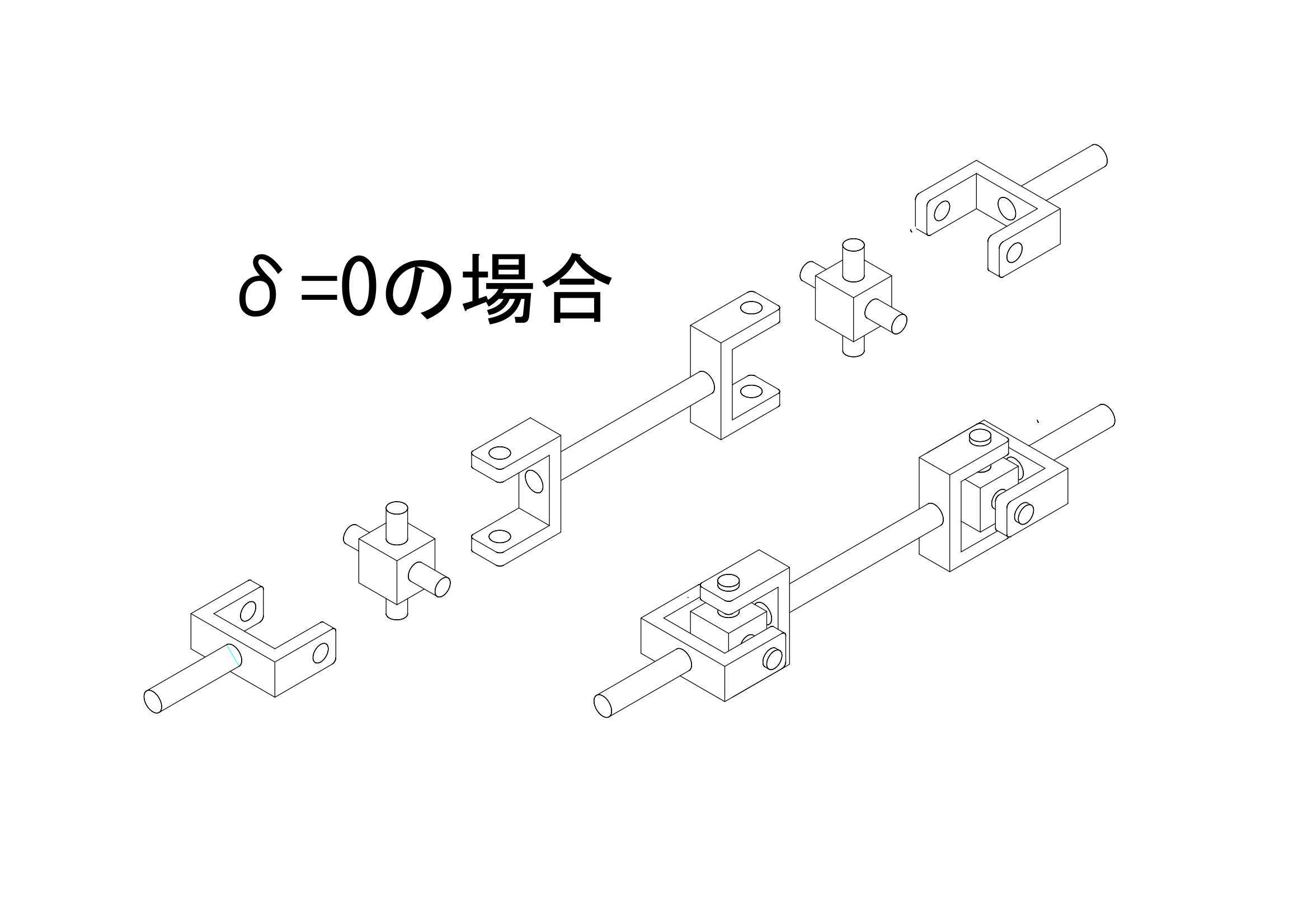
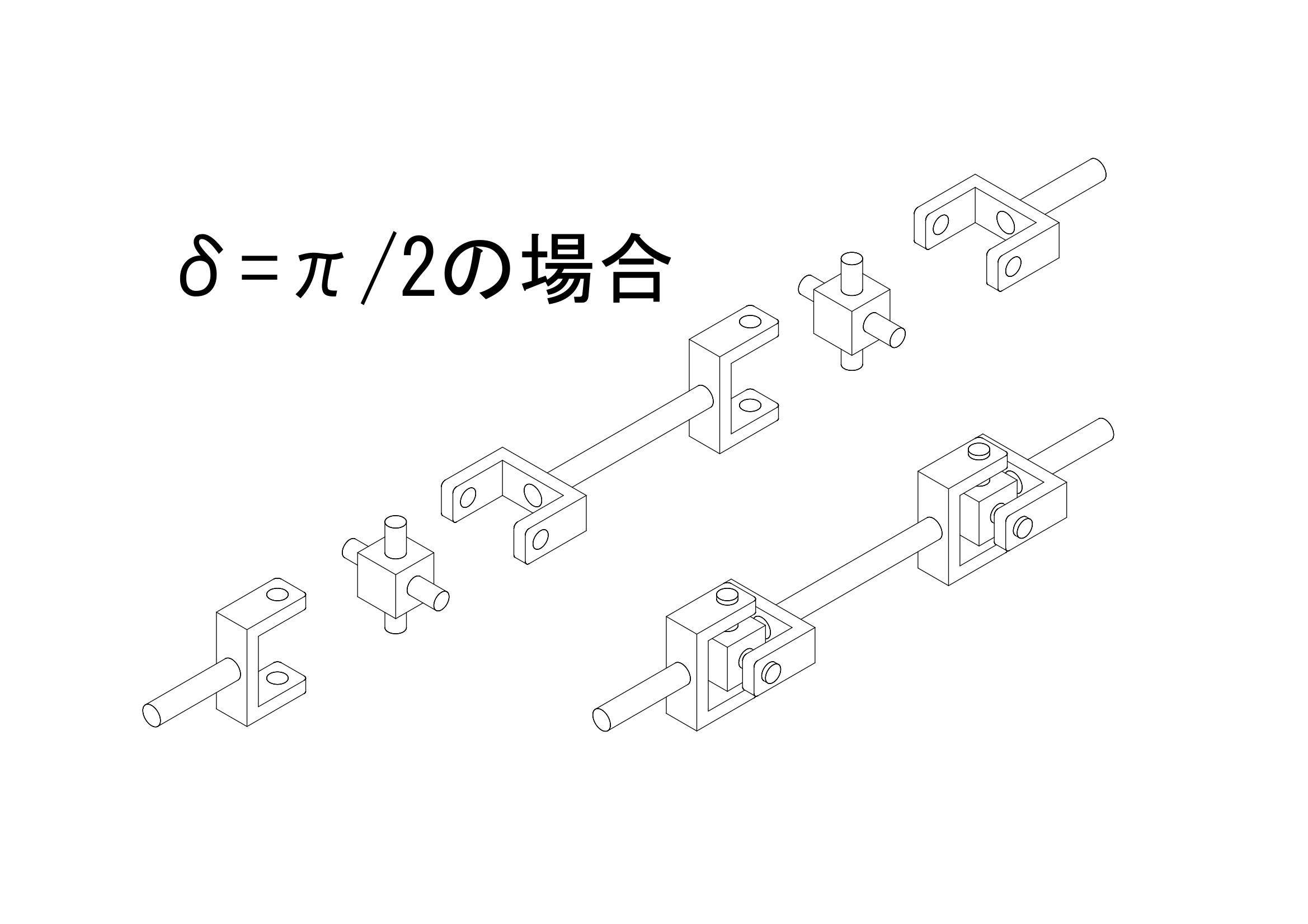
中継面は伝達面と平行であり、その中継面上を移動する基準点の角度を\(\varphi\prime\)とし、伝達面の基準点の角度\(\varphi\)に対して、\(\varphi\prime=\varphi+\delta\)という関係が成り立つものとします。つまり\(\delta=0\)であれば、ジョイントは同位相で、\(\delta=\frac{\pi}{2}\)であれば、ジョイントは90度ひねられて取り付けられていることとなります。

また、最終伝達面は、中継面に対して\(\beta\)傾いているものとし、最終伝達面の基準点の角度を\(\xi\)とします。

さて、中継面の基準点の角度\(\varphi\prime\)と最終伝達面の基準点の角\(\xi\)との関係は、\(\theta\)と\(\varphi\)との関係と同じで、次の式が成り立ちます。

\(tan(\xi)=-\frac{1}{tan(\varphi^\prime)}\cdot\frac{1}{cos(\beta)}\)

\(\varphi^\prime=\varphi+\delta\)でしたので、上記の式は、

\(tan(\xi)=-\frac{1}{tan(\varphi+\delta)}\cdot\frac{1}{cos(\beta)}\)

となります。

上記の式の中の\(tan(\varphi+\delta)\)に注目します。2つの角度の和のタンジェントは次のように書き変えることができます。

\(tan(\varphi+\delta)=\frac{tan(\varphi)+tan(\delta)}{1-tan(\varphi)\cdot tan(\delta)}\)

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\)を代入すると、

\(tan(\varphi+\delta)\) = \(\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+tan(\delta)}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot tan(\delta)}\)

となり、\(tan(\delta)=\frac{sin(\delta)}{cos(\delta)}\)であったことを思い出し、分子と分母とに\(tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)\)をかけると、

\(tan(\varphi+\delta)=\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+\frac{sin(\delta)}{cos(\delta)}}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot \frac{sin(\delta)}{cos(\delta)}}=\frac{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}\)

これを、最初の式に代入すると

\(tan(\xi)=-\frac{1}{tan(\theta+\delta)}\cdot \frac{1}{cos(\beta)}=-\frac{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

となり、少し見やすく整理すると、

\(tan(\xi)=\frac{sin(\delta)+tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta)-tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

という式が得られます。

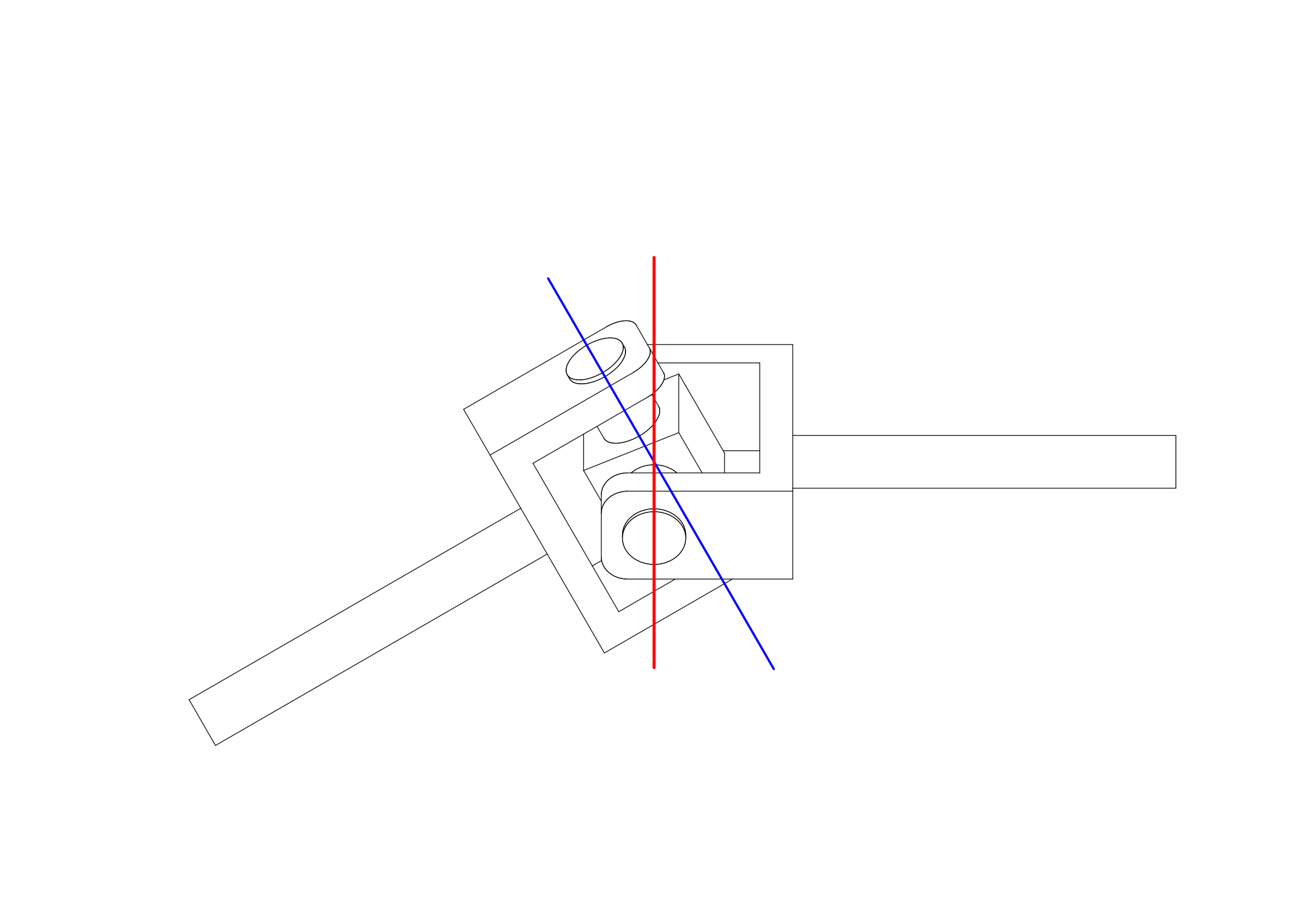
さて、いつも議論となるのは、ジョイントが同位相か、\(\frac{\pi}{2}\)（90度）ひれらているかです。

上の図のように、ジョイントを同位相とするということは、\(\delta=0\)とするということですので、\(sin(0)=0\)、\(cos(0)=1\)となります。これを代入すると

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}\)

となります。従って、\(\alpha=\beta\)であれば、

\(tan(\xi)=tan(\theta)\)

となります。

この式は、ジョイントを同位相にし、2つのジョイントの傾きを同じにしておけば、一方のジョイントの不等速性は、もう一方のジョイントで打ち消され、駆動面と、最終伝達面との位相とは、同じであり、等速性が保証される、ということとなります。

また、\(cos(\theta)=cos(-\theta)\)であったことを思い出すと、上記の式は、

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(\alpha)}{cos(-\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(-\beta)}\)

のいずれでも成立することがわかります。つまり、上で述べたジョイントの2つの傾きが同じ、というのは、傾きの絶対値が同じと言い換えてよいことがわかります。

上の図のように、ジョイントを90度回転させると、\(\delta=\frac{\pi}{2}\)となりますので、\(sin(\frac{\pi}{2})=1\)、\(cos(\frac{\pi}{2})=0\)を先ほどの式に代入すると、

\(tan(\xi)=-\frac{1}{tan(\theta)\cdot cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、少し変形すると、

\(tan(\xi)=tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、ユニバーサルジョイント1個の時によく似た形の式となります。異なるのは、\(\frac{1}{cos(\beta)}\)が付け加わっていることです。

ユニバーサルジョイント1個の時は、駆動面の基準点の角度に比して、伝達面面の基準点の角度が進む、ということでしたが、ユニバーサルジョイント2個の際は、さらにもう一回角度が進むこととなり、つまりは、不等速性を増大させる、ということがわかります。

（この項続く）

 

数学でベクトルという概念があり、その基本的な性質の一つが、「直交する2つのベクトルの内積は0になる」というものです。わかりやすく言うと、原点\((0,0)\)から、座標\((x,y)\)を結んだ線と、原点\((0,0)\)から、座標\((u,v)\)を結んだ線とが直交する、つまり90度で交わる場合、\(x \cdot u + y \cdot v\)は必ずゼロになるということです。

直交するベクトルの内積が0になるというのは、3次元空間でも成り立ち、３次元の座標\((x,y,z)\)と\((u,v,w)\)とがあったときに、原点\((0,0,0)\)とこれらを結ぶ２つの線が直交する場合は、\( x \cdot u + y \cdot v + z \cdot w =0\)が成立します。

ユニバーサルジョイントの十字型の部品の２つの軸は直交していますので、２つの基準点の座標についても、上記の性質が成り立ちます。

\((x,y,z)=(r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

\((u,v,w) = (r\cdot cos(\varphi), r\cdot sin(\varphi)\cdot cos(\alpha), r\cdot sin(\varphi)\cdot  sin(\alpha))\)

でしたので、

\(r \cdot cos(\theta) \cdot r \cdot cos(\varphi) + r \cdot sin(\theta) \cdot r \cdot sin(\varphi) \cdot cos(\alpha) + 0\cdot r \cdot sin(\varphi)\cdot sin(\alpha) = 0\)

となります。式を整理すると、

\(r ^2 \cdot sin(\theta) \cdot sin(\varphi) \cdot cos(\alpha) = – r ^2 \cdot cos(\theta) \cdot cos(\varphi)\)

となり、両辺を\(r^2 \cdot cos(\varphi) \cdot sin(\theta)\cdot cos(\alpha) \)で割ると、

\(\frac{sin(\varphi)}{cos(\varphi)} = – \frac{cos(\theta)}{sin(\theta) \cdot cos(\alpha)}=-\frac{1}{\frac{sin(\theta)}{cos(\theta)}}\cdot\frac{1}{cos(\alpha)}\)

\( \frac{sin(\theta)}{cos(\theta)}=tan(\theta) \) でしたから、この式は

\(tan(\varphi) = – \frac{1}{tan(\theta)} \cdot \frac{1}{cos(\alpha)}\)

となります。\(tan\)の周期性の性質を利用してもう少し変形すると、

\(tan(\varphi) = tan(\theta-\frac{\pi}{2})\cdot \frac{1}{cos(\alpha)}\)

という式が得られます。\(\theta =\frac{\pi}{2}\)の時、\(\varphi=0\)となるのでした。従って、この式が基準点の位置関係を的確に表現しています。

説明がこなれていないですが、この式からわかることを書いてみたいと思います。

\(\alpha > 0 \)を想定していますので、\(cos(\alpha) < 1\)となります。従って、\(tan(\varphi)\)は、\(tan(\theta-\frac{\pi}{2})\)より大きな値になります。このことは、\(\varphi\)は、\(\theta-\frac{\pi}{2}\)よりも角度が大きい、つまり、伝達面の基準点の回転角は、駆動面の基準点の基準点の回転角よりも進んでいる、ということを示しています。

\(\frac{1}{cos(\alpha)}\)の影響を受けない場合があり、それは両辺の\(tan\)が\(0\)か\(\infty\)となる場合で、その組み合わせは

\(\theta=\frac{\pi}{2}, \varphi=0\)

\(\theta=\pi, \varphi=\frac{\pi}{2}\)

\(\theta=-\frac{\pi}{2}, \varphi=\pi\)

\(\theta=0, \varphi=-\frac{\pi}{2}\)

の４つです。これらが成立するのは、基準点のいずれかが、\(x\)軸上にあるときで、\(\frac{\pi}{2}\)つまり、90度ごとに駆動面と伝達面との基準点の回転角が一致するものの、それ以外は、伝達面の基準点の回転角の方が大きくなるということで、このために不等速性が発生するということが言えると思います。

さて、上記の式を\(\varphi\)について解くと、

\(\varphi = tan^{-1}(\frac{tan(\theta-\frac{\pi}{2})}{cos(\alpha)})\)

となります。この計算式を使えば、駆動面の基準点の角度が与えられたときに、伝達面の基準点の角度を計算することができます。

 

ユニバーサルジョイントを構成する十字型の部品の2つの軸の先端がどこを動くか、を示したのが次の図となります。ここで、十字型の部品の中心、つまり、２つの軸が交差する点を原点\((0,0,0)\)とします。また、水平面上（赤い円）を移動する軸に取り付けられたフォーク状の部品に動力が供給され、それが傾いた面上（青い円）を移動する軸に伝達されるとします。ここでは仮に、水平な面を「駆動面」と、傾いた面を「伝達面」と呼ぶこととします。

原点と十字の二軸のそれぞれの一方の先端だけに注目したのが、次図です。以下、この注目した軸の先端を「基準点」と呼ぶこととします。基準点の選び方によって、多少式が変わってきますが、最終的には同等の結果が得られます。

駆動面を動く基準点は、原点\((0,0,0)\)を中心に、水平面上の半径\(r\)の円を回転し（上図の赤い円）、伝達面を動く基準点は、原点を中心に、駆動面に対して角度\(\alpha\)傾いた面の上の半径\(r\)の円を回転します（同じく青い円）。

このとき、駆動面の基準点の座標を\((x,y,z)\)、伝達面の基準点の座標を\((u,v,w)\)であるとします。更に、\((x,y,z)\)の駆動面における\(x\)軸に対する角度を\(\theta\)とし、\((u,v,w)\)の伝達面における\(x\)軸に対する角度を\(\varphi\)とします。

駆動面の基準点の座標は、三角関数の定義から、

\((x,y,z)=(r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

となります。

伝達面の基準点の座標を求めると、まず\(x\)座標の値\(u\)は、被駆動面の傾きによらず、

\(u = r\cdot cos(\varphi)\)

となります。

座標\((u,v,w)\)と座標\((u,0,0)\)の距離は、\(r\cdot sin(\varphi)\)となります。座標\((u,0,0)\)、\((u,v,0)\)、\((u,v,w)\)からなる直角三角形を考えると、この底辺の長さ、高さがそれぞれ\(u\)、\(v\)となり、伝達面の傾きが\(\alpha\)なので、

\(v = r\cdot sin(\varphi)\cdot cos(\alpha)\)

\(w = r\cdot sin(\varphi)\cdot sin(\alpha)\)

となります。まとめると、

\((u,v,w) = (r\cdot cos(\varphi), r\cdot sin(\varphi)\cdot cos(\alpha), r\cdot sin(\varphi)\cdot  sin(\alpha))\)

となります。

 

念のため、今回の議論に必要となる最低限の三角関数の復習をしておきます。

原点\((0,0)\)から長さ\(r\)の線分が傾き\(\theta\)でひかれているとします。

このとき、線分の先端の座標は\((r\cdot sin(\theta),r\cdot cos(\theta))\)となります。

また、\(sin(\theta)\)を\(cos(\theta)\)で割った値を\(tan(\theta)\)と呼びます。つまり、

\(tan(\theta)=\frac{sin(\theta)}{cos(\theta)}\)

です。

角度の表現は、一般に使われる度ではなく、ラジアン表現を使います。ここでは、\(\pi=180^{\circ}\)、\(\frac{\pi}{2}=90^{\circ}\)ということだけ思い出していただければ結構です。

いくつか代表的な値をあげておくと、

\(sin(0)=0\)

\(cos(0)=1\)

\(sin(\frac{\pi}{2})=1\)

\(cos(\frac{\pi}{2})=0\)

となります。

このほか、以下の式が成立します。

\(tan(\theta-\frac{\pi}{2})=tan(\theta+\frac{\pi}{2})=-\frac{1}{tan(\theta)}\)

\(cos(\theta)=cos(-\theta)\)

また、2つの角度の和のタンジェントはそれぞれの角度のタンジェントを用いて、次のように表現できます。

\(tan(\alpha+\beta)=\frac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)\cdot tan(\beta)}\)

今回の議論で必要な三角関数に関する知識は、以上です。

本格的に三角関数を復習されたい方は、以下のビデオがわかりやすいかと思います。

２つの軸が斜めに接続されて回転するということは、そもそもどういうことかということを考えてみたのが下の図です。

２つの軸は緑色の斜めの線で示した面で接します。2つの赤い矢印の位置を絶えず一致するようにすれば、2つの軸は同じ速度で回転することになります。この図の通りの機構を実現しようとすると、折れ曲がっている軸の内側に注目している位置が来たときは軸が縮み、（上図の水平軸の\(l_2\))、軸の外側に来たときは軸が伸びる（上図の水平軸の\(l_1\))ような機構をつくらなければなりません。このような「回転に応じて伸び縮みする」ような機構をリーズナブルなコストで作るのはきわめて大変なこととなります。

ユニバーサルジョイントは、下図のように、２つの軸が90度で交差する十字型の部品１つと、2つのフォーク型の部品とを組み合わせて、折れ曲がって回転することができる軸を簡単に実現することができます。

実際の回転する様子を示す動画がWikipediaに記載されています。

ユニバーサルジョイントをつなげて一方の軸を傾けた状態を真横から見たのが下の図です。十字型の部品の軸の一方の先端は、赤で示した水平面上の線の上を移動します。他方の軸のの先端は、青で示した、水平面に対して傾いた面の上を移動します。

この中には、最初の図に示した、2つの軸が接合する緑の面に相当するものは存在しません。2つの軸の十字の先端が、どのような座標位置となるか、今回の興味の対象となります。

余談となりますが、等速ジョイントとしてWikipediaに紹介されているZeppa Jointは、２つの軸の交差する位置に、黄色な小さなボールを入れており、これらのボール群がなす軌跡が、最初の図の緑の線で示した接合面を実現していると考えることができます。

 

dda40xさんのBlogでたびたび取り上げられるユニバーサルジョイントの使い方ですが、阿里山のShayが間違っているらしいということにはびっくりしました。

ユニバーサルジョイントの不等速性については、すでにdda40xさんがわかりやすい動画を紹介され、また、創意工夫にあふれたT氏の説明の動画もあります。

(参考1) dda40xさんが紹介された動画

(参考2) T氏による動画―その１

(参考3) T氏による動画―その2

このような中、私などが出る幕などないのですが、このユニバーサルジョイントの不等速性は、高校一年生の数学、具体的には三角関数とベクトルの基礎がわかれば、数式で導出することができます。実は英語版のWikipediaには記載されているのですが、日本語で説明したものはないようなので、いかに私なりの説明を試みてみます。

ユニバーサルジョイントの組み合わせ方に関して理解されない理由の１つが、「角速度」という日常生活ではなじみの薄い概念で説明されているかではないか、と思っています。

我々はよく使うのは速度という概念です。ある速度\(v\)で動く物体があった時に、時間\(t\)経過したときに動いた距離は、それらの掛け算\(v \times t\)で求めることができます。従って、２つの物体が同じ場所から同じ時刻に同じ速度で移動を始めた場合、これらの２つの物体の移動開始からの移動距離は絶えず同じである、ということです。スタートから同じ速度で競争している２人のマラソン選手が絶えず同じ位置で竸り合っている、という状態がこれにあたります。

角速度は、回転運動するものが単位時間あたりに回転する角度と定義されます。角速度\(\omega\)が与えられたときに、ある時間\(t\)が経過したときに、その間に回転した角度は\(\omega \times t\)で求めることができます。

先ほどはマラソンで説明しましたが、こちらはトラック競技に例えると近いかと思います。半径\(r\)の真円のトラックを想定すると、選手が速度\(v\)でスタートしたとすると、レース開始から\(t\)経過した時点で、この選手の移動した距離は\(v \times t\)となります。ところで、トラックの一周の距離は\( 2\times r\times \pi\)ですから、スタートした位置を0度した時に、\(\frac{v\times t}{2\pi r}\times 360\)が、トラックを何度回ったか、が計算できます。単位時間で考えると、

\(\frac{v}{2\pi r}\times 360\)

が、この選手の角速度となります。ざっくりいうと、角速度とは、回転運動するものの速度を距離の代わりに角度で表現したものであり、本質的には速度と等価であると言えます。

従って、二人の選手が同じ速度で競争を始めたとすると、この二人の選手は同じ角速度で競争を行っていると言えます。同じ速度であると、絶えず移動距離は同じであり、絶えず同じ角度にいます。

つまり、「２つの軸が同じ角速度で回転していれば、絶えず同じ角度だけ回転している」はずであり、逆に言うと「2つの軸が同じ角速度でなければ、2つの軸の回転した角度が異なることがある」ということです。そこで、まずは角速度ではなく、ユニバーサルジョイントでつながれた軸の角度がどうなるか、ということを見てゆきます。

参考までに、上に書いたことを簡単な図としてみました。上は、2人がマラソンでが競争している様子です。二人の速度が同じであれば(\(v_1=v_2\))であれば、どの時間でも2人のランナーは同じ場所にいます。下は、2人がトラックで競争している様子です。二人の角速度が同じ(\(\omega_1=\omega_2\))であれば、どの時間でも二人のランナーは同じ角度の位置にいます。