dda40xさんのBlogでたびたび取り上げられるユニバーサルジョイントの使い方ですが、阿里山のShayが間違っているらしいということにはびっくりしました。

ユニバーサルジョイントの不等速性については、すでにdda40xさんがわかりやすい動画を紹介され、また、創意工夫にあふれたT氏の説明の動画もあります。

(参考1) dda40xさんが紹介された動画

(参考2) T氏による動画―その１

(参考3) T氏による動画―その2

このような中、私などが出る幕などないのですが、このユニバーサルジョイントの不等速性は、高校一年生の数学、具体的には三角関数とベクトルの基礎がわかれば、数式で導出することができます。実は英語版のWikipediaには記載されているのですが、日本語で説明したものはないようなので、いかに私なりの説明を試みてみます。

ユニバーサルジョイントの組み合わせ方に関して理解されない理由の１つが、「角速度」という日常生活ではなじみの薄い概念で説明されているかではないか、と思っています。

我々はよく使うのは速度という概念です。ある速度\(v\)で動く物体があった時に、時間\(t\)経過したときに動いた距離は、それらの掛け算\(v \times t\)で求めることができます。従って、２つの物体が同じ場所から同じ時刻に同じ速度で移動を始めた場合、これらの２つの物体の移動開始からの移動距離は絶えず同じである、ということです。スタートから同じ速度で競争している２人のマラソン選手が絶えず同じ位置で竸り合っている、という状態がこれにあたります。

角速度は、回転運動するものが単位時間あたりに回転する角度と定義されます。角速度\(\omega\)が与えられたときに、ある時間\(t\)が経過したときに、その間に回転した角度は\(\omega \times t\)で求めることができます。

先ほどはマラソンで説明しましたが、こちらはトラック競技に例えると近いかと思います。半径\(r\)の真円のトラックを想定すると、選手が速度\(v\)でスタートしたとすると、レース開始から\(t\)経過した時点で、この選手の移動した距離は\(v \times t\)となります。ところで、トラックの一周の距離は\( 2\times r\times \pi\)ですから、スタートした位置を0度した時に、\(\frac{v\times t}{2\pi r}\times 360\)が、トラックを何度回ったか、が計算できます。単位時間で考えると、

\(\frac{v}{2\pi r}\times 360\)

が、この選手の角速度となります。ざっくりいうと、角速度とは、回転運動するものの速度を距離の代わりに角度で表現したものであり、本質的には速度と等価であると言えます。

従って、二人の選手が同じ速度で競争を始めたとすると、この二人の選手は同じ角速度で競争を行っていると言えます。同じ速度であると、絶えず移動距離は同じであり、絶えず同じ角度にいます。

つまり、「２つの軸が同じ角速度で回転していれば、絶えず同じ角度だけ回転している」はずであり、逆に言うと「2つの軸が同じ角速度でなければ、2つの軸の回転した角度が異なることがある」ということです。そこで、まずは角速度ではなく、ユニバーサルジョイントでつながれた軸の角度がどうなるか、ということを見てゆきます。

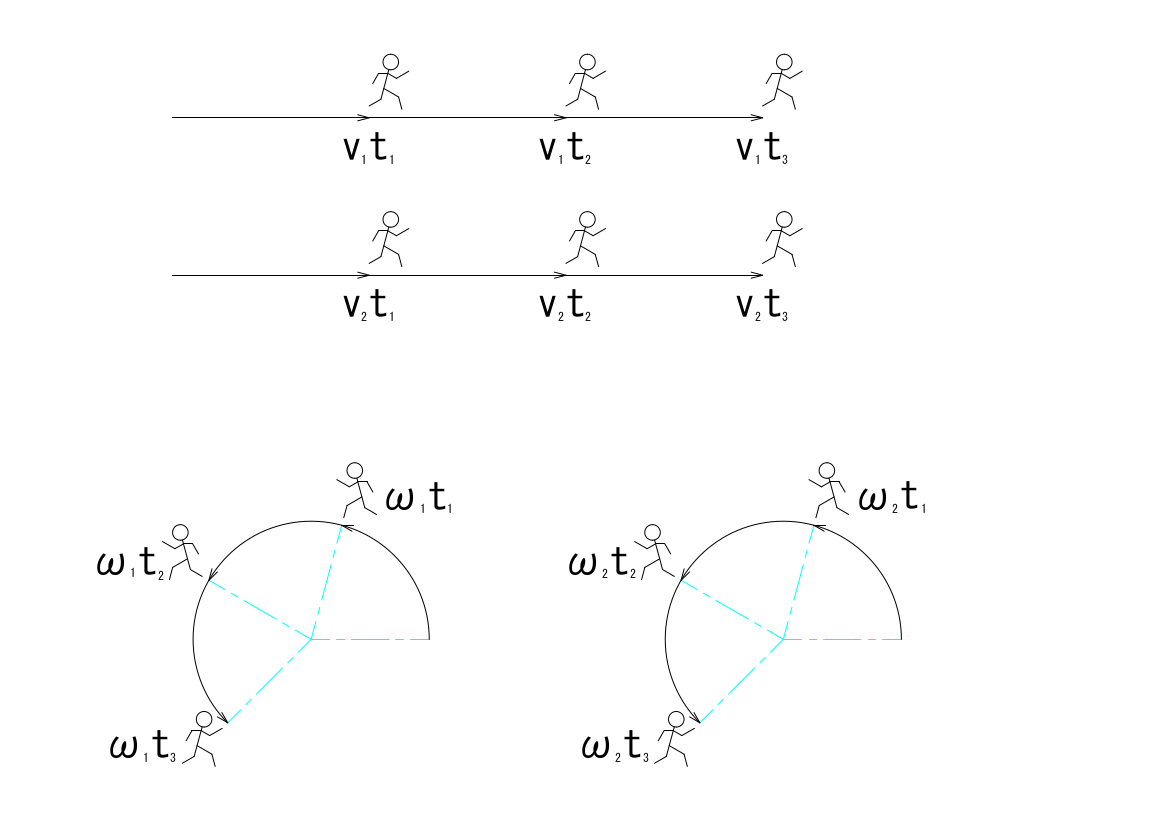
参考までに、上に書いたことを簡単な図としてみました。上は、2人がマラソンでが競争している様子です。二人の速度が同じであれば(\(v_1=v_2\))であれば、どの時間でも2人のランナーは同じ場所にいます。下は、2人がトラックで競争している様子です。二人の角速度が同じ(\(\omega_1=\omega_2\))であれば、どの時間でも二人のランナーは同じ角度の位置にいます。