長々と続けてきた、ユニバーサルジョイントの正しい使い方のシリーズの目次をこちらに用意しておきます。今読み返すと書き足りないと思うこともありますが、追々直してゆきたいと思っています。またグラフの表示のプラグインの改訂により、当初の表示が乱れているところもありますが、こちらも直してゆきます。

また、同じ内容を固定ページにも用意しておきます。

（１） – はじめに

（２） – 折れ曲がった軸が回転するとはどういうことか

（３） – 三角関数の復習

（４） – 基準点の座標を求める

（５） – 基準点のなす角度の関係を求める

（６） – ２つのジョイントを組み合わせる

（７） – 作図で理解する

（８） – 簡易型ユニバーサルジョイントの解析

（９） – 簡易型ユニバーサルジョイントを２つ組み合わせる

（１０） – 簡易型ユニバーサルジョイントを正規型ユニバーサルジョイントと比較する

（１１） – 角速度を計算する

（１２） – ユニバーサルジョイントを2つ組み合わせた際の角速度を計算する

（１３） – 具体的な数値をあてはめてみる

（１４） – α=βとなる条件を改めて考える

（１５） – αとβとの関係の一例を考える

（１６） – MPギアを例に |α|≠|β|の場合の具体的な数値を当てはめる

（１７） – Shayの場合のαとβとの関係を考える

（１８） – Shayのαとβとの具体的な数値をあてはめる

（１９） – 阿里山のShayのαとβとの具体的な数値をあてはめる

（２０） – 3つの軸が同一平面に存在しない場合を考える

（２１） – ２つのベクトルのなす角度と外積

（２２） – ２つのベクトルのなす角と外積とを使って解析に必要な角度を求める

（２３） – 3つの軸が同一平面に存在しない場合の角速度の変動（MPギアの場合）

（２４） – 3つの軸が同一平面に存在しない場合の角速度の変動（MPギアの場合-モーターの左右のジョイントの角速度の変動の解析）

（２５） – 3つの軸が同一平面に存在しない場合の角速度の変動（Shayの場合）

（２６） – まとめ

（２７） – MPギアの左右の角速度の差について

（２８） – MPギアの左右の角速度の比を計算する

（２９） – MPギアの左右の角速度の比についてのまとめ

（３０） – まとめ（修正版）

4回前の記事でまとめをしてこのシリーズは完結するはずでしたが、考慮すべき事ができ、3回ほど記事を続けました。今回がたぶん本当のまとめになると思います。前回のまとめと重複する部分がほとんどですが、このシリーズで考察してきた事を、改めて以下にまとめます。

（１）まずはユニバーサルジョイントの使い方一般について。

• ユニバーサルジョイントが折れ曲がって回転する場合、角速度の変動が発生するので、必ず2つ組み合わせること。その際に、２つのユニバーサルジョイントをつなぐ軸のピンの向き（位相）を同じにそろえること。
• ピンの向きを揃えた場合、最初のユニバーサルジョイントで発生した角速度の変動を、2つ目のユニバーサルジョイントが打ち消す方向に働く（２つのジョイントの角度が同じであれば完全に打ち消される）。
• ピンの向きを揃えない場合（90度ずれている場合）、1つ目のユニバーサルジョイントで発生した角速度の変動を、2つ目のユニバーサルジョイントが増幅する方向に働く。

（２）模型では、簡易型のユニバーサルジョイントがよく使われます。こちらについても解析を行い、次の結果を得ました。

• 簡易ユニバーサルジョイントは、正規型ユニバーサルジョイントと等価である。
• 従って、正規型ユニバーサルジョイントの場合と同様、２つのユニバーサルジョイントをつなぐ軸のピンの向き（位相）をそろえることが必要。

（３）日本型の電車を中心に、MPギア（もしくはそれに類似する形態の駆動系、以下MPギアで代表）がよく用いられています。こちらの考察を進め、次のような結論や仮説を得ました。

• ２つのジョイントの曲がる角度は一致しないので、MPギアでは角速度の変動は必ず発生する。
• 角速度の変動を低減するには、次のようなことが有効。
  １）モーターは必ず中央に置きジョイントの位置が左右対称になるようにする。
  ２）可能な限り短いモーターを選ぶとともに、モーター側のユニバーサルジョイントは、可能な限り中央に寄せる。
• （仮説）角速度の変動が5%に近づくあたりから、車両の挙動に影響を与える可能性が高い。　←　この仮説は一旦取り下げます。
• モーターの軸に装着するユニバーサルジョイントの位相を必ずそろえること。さもなくが、モーターの左右のユニバーサルジョイントの角速度差が発生する。

（４）ユニバーサルジョイントを構成する3つの軸が同一平面にない場合の解析も行いました。その結果次の結論を得ました。

• ユニバーサルジョイントの軸が3つの軸が同一平面にない場合は、3つの軸が同一平面上にある場合に比べ、角速度の変動を大きくする方向に働く。
• 従って、ユニバーサルジョイントを構成する3つの軸は同一平面上に置く。

最初に述べた、ピンの向きを揃える、を念のため下に図示します。

下は誤った使い方の図です。

ユニバーサルジョイントのモータへの正しい取り付け方も図示します。

誤った取り付け方を下に示します。

それでは、長々と続いてきたシリーズを終わりにしたいと思います。

このシリーズを続けるに当たって、示唆をいただいた方、貴重な情報をいただいた方に改めて御礼申し上げます。ありがとうございました。

前回、前々回と、MPギアのような駆動系でモーターの左右にユニバーサルジョイントで動力を伝道する場合に、モーターに取り付けるユニバーサルジョイントの位相が揃っていないと(\(\Delta\neq 0\))、左右のユニバーサルジョイントの最終伝達面の角速度が異なる、というを明らかにし、\(\Delta=\frac{\pi}{2}\)の場合を計算するとその左右の角速度比の変動が最大になり、かつかなり大きな値になるということを示しました。

これを踏まえてこれまでの議論を整理すると、MPギアを使った車両がカーブを走行する際には、２つの角速度の変動が車両の挙動に影響を与えることが考えられます。

１つめは、ユニバーサルジョイント単体で発生する角速度の変動です。カーブでは、ユニバーサルジョイントの折れ曲がり方が同じではない(\(\alpha\ne\beta\))ので、この変動は避けられません。しかしながら、ユニバーサルジョイントの位相をそろえる(\(\delta=0\)とする)ことで、この変動を最低限にすることができます。

そして、２つめは、今回議論したように、モーターに取り付ける2つのユニバーサルジョイントの位相が揃っていないことによって発生する、左右のユニバーサルジョイントの最終伝達面の角速度の差です。つまり、最終的な車輪の回転速度が左右の台車で異なる、ということです。これは\(\Delta=0\)とすることで防げますので必ず守るべきであると言えます。念のため、前々回掲載した図で言えば、左のような取り付け方法をとらなければならない、ということです。

定性的には、前者は車両の速度が一定しない（脈動する）ことに、後者は前後の台車の速度が異なる事による効率の低下やスムーズではない挙動に、つながると考えます。

以前MPギアの解析を行ったときにたてた、「角速度の変動率が5%に近づくあたりから、スムーズな走行に影響を与える」という仮説は\(\Delta=0\)であった場合にのみ成り立つものです。仮に\(\Delta=\frac{\pi}{2}\)であったとすると、角速度の変動率が8%を超えるあたりから、ということが言えるかと思いますが、2つの角速度の変動のうちどちらが支配的な影響を与えるか、については実験を行わないとわからないと思います。

いずれにしても、上記の仮説は一旦取り下げることといたします。

前回の記事で、モーターの左右に取り付けるユニバーサルジョイントに関し、その取り付け部分の位相\(\Delta\)を揃えておかないと、左右のユニバーサルジョイントの最終的な角速度に差が出ることを示しました。

実際にどれくらいの差が出るかを、以前解析に用いたモハ185を題材として計算してみます。まず、前回の計算結果のグラフを再掲します。半径600mmと500mmとで、ユニバーサルジョイントの位相が正しい(\(\delta=0\))場合と、間違っている(\(\delta=\frac{\pi}{2}\))場合の角速度の変動を示したものです。

\(\Delta=0\)の場合は、\(\delta=0\)、\(\delta=\frac{\pi}{2}\)にかかわらず、左右の角速度は同じという結論を前回の議論で得ましたので、以下では\(\Delta=\frac{\pi}{2}\)、つまりモーターに取り付けられたユニバーサルジョイントの位相が90度ずれている場合を考えます。

まず、R600で\(\delta=0\)の場合、左右の角速度の比がどうなるかを示したのが下図です。左側のユニバーサルジョイントの角速度比、右側のユニバーサルジョイントの角速度比も併せて示します。

このグラフを見てわかることは、左側のユニバーサルジョイントの角速度の変動、右側のユニバサールジョイントの角速度の変動は以前求めたものと全く同じもので、ユニバーサルジョイントに取り付ける側のジョイントの位相が\(\frac{\pi}{2}\)(90度)ずれていることで、グラフも\(\frac{\pi}{2}\)ずれています。その結果、左側の角速度比が最大（最小）になる時に、右側の角速度比が最小（最大）になります。ユニバーサルジョイント単体の角速度の変動は±3%弱に抑えられていますが、左右の角速度比は±6%程度になることがわかります。

次にR500で\(\delta=0\)の場合のグラフを示します。

カーブが急になったことで、ユニバーサルジョイント単体の角速度の変動は±4%程度になり、左右の角速度の比は±8%程度となっています。

\(\delta=\frac{\pi}{2}\)の時、ユニバーサルジョイント単体の位相が90度ずれている場合、ユニバーサルジョイント単体の角速度の変動が大きくなりますので、更に条件が悪くなることが考えられます。R600の場合、R500の場合のグラフを続けて示します。

R600の場合にユニバーサルジョイント単体の角速度比の変動が±4%程度のものが左右比で±9%程度までに拡大すること、R500の場合はユニバーサルジョイント単体の角速度比の変動が±6%程度のものが左右比で±13%程度までに拡大すること、がわかります。

ここまで、\(\Delta=\frac{\pi}{2}\)の場合を考えましたが、先ほど議論した通り\(\Delta\ne 0\)の時は、左右の角速度の変動が\(\Delta\)分ずれるので、左右のユニバーサルジョイントの角速度比の変動が必ず発生します。

わざわざ示すまでもないかもしれませんが、\(\Delta=\frac{\pi}{6}\)(30°)、\(\Delta=\frac{\pi}{3}\)(60°)、\(\Delta=\frac{\pi}{2}\)(90°)、のそれぞれの場合に、左右のユニバーサルジョイントの角速度比がどう変わるかを、R600の場合とR500の場合とについて示します。

長くなったので、今回の結論は次回にまとめます。

前回のまとめの投稿で、本質的に書くべきことはすべて網羅したと大見えを切りましたが、マーフィーの法則よろしく、一つ重要なことを見落としていたことに気づきました。

MPギアの解析の際に、「左右対称なので、同じ条件で解析できる」ということを述べました。確かに、左右のそれぞれのユニバーサルジョイント単体の挙動は同じ条件で解析できるのですが、そもそもモーターの左右のユニバーサルジョイントのモーター側の基準点の位相が揃っているか、を考慮しなければなりませんでした。

ここまでの議論は、下図左側に示したように、モーター側のジョイントの位相が揃っていることを前提にしたものでした。しかしながら、下図右側に示したように、この位相が揃っていない場合も考えられます。今回は、この位相差\(\Delta\)がモーターの左右ユニバーサルジョイントの最終伝達面の角速度にどのような影響を与えるかを解析してみます。

今回の議論では、通常のＭＰギア、つまりジョイントは完全に左右対称の位置にあり、3つの軸が同一平面上にある場合についてのみ議論します。Shayのようにジョイントの位置が左右対称にない場合、ユニバーサルジョイントを構成する3つの軸が同一平面上にない場合、についても同様の議論が成り立ち、同じ傾向と示すと考えられます。

モータに向かって左側のユニバーサルジョイントの駆動面の基準点が角速度\(\omega\)で回転する場合、\(\omega\)に対する最終伝達面の角速度の比は、以前求めたように

\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

で計算できます。

左側のユニバーサルジョイントの回転方向に向かって、右側のユニバーサルジョイントの駆動面の基準点の位相が、\(\Delta\)進んでいるとします。右側のユニバーサルジョイントの角速度は\(-\omega\)となりますので、右側のユニバーサルジョイントの最終駆動面の角速度比は次の式で表すことができます。なお議論を簡単にするために、\(\delta\)は、左右のユニバーサルジョイントで同じ、つまり左右のユニバーサルジョイントの位相はどちらも正しい、あるいはどちらも間違っている、ということを前提とします。

\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(-\omega t-\Delta)+sin^2(-\omega t-\Delta)\cdot {cos}^2(\alpha) – (cos(-\omega t-\Delta)\cdot cos(\delta)-sin(-\omega t-\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

\(cos(-x)=cos(x)\)、\(sin(-x)=-sin(x)\)ですので、上記の式は

\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(\omega t+\Delta)+sin^2(\omega t+\Delta)\cdot {cos}^2(\alpha) – (cos(\omega t+\Delta)\cdot cos(\delta)+sin(\omega t+\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

となります。

これらの2つの式から、左側のユニバーサルジョイントの最終伝達面の角速度に対する右側の加速度ユニバーサルジョイントの最終伝達面の角速度の比は

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t+\Delta)+sin^2(\omega t+\Delta)\cdot {cos}^2(\alpha) – (cos(\omega t+\Delta)\cdot cos(\delta)+sin(\omega t+\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

で表すことができます。

この式は、動力の左右にユニバーサルジョイントで動力を伝動する場合、左右それぞれのユニバーサルジョイントで発生する角速度の変動に加え、左右のユニバーサルジョイントの最終伝達面の角速度の差が発生しうる、ということを言っています。これは、どちらか一方の動力が速く（遅く）回転しようとしているのに、一方の動力はそれを妨げる方向に働くということを意味しており、この比が大きいと、動力伝達の効率を低下させ、スムーズな挙動に影響があると考えられます。

前回までの議論では、\(\Delta=0\)を前提としているのでした。これを上記に代入すると

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

となります。いつものように、我々の興味のあるのは、\(\delta=0\)、もしくは\(\delta=\frac{\pi}{2}\)の場合です。

\(\delta=0\)の時、\(sin(\delta)=0\)、\(cos(\delta)=1\)ですので、上記の式は、

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta))^2\cdot{sin}^2(\beta)}=1\)

となります。また、\(\delta=\frac{\pi}{2}\)の時、\(sin(\delta)=1\)、\(cos(\delta)=0\)ですので、上記の式は、

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (-sin(\omega t)\cdot cos(\alpha))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (sin(\omega t)\cdot cos(\alpha))^2\cdot{sin}^2(\beta)}=1\)

となります。従って、\(\Delta=0\)の時、ユニバーサルジョイントの左右の最終伝達面の角速度比は同じであるということが確認できました。この結果は、\(\Delta=0\)の時、左右の挙動は左右対称で同じに解析できるという、これまで暗黙に仮定を置いてきたことを裏付けるものです。

\(\Delta=\frac{\pi}{2}\)とすると、ユニバーサルジョイントの左右の最終伝達面の角速度比は、

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t+\frac{\pi}{2})+sin^2(\omega t+\frac{\pi}{2})\cdot {cos}^2(\alpha) – (cos(\omega t+\frac{\pi}{2})\cdot cos(\delta)+sin(\omega t+\frac{\pi}{2})\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

\(sin(\frac{\pi}{2}\pm\theta)=cos(\theta)\)、\(cos(\frac{\pi}{2}\pm\theta)=\mp sin(\theta)\)、ですので、

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) – (sin(\omega t)\cdot cos(\delta)-cos(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

となります。

\(\delta=0\)の時、上記の式は

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – {cos}^2(\omega t)\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) – {sin}^2(\omega t)\cdot{sin}^2(\beta)}\)

となり、\({sin}^2(\theta)+{cos}^2(\theta)=1\)を利用すると

\(\frac{cos^2(\omega t)\cdot{cos}^2(\beta)+sin^2(\omega t)\cdot {cos}^2(\alpha)}{sin^2(\omega t)\cdot{cos}^2(\beta)+cos^2(\omega t)\cdot {cos}^2(\alpha)}\)

と整理できます。

\(\delta=\frac{\pi}{2}\)の時、上記の式は

\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – {sin}^2(\omega t)\cdot {cos}^2(\alpha)\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) -{cos}^2(\omega t)\cdot{cos}^2(\alpha)\cdot{sin}^2(\beta)}\)

\(=\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha)\cdot{cos}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha)\cdot{cos}^2(\beta)}\)

となります。

これらの2つの式は、\(\Delta=\frac{\pi}{2}\)の場合、左右の動力で角速度の差が確実に発生するということを言っています。

次回は、どの程度の角速度の差が左右で発生するかをこれらの式に具体的な数字を入れて見てみたいと思います。

この投稿は、加筆修正いたしましたので、こちらをご覧になってください。

長々と続けてきたシリーズ、書き足りないこともあるとは思っていますが、本質的に書くべきことはすべて網羅したと考えていますので、今回でいったん区切りをつけることとします。

ここまで考察してきたことを以下にまとめます。

（１）まずはユニバーサルジョイントの使い方一般について。

• ユニバーサルジョイントが折れ曲がって回転する場合、角速度の変動が発生するので、必ず2つ組み合わせること。その際に、２つのユニバーサルジョイントをつなぐ軸のピンの向き（位相）を同じにそろえること。
• ピンの向きを揃えた場合、最初のユニバーサルジョイントで発生した角速度の変動を、2つ目のユニバーサルジョイントが打ち消す方向に働く（２つのジョイントの角度が同じであれば完全に打ち消される）。
• ピンの向きを揃えない場合（90度ずれている場合）、1つ目のユニバーサルジョイントで発生した角速度の変動を、2つ目のユニバーサルジョイントが増幅する方向に働く。

（２）模型では、簡易型のユニバーサルジョイントがよく使われます。こちらについても解析を行い、次の結果を得ました。

• 簡易ユニバーサルジョイントは、正規型ユニバーサルジョイントと等価である。
• 従って、正規型ユニバーサルジョイントの場合と同様、２つのユニバーサルジョイントをつなぐ軸のピンの向き（位相）をそろえることが必要。

（３）日本型の電車を中心に、MPギア（もしくはそれに類似する形態の駆動系、以下MPギアで代表）がよく用いられています。こちらの考察を進め、次のような結論や仮説を得ました。

• ２つのジョイントの曲がる角度は一致しないので、MPギアでは角速度の変動は必ず発生する。
• 角速度の変動を低減するには、次のようなことが有効。
  １）モーターは必ず中央に置きジョイントの位置が左右対称になるようにする。
  ２）可能な限り短いモーターを選ぶとともに、モーター側のユニバーサルジョイントは、可能な限り中央に寄せる。
• （仮説）角速度の変動が5%に近づくあたりから、車両の挙動に影響を与える可能性が高い。

（４）ユニバーサルジョイントを構成する3つの軸が同一平面にない場合の解析も行いました。その結果次の結論を得ました。

• ユニバーサルジョイントの軸が3つの軸が同一平面にない場合は、3つの軸が同一平面上にある場合に比べ、角速度の変動を大きくする方向に働く。
• 従って、ユニバーサルジョイントを構成する3つの軸は同一平面上に置く。

最初に述べた、ピンの向きを揃える、を念のため下に図示します。

下は誤った使い方の図です。

このシリーズは、7回目を書いた時点で終わる予定でしたが、次々と考えるべきことが出てきて、私自身の興味もつきず、なんと25回も続けてしまいました。数式ばかりの記事に辟易した人が多かったのではないかと思いますが、これは厳密な議論をすることを目的としたものですので、ご了解ください。さび付いた頭で三角関数やら微分やらベクトルやらと格闘するのは大変でしたが、久しぶりに数学の奥深さを感じたように思います。何度か検証したので誤りはないのではないかと思っていますが、もしもお気づきの点があれば、ご指摘頂ければ幸いです。

ここまで、いろいろな方に示唆をいただき、また貴重な情報をいただきました。個別にお名前を挙げることはしませんが、深く御礼申し上げます。

前々回、前回と、ユニバーサルジョイントの3つの軸が同一平面に存在しない場合を仮定して、角速度がどのように変動するかの具体例をMPギアを例として計算してみました。今回はこれをShayの場合で考察してみます。解析の対象としたのは、前に紹介したGreenbrier, Cheat and Elk Railroadの12号機（おそらくsn3156)です。

1922年版のLocomotive cyclopedia of American practiceに載っている主要寸法を次の図に示します。

この150tのShayは、以前紹介したWestern MarylandのShayに匹敵する最大級のShayです。Western Marylandと同じく、最小半径は22度のであると仮定して議論を進めます。

まずは解析に必要な座標を計算します。駆動軸が平面にあるShayの座標の考え方に、上記の軸の高さを考慮したものが次のようになります。なお、これまでは駆動軸がカーブの内側にある場合と外側にある場合との両方を考えてきましたが、今回は条件の厳しい、カーブの内側にある場合のみを考慮することとします。

エンジンに向かって左側のユニバーサルジョイントの角速度の解析に必要な座標は、\(\theta=cos^{-1}(\frac{w}{r})\)とすると、

\(A=(0, -r\cdot sin(\theta)-{l_3}, h)\)

\(B=(-{l_1}, r\cdot sin(\theta)-{l_3}, h)\)

\(C=(-w+{l_3}\cdot cos(\theta)+{l_2}\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}\cdot cos(\theta),0)\)

\(D=(-w+{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)

となります。

求める角速度比を得るには、\(\vec{AB}\)と\(\vec{BC}\)とのなす角\(\alpha\)、\(\vec{BC}\)と\(\vec{CD}\)とのなす角\(\beta\)、\(\vec{AB}\)と\(\vec{BC}\)との外積\(\vec{AB}\times\vec{BC}\)に対して\(\vec{BC}\)と\(\vec{CD}\)との外積\(\vec{BC}\times\vec{CD}\)がどれだけ回転してるかの角度\(\eta\)を求め、

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)

を計算します。

Shayの場合は、エンジンの左側と右側とで寸法が異なることが大半ですので、右側の角速度比は左側と同様の計算方法で別途求める必要があります。まずはエンジンに向かって右側のユニバーサルジョイントの解析に必要な座標は、

\(A’=(0, -r\cdot sin(\theta)-{l_3}, h)\)

\(B’=(-{l_1}’, r\cdot sin(\theta)-{l_3}, h)\)

\(C’=(w-{l_3}\cdot cos(\theta)-{l_2}’\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}’\cdot cos(\theta),0)\)

\(D’=(w-{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)

となります。

これの座標から、\(\vec{A’B’}\)と\(\vec{B’C’}\)とのなす角\(\alpha’\)、\(\vec{B’C’}\)と\(\vec{C’D’}\)とのなす角\(\beta’\)、\(\vec{A’B’}\)と\(\vec{B’C’}\)との外積\(\vec{A’B’}\times\vec{B’C’}\)に対して\(\vec{B’C’}\)と\(\vec{C’D’}\)との外積\(\vec{B’C’}\times\vec{C’D’}\)がどれだけ回転してるかの角度\(\eta’\)を求めます。

前回触れたように、エンジンの左側の角速度を\(\omega\)とした場合、右側の角速度は\(-\omega\)となりますので、求める角速度比は

\(\frac{cos(\alpha’)\cdot cos(\beta’) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha’) – (cos(\omega t)\cdot cos(\delta-\eta’)+sin(\omega t)\cdot cos(\alpha’)\cdot sin(\delta-\eta’))^2\cdot{sin}^2(\beta’)}\)

となります。

得られた計算式で、位相が正しい場合と、位相が間違っている場合との角速度の変動を計算した結果を次のグラフに示します。

比較のために、エンジンの中心軸が、台車の軸と水平になった(h=0)場合のグラフと重ねてみたものを示します。

これで見る限り、h=1.5”としても、1%を下回る角速度の変動となりますので、実用上は大きくは影響を与えないであろうということは言えるかと思います。少しでも高さを稼ぎたい理由があったのでしょうか。

いまさら言わなくても、という気がしますが、逆位相の場合に急激に変動が大きくなる傾向は、MPギアの時の計算結果と同じとなります。

前回は、3つの軸が同一平面に存在しない場合の角速度の変動を、MPギアの場合を例にとってまとめました。MPギアは、車体の中心で左右対称という構成となっていますので、モーターの左右にあるユニバーサルジョイントは同じ挙動を示すであろうということが想像できますが、この点について明確にしておきたいと思います。

まず、MPギアに使われるユニバーサルジョイントの座標を改めて次の図に示します。前回の図の\(A\)、\(B\)、\(C\)、\(D\)に加え、左右対称に\(A’\)、\(B’\)、\(C’\)、\(D’\)を示しました（ただし、\(A=A’\)）。

立体的に表現すると次のようになります。なお、この図を含めた以下の図は、ベクトルの角度および向きを示すことを目的としたものであり、ベクトルの長さは実際の値を反映したものではありません。

3つの軸が同一平面に存在しないユニバーサルジョイントの挙動を解析する際のポイントは、２つのベクトルのなす角と外積とを使って解析に必要な角度を求める、の記事で述べたように、\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta\)を求めることです。同様に\(\vec{A’B’}\times\vec{B’C’}\)と\(\vec{B’C’}\times\vec{C’D’}\)とのなす角\(\eta’\)を求めることで、モーターの左右にあるユニバーサルジョイントの挙動を解析することができます。これらを求めた結果の一例を次に図示します。

向きをそろえた図の方がわかりやすいと思いますので、これを下に示します。

この図からわかることは、\(\eta\)と\(\eta’\)とは、絶対値は同じとなりますが、符号は異なる、ということです。更に軸の回転方向も反対となりますので、左側のユニバーサルジョイントの駆動面の角速度を\(\omega\)とすると、右側のユニバーサルジョイントの駆動面は\(-\omega\)として考える必要があります。

これらをもとに、以前示した、駆動面に対する最終伝達面の角速度の比が、左と右とでどうなるかを考えてみます。

ユニバーサルジョイントの駆動面に対する最終伝達面の角速度の比は、次の式で表すことができるのでした。

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)

この式がモーターの左側のユニバーサルジョイントの最終伝達面の角速度の比を表すとすると、\(\omega\)と\(\eta\)との符号を反転させた式が右側のユニバーサルジョイントの最終伝達面の角速度の比を示す式となります。なお、\(\alpha\)、\(\beta\)については、絶対値のみを考えればよいことは以前に述べましたし、左右対称であることから、絶対値は一致しますので、以下の議論には影響を与えません。

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(-\omega t)+{sin}^2(-\omega t)\cdot {cos}^2(\alpha) – (cos(-\omega t)\cdot cos(\delta-(-\eta))-sin(-\omega t)\cdot cos(\alpha)\cdot sin(\delta-(-\eta)))^2\cdot{sin}^2(\beta)}\)

\(sin(-\theta)=-sin(\theta)\)、\(cos(-\theta)=cos(\theta)\)ですので、上記の式は、

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta+\eta))^2\cdot{sin}^2(\beta)}\)

となります。２つの式を見比べると、異なるのは分母の一部で、モーターの左側の角速度の比を示す式の

\(cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta)\)

と、モーターの右側の角速度の比を示す式の

\(cos(\omega t)\cdot cos(\delta+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta+\eta)\)

とになります。

我々の興味の対象は、いつものように、\(\delta=0\)の場合と、\(\delta=\frac{pi}{2}\)の場合とですので、それぞれの場合について、2つの式がどのようになるかを見てみます。

まず、\(\delta=0\)の場合ですが、左側の式は

\(cos(\omega t)\cdot cos(0-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(0-\eta)\)

\(=cos(\omega t)\cdot cos(\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\eta)\)

となり、右側の式は

\(cos(\omega t)\cdot cos(0+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(0+\eta)\)

\(=cos(\omega t)\cdot cos(\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\eta)\)

となり、両者は一致することがわかります。

\(\delta=\frac{\pi}{2}\)の場合、\(sin(\frac{\pi}{2}\pm\theta)=cos(\theta)\)、\(cos(\frac{\pi}{2}\pm\theta)=\mp sin(\theta)\)、という三角関数の性質を利用すると、左側の式は

\(cos(\omega t)\cdot cos(\frac{\pi}{2}-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\frac{\pi}{2}-\eta)\)

\(=cos(\omega t)\cdot sin(\eta)-sin(\omega t)\cdot cos(\alpha)\cdot cos(\eta)\)

右側の式は、

\(cos(\omega t)\cdot cos(\frac{\pi}{2}+\eta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\frac{\pi}{2}+\eta)\)

\(=-(cos(\omega t)\cdot sin(\eta) – sin(\omega t)\cdot cos(\alpha)\cdot cos(\eta))\)

となり、左側の式の符号を反転した値となります。

ここで元の式の分母を見ると、この項は2乗されますので、結果的に左の式と右の式とは同じ結果となることがわかります。

まとめると、MPギアのようにユニバーサルジョイントが左右対称に構成され、一定半径の曲線を走行する場合は、モーターの左右のユニバーサルジョイントの最終駆動面の角速度の変動は左右で同じになる、ということが今回の結論です。

ユニバーサルジョイントの3つの軸が平面にない場合の角速度の変動を前回求めました。簡単におさらいすると、3つの軸が同一平面上にあり、駆動面の角速度を\(\omega\)としたときの最終伝達面の角速度

\(\frac{d\xi}{dt}= \frac{\omega\cdot cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)

において、\(\delta\)を\(\delta-\eta\)で読み替えたものが、最終伝達面の角速度となります。

従って、駆動面の角速度に対する最終伝達面の角速度の比は、

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)

で求められます。

今回は、MPギアの場合を例にとり、モーターの軸が台車の軸に対し、\(0mm\)から\(6mm\)まで、\(1.5mm\)刻みで高さが変化したときに、角速度比がどのように変化するかを計算します。

MPギアでは、3つの軸が同一平面に置かれることを想定していると理解しており、ここでの議論そのものに意味はないかと思いますが、全体の傾向を把握するために結果を示すものです。

まず、下の図に座標の求め方を記しました。曲線の中心\(O_r\)を原点とすると、\(A\)、\(B\)、\(C\)、\(D\)は、次のように計算することができます。三角関数が理解できていれば簡単に導出できますので、詳しい説明は省略します。

\(A = (0,r\cdot sin(\theta), h)\)

\(B=(-l_1, r\cdot sin(\theta), h)\)

\(C=(-w+l_2\cdot sin(\theta), r\cdot sin(\theta)+l_2\cdot cos(\theta), h)\)

\(D=(-w, r\cdot sin(\theta), h)\)

以前示したエンドウのモハ185の寸法において、600Rで角速度比がどのように変動するかを示したのが次のグラフです。

R=500の場合を示します。

いずれのグラフを見ても、\(h\)が増えると、角速度の変動の比率が急激に大きくなること、逆位相の場合は特に顕著に大きくなること、が分ります。

これまで繰り返してきた、「ユニバーサルジョイントは必ず同位相で使うこと」、に加え、「ユニバーサルジョイントは必ず同一平面上に存在するように高さを調整すること」、が必要であると言えます。

最後に、\(h\)の変動に伴って、\(\eta\)がどのように変動するかの図を参考に示します。

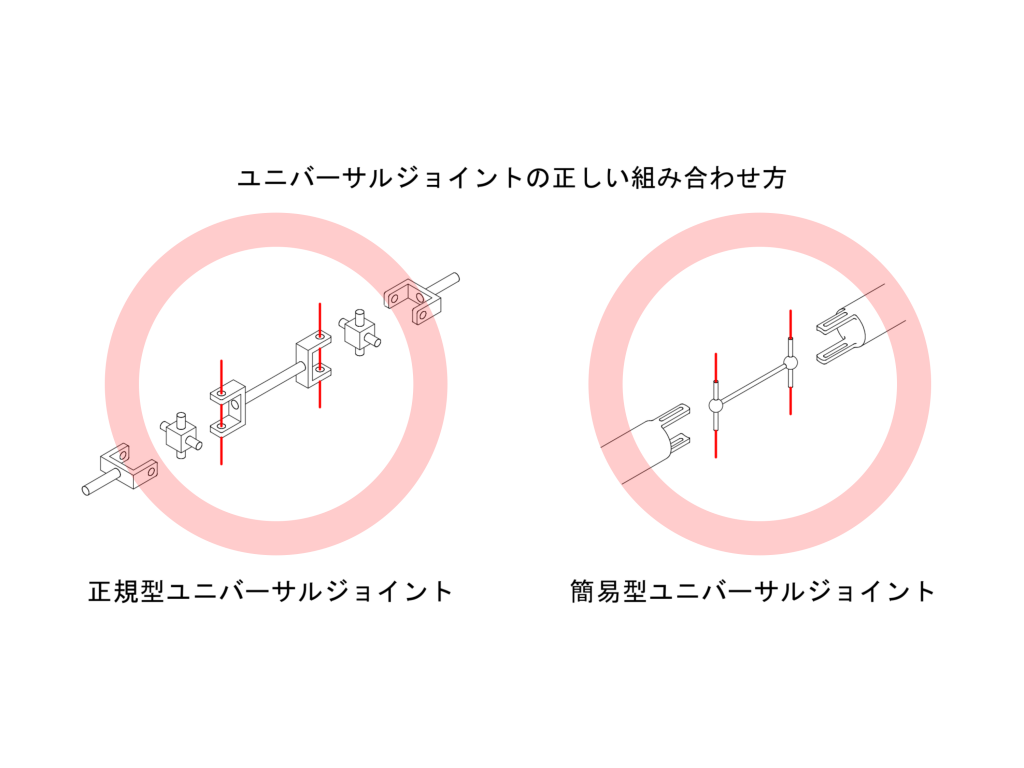
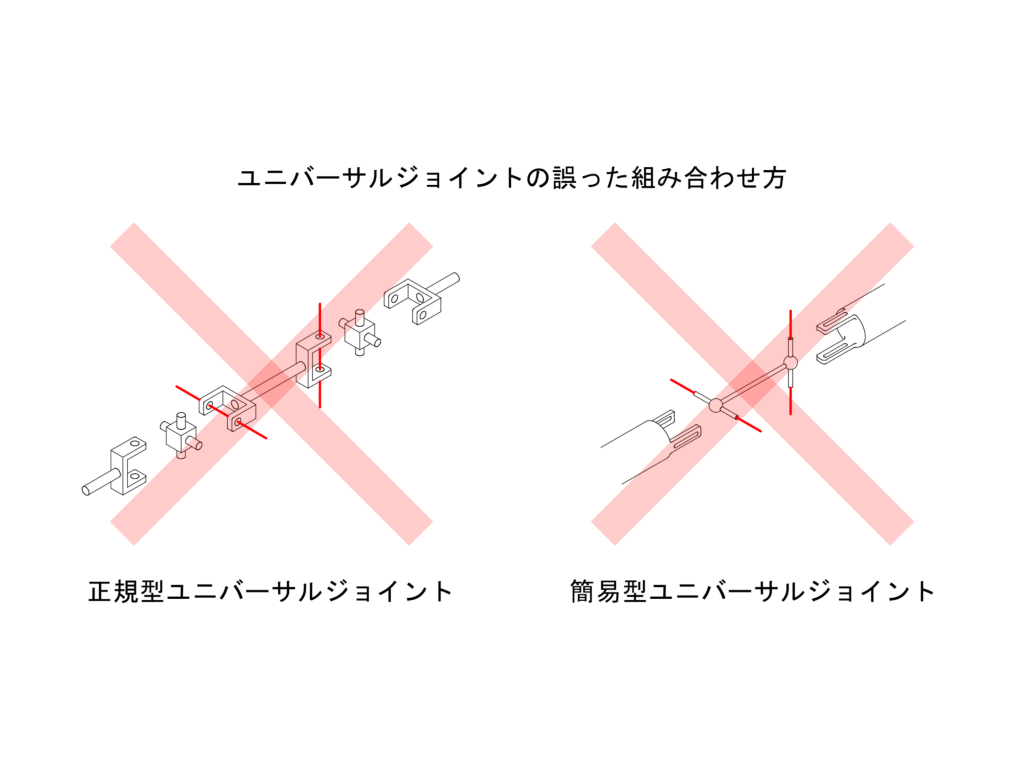
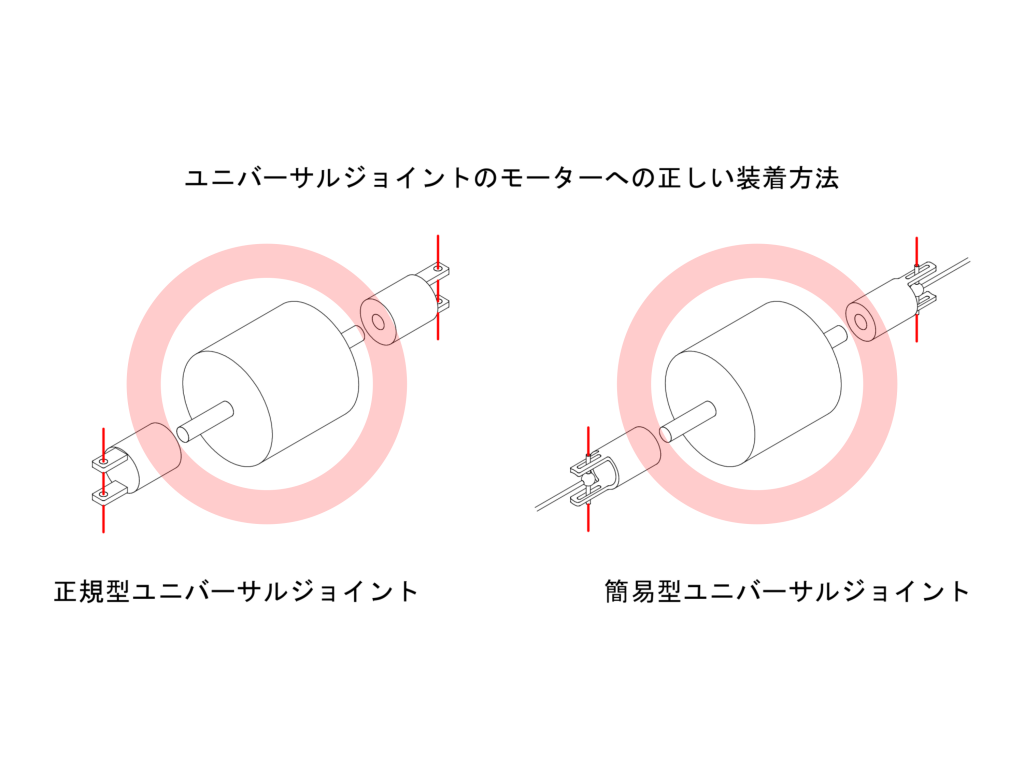
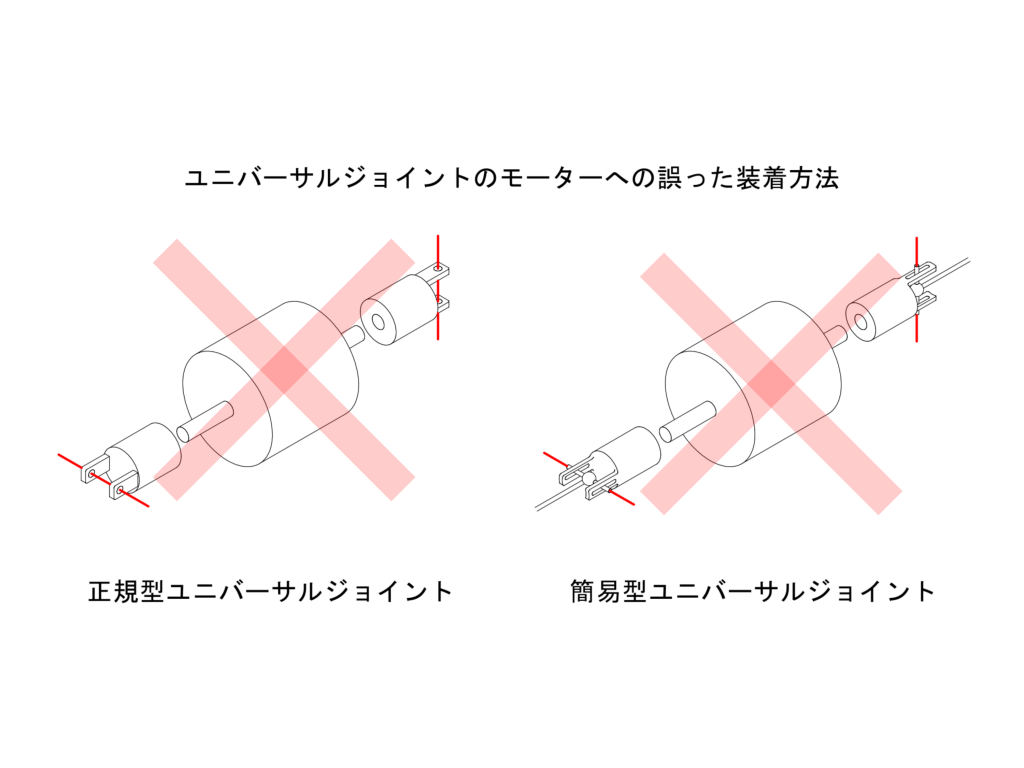
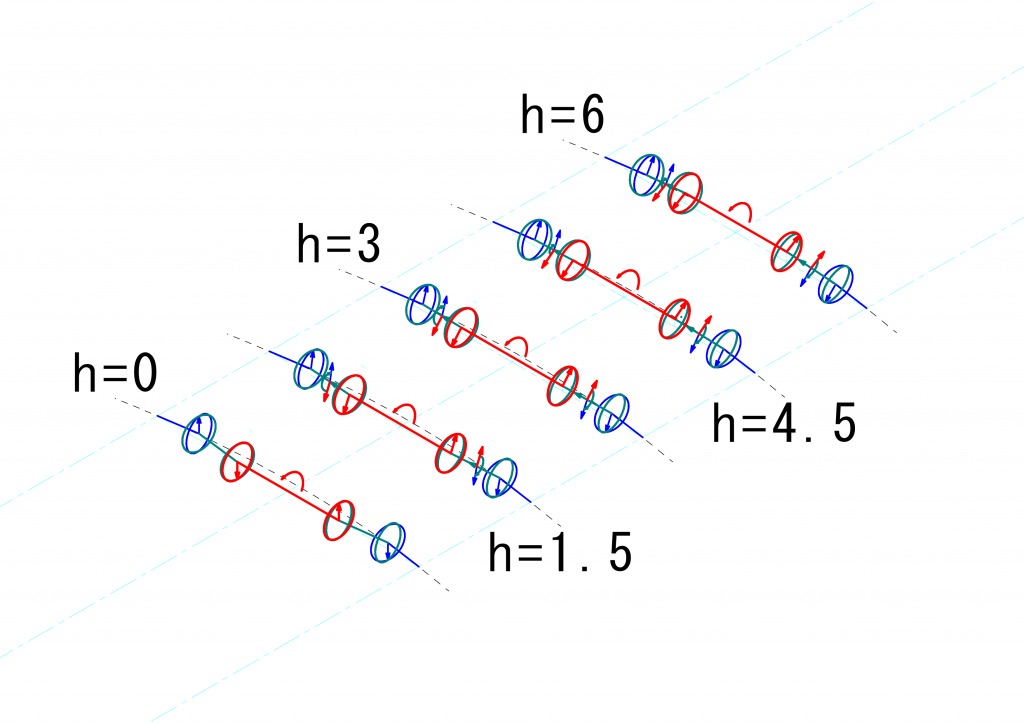
2020/8/30追記。 Tavataさんにいただいたコメントを参考に追記しました。

前回説明した2つのベクトルのなす角度および外積を利用し、3つの軸が同一平面上にないユニバーサルジョイントの解析に必要となる\(\alpha\)、\(\beta\)、\(\eta\)の計算方法を考察してゆきます。

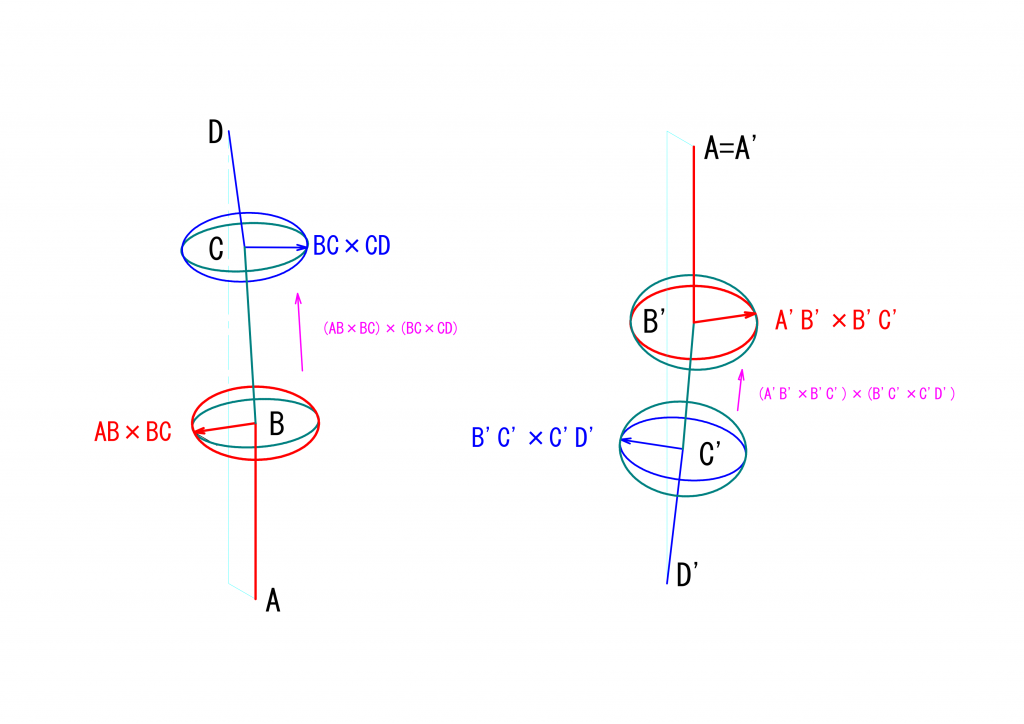
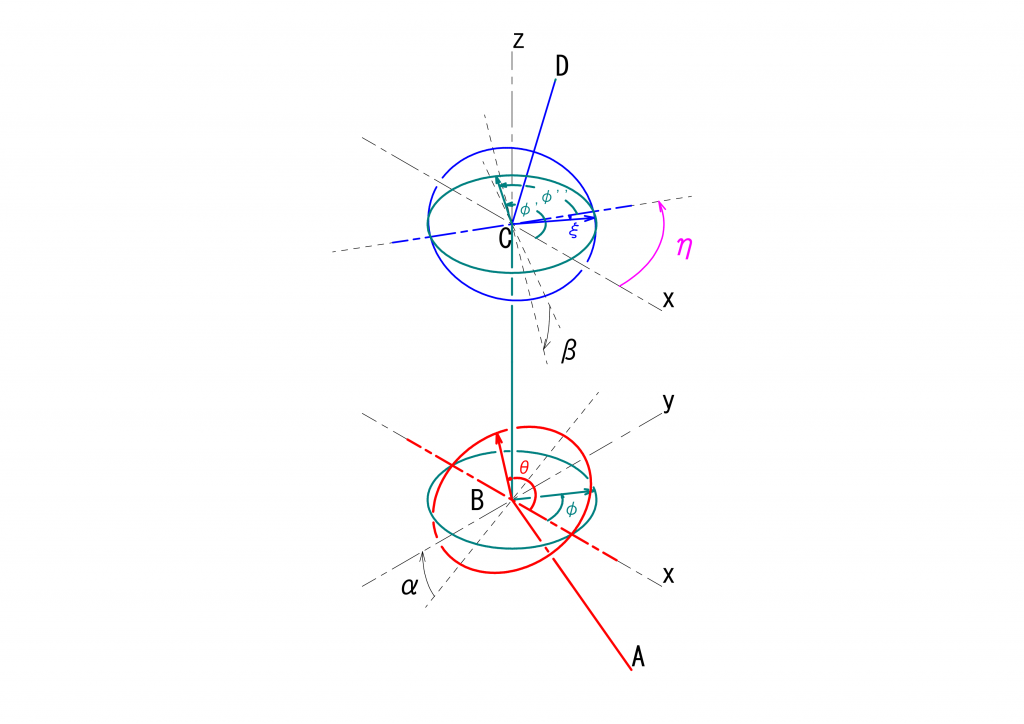
以前示した図ですが、ユニバーサルジョイントは3つの軸で構成され、4つの点\(A\)、\(B\)、\(C\)、\(D\)で規定されます。軸\(AB\)が軸\(BC\)に動力を伝え、軸\(BC\)が軸\(CD\)に動力を伝えるものとします。

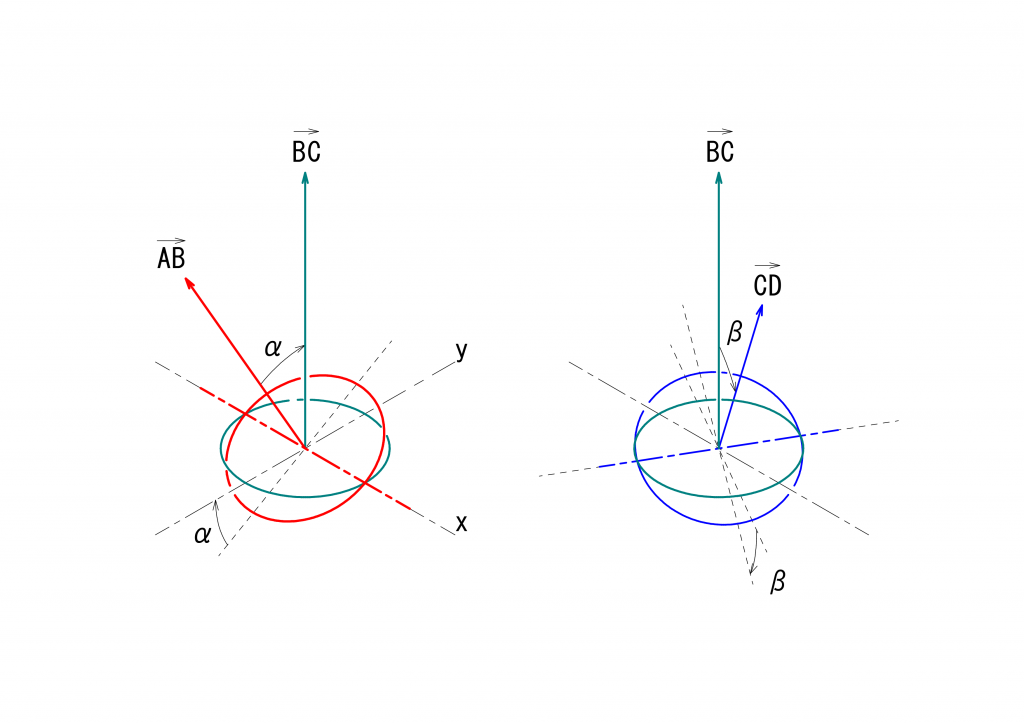
このとき、\(B\)を通り\(AB\)に垂直な赤い円を含む平面が駆動面、\(B\)を通り\(BC\)に垂直な緑の円を含む平面が伝達面、となります。駆動面に対する伝達面の傾き\(\alpha\)は、ベクトル\(\vec{AB}\)とベクトル\(\vec{BC}\)とのなす角度として求めることができます。

\(cos(\alpha)=\frac{\vec{AB}\cdot\vec{BC}}{|\vec{AB}|\cdot|\vec{BC}|}\)

同じ議論が中継面と最終伝達面に関しても成り立ちます。\(C\)を通り\(BC\)に垂直な緑の円を含む平面が中継面、\(C\)を通り\(CD\)に垂直な青い円を含む平面が最終伝達面、となります。ベクトル\(\vec{BC}\)とベクトル\(\vec{CD}\)とのなす角度が中継面に対する最終伝達面の傾き\(\beta\)となります。

\(cos(\beta)=\frac{\vec{BC}\cdot\vec{CD}}{|\vec{BC}|\cdot|\vec{CD}|}\)

これらの4つのベクトルと、\(\alpha\)、\(\beta\)の関係を念のために次に示します。

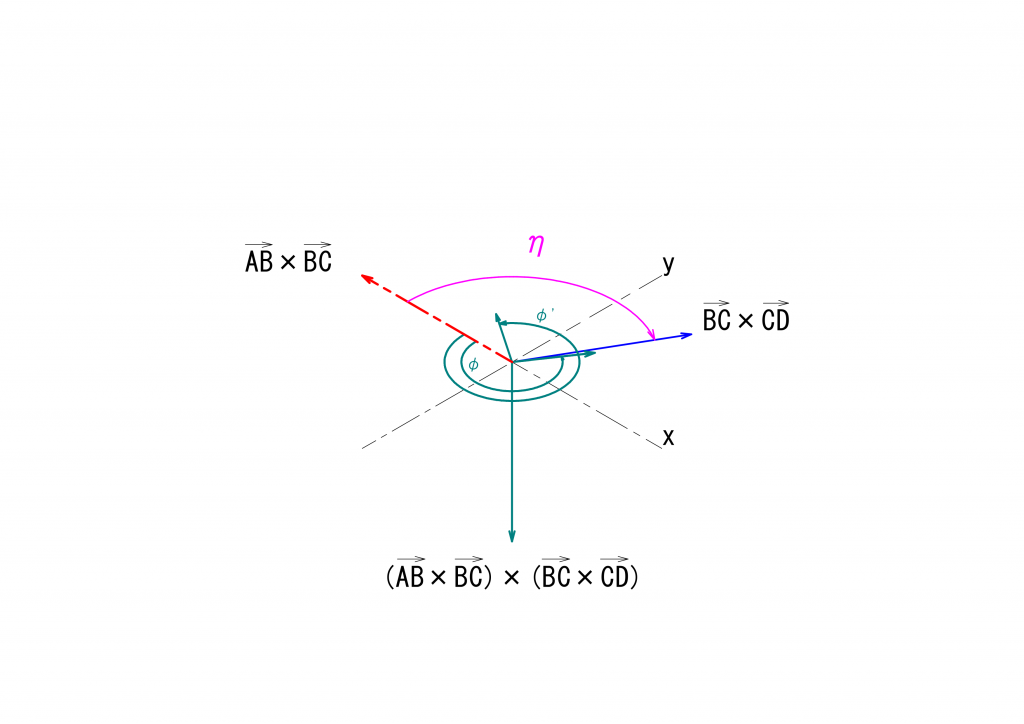
次に\(\eta\)を求めます。これは、駆動面および伝達面を回転する点の回転角の基準となる線（赤の一点鎖線）に対して、中継面と最終伝達面を回転する点の回転角の基準となる線（青の一点鎖線）がどれだけ回転しているかを表す角度です。

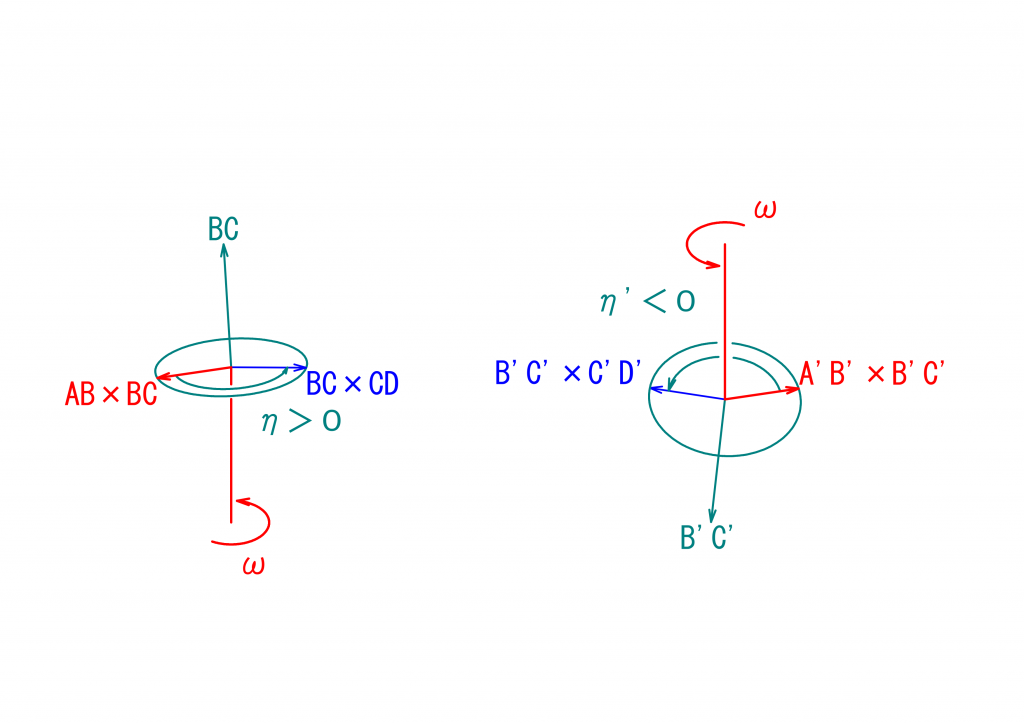
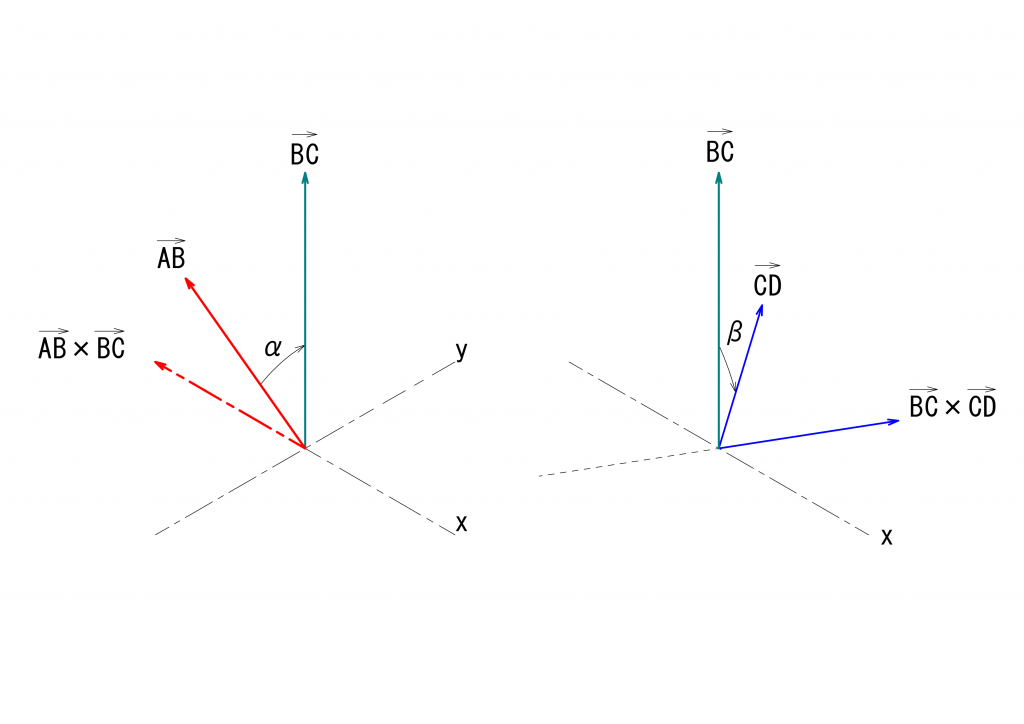
駆動面および伝達面を回転する点の回転角の基準となる線は\(AB\)および\(BC\)に垂直であることを思い出せば、\(\vec{AB}\)と\(\vec{BC}\)の外積\(\vec{AB}\times\vec{BC}\)を基準線として利用することができます。同様に、中継面と最終伝達面を回転する点の回転角の基準となる線として、\(\vec{BC}\)と\(\vec{CD}\)との外積\(\vec{BC}\times\vec{CD}\)を利用することができます。

これらの関係を下の図に示します。なお、今回の議論ではベクトルの外積の向きにだけ興味がありますので、ベクトルの大きさは必ずしも正しくありません。

\(\eta\)を求めるには、\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta_{abs}\)を求め、\(\vec{AB}\times\vec{BA}\)に対する\(\vec{BC}\times\vec{CD}\)の回転方向に応じて符号を与えることが必要です。

まず、\(\eta_{abs}\)は次の式を使って求める事ができます。

\(cos(\eta_{abs})=\frac{(\vec{AB}\times\vec{BC})\cdot(\vec{BC}\times\vec{CD})}{|\vec{AB}\times\vec{BC}|\cdot|\vec{BC}\times\vec{CD}|}\)

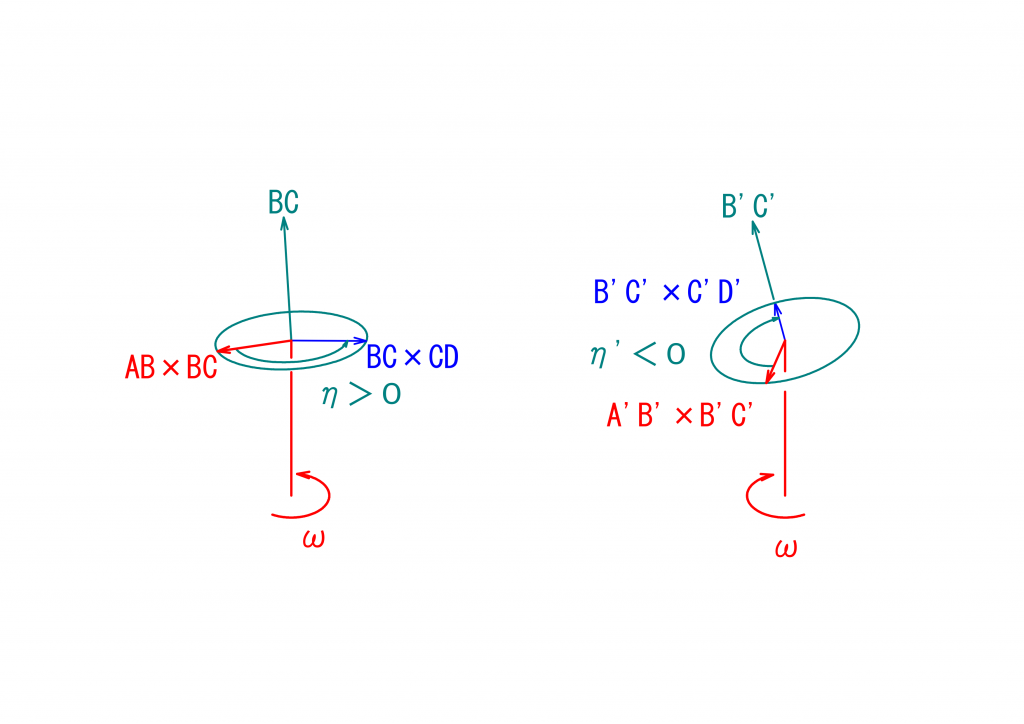
\(BC\)と垂直な２つのベクトル\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)の外積ベクトル\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)を求めると、\(\vec{BC}\)か\(\vec{CB}\)かのいずれかと同じ向きを向くベクトルとなります。

\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)と\(\vec{BC}\)との内積が、正、負に応じて、\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)はそれぞれ、\(\vec{BC}\)、\(\vec{CB}\)と同じ向きとなります。

\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)が\(\vec{BC}\)と同じ方向の場合、\(\vec{BC}\)の方向にネジを締める向きに\(\vec{AB}\times\vec{BA}\)を回転すれば、\(\vec{BC}\times\vec{CD}\)と同じ向きとなりますので、\(\eta=\eta_{abs}\)とします。さもなくば、\(\eta=-\eta_{abs}\)とします。

2つのベクトルが同じ向きかを調べる方法はいくつか考えられますが、ここでは以下の方法をとります。

2つのベクトルが同じ向き（反対向き）の場合は、2つのベクトルのなす角は\(0\)（\(\pi\))となり、そのなす角の余弦(\(cos\))は1(-1)となります。2つのベクトルの内積を、2つのベクトルの長さの積で割ったものは、2つのベクトルのなす角の余弦(\(cos\))となることを思い出せば、

\(\eta=\eta_{abs}\cdot\frac{((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD}))\cdot\vec{BC}}{|(\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})|\cdot|\vec{BC}|}\)

となります。

最初に示した図の場合では、\((\vec{AB}\times\vec{BA})\times(\vec{BC}\times\vec{CD})\)は\(\vec{CB}\)と同じ向きを向きますので、\(\vec{AB}\times\vec{BA}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta_{abs}\)に\(-1\)をかけたものが\(\eta\)となります。

これを図示したのが下となります。この時、中継面の基準点の角度\(\varphi’\)と最終伝達面の基準点の角度\(\xi\)との間の関係式は、次のようになります。

\(tan(\xi) = -\frac{1}{tan(\varphi’-(-\eta))}\cdot\frac{1}{cos(\beta)}\)

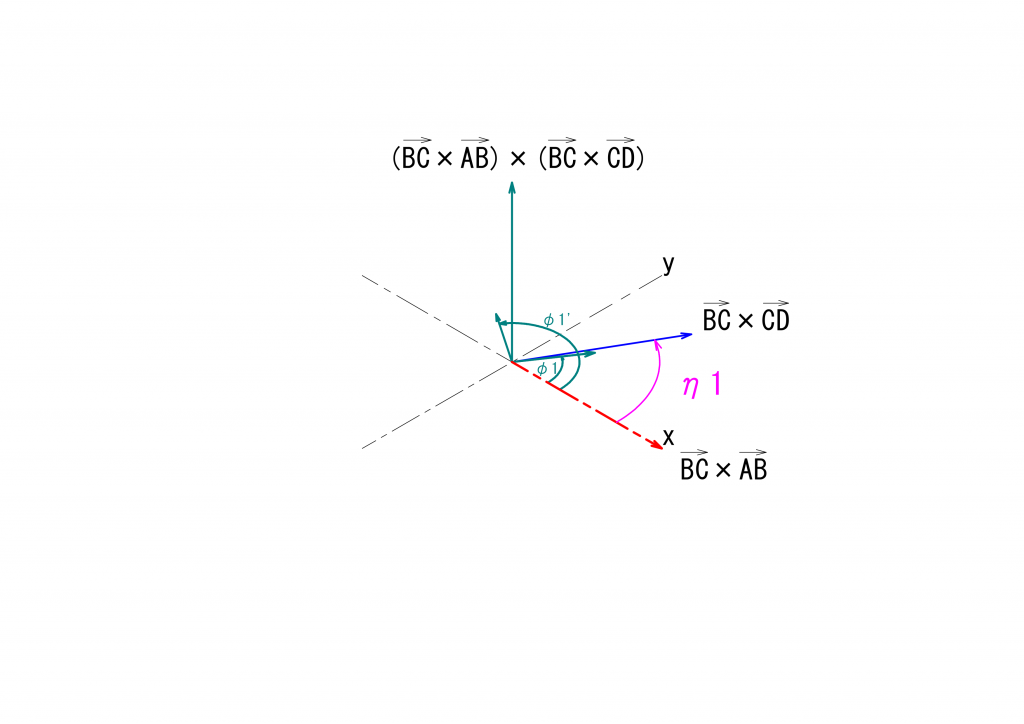
最初に示した図からは、次のような図を連想するかと思いますが、上の図とは随分と様子が異なります。これはどういうことでしょうか。

この図では、中継面の基準点の角度\({\varphi_1}’\)と最終伝達面の基準点の角度\(\xi\)との間には次の関係が成り立ちます。

\(tan(\xi) = -\frac{1}{tan({\varphi_1}’-\eta_1)}\cdot\frac{1}{cos(\beta)}\)

\({\varphi_1}’=\varphi’-\pi\)、\(\eta_1=\pi-\eta\)ですので、これを上の式に代入すると、

\(tan(\xi) = -\frac{1}{tan(\varphi’-2\pi-\eta)}\cdot\frac{1}{cos(\beta)}\)

となります。三角関数の周期性から\(tan(\theta-\pi) = tan(\theta)\)ですので、この式は

\(tan(\xi) = -\frac{1}{tan(\varphi’-\eta)}\cdot\frac{1}{cos(\beta)}\)

となり、先ほど図の説明で示した式そのものです。つまり、上の2つの図は見た目は異なりますが、実は全く同じ計算をしていることになります。

あるいは直感的には、\(\vec{BC}\times\vec{CD}\)を起点に、反時計回りに\(\eta\)と\(\varphi’\)の角度の和の\(tan\)を求めるわけですが、これが一回り以上していますので、その一回り分の\(2\pi\)を差し引くというのが、\(tan(\varphi’-\eta-2\pi)\)という式に表れてくる、と考えることもできます。

ユニバーサルジョイントの3つの軸が同一平面にある場合は、作図によって、わかりやすい方向を人間が考えて式をたてることができました。3つの軸が同一平面にない場合は、ここで説明したようなベクトルの演算で解析を行いました。ベクトルの向きを厳密にしかし一貫性のあるように、扱うことになったと言えます。

---

念のため今までの議論による計算方法を示します。これまでの議論をもとに、計算に集中できるようにした式ですので、冗長な記述となっている点をご了解ください。

まず、\(A\)、\(B\)、\(C\)、\(D\)の座標をそれぞれ\(A=(a_x,a_y,a_z)\)、\(B=(b_x,b_y,b_z)\)、\(C=(c_x,c_y,c_z)\)、\(D=(d_x,d_y,d_z)\)とします。原点をどのように設定しても結果は変わりませんので、考えやすい点を原点として座標を決めれば大丈夫です。

すると、

\(\vec{AB}=(b_x-a_x, b_y-a_y, b_z-a_z)\)

\(\vec{BC}=(c_x-b_x, c_y-b_y, c_z-b_z)\)

\(\vec{CD}=(d_x-c_x, d_y-c_y, d_z-c_z)\)

となります。式が複雑になるので、以下

\(\vec{AB}=(b_x-a_x, b_y-a_y, b_z-a_z)=(ab_x, ab_y,ab_z)\)

\(\vec{BC}=(c_x-b_x, c_y-b_y, c_z-b_z)=(bc_x,bc_y,bc_z)\)

\(\vec{CD}=(d_x-c_x, c_y-c_y, d_z-c_z)=(cd_x,cd_y,cd_z)\)

と置きます。

\(\alpha\)、\(\beta\)はこれらから

\(\alpha=cos^{-1}(\frac{ab_x\cdot bc_x+ab_y\cdot bc_y+ab_z\cdot bc_z}{\sqrt{{ab_x}^2+ {ab_y}^2+ {ab_z}^2}\cdot\sqrt{{bc_x}^2+ {bc_y}^2+ {bc_z}^2}})\)

\( \beta=cos^{-1}(\frac{bc_x\cdot cd_x+bc_y\cdot cd_y+bc_z\cdot cd_z}{\sqrt{{bc_x}^2+ {bc_y}^2+ {bc_z}^2}\cdot\sqrt{{cd_x}^2+ {cd_y}^2+ {cd_z}^2}})\)

と求めることができます。

次に、\(\vec{AB}\)と\(\vec{BC}\)との外積、\(\vec{BC}\)と\(\vec{CD}\)との外積、を求めます。

\(\vec{AB}\times\vec{BC} = (ab_y\cdot bc_z-ab_z\cdot bc_y, ab_z\cdot bc_x-ab_x\cdot bc_z, ab_x\cdot bc_y-ab_y\cdot bc_x)\)

\(\vec{BC}\times\vec{CD} = (bc_y\cdot cd_z-bc_z\cdot cd_y, bc_z\cdot cd_x-bc_x\cdot cd_z, bc_x\cdot cd_y-bc_y\cdot cd_x)\)

式が複雑にならないよう、

\(\vec{AB}\times\vec{BC} = (ab_y\cdot bc_z-ab_z\cdot bc_y, ab_z\cdot bc_x-ab_x\cdot bc_z, ab_x\cdot bc_y-ab_y\cdot bc_x)\)

\(=(abc_x,abc_y,abc_z)\)

\(\vec{BC}\times\vec{CD} = (bc_y\cdot cd_z-bc_z\cdot cd_y, bc_z\cdot cd_x-bc_x\cdot cd_z, bc_x\cdot cd_y-bc_y\cdot cd_x)\)

\(=(bcd_x,bcd_y,bcd_z)\)

と置きます。

すると、\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)とのなす角\(\eta\)の絶対値は、

\(|\eta| = cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)

となります。

\(\vec{AB}\times\vec{BC}\)と\(\vec{BC}\times\vec{CD}\)との外積は、次のように計算できます。

\((\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD}) = \)

\((abc_y\cdot bcd_z-abc_z\cdot bcd_y, abc_z\cdot bcd_x-abc_x\cdot bcd_z, abc_x\cdot bcd_y-abc_y\cdot bcd_x)\)

\(\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD})\)と\(\vec{BC}\)との内積を計算します。

\((\vec{AB}\times\vec{BC})\times(\vec{BC}\times\vec{CD})\cdot\vec{BC}=\)

\(((abc_y\cdot bcd_z-abc_z\cdot bcd_y)\cdot bc_x,(abc_z\cdot bcd_x-abc_x\cdot bcd_z)\cdot bc_y, (abc_x\cdot bcd_y-abc_y\cdot bcd_x)\cdot bc_z)\)

先ほどはこの値を２つのベクトルの長さの積で割り、2つのベクトルの余弦を求めましたが、数値計算の誤差が出る場合があるので、上の値の符号で判定する方が現実的かと思います。

従って、上記の内積が正であれば、

\(\eta=cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)

上記の内積が負であれば、

\(\eta=-cos^{-1}(\frac{abc_x\cdot bcd_x+abc_y\cdot bcd_y+abc_z\cdot bcd_z}{\sqrt{{abc_x}^2+ {abc_y}^2+ {abc_z}^2}\cdot\sqrt{{bcd_x}^2+ {bcd_y}^2+ {bcd_z}^2}})\)

となります。

次回は、この結果を使って実際の数値を当てはめる予定です。