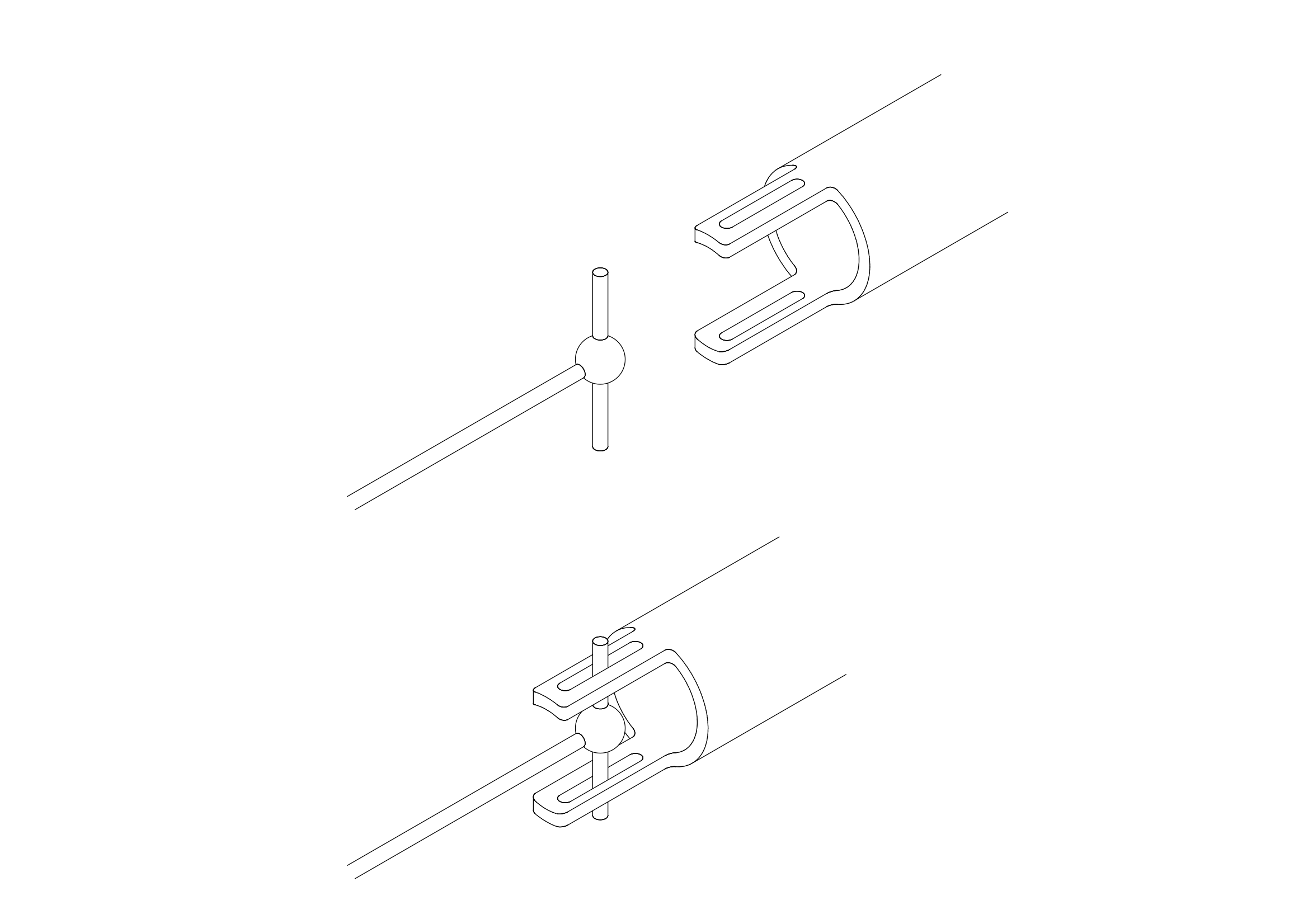
これまで議論してきたユニバーサルジョイントとは異なり、模型では下図のように構成を簡素化したユニバーサルジョイントが使われることが多くあります。ここでは、これまで議論してきたものを正規型ユニバーサルジョイントと、簡素化したものを簡易型ユニバサールジョイントと呼ぶこととします。簡易型ユニバーサルジョイントについても、正規型ユニバーサルジョイントについて述べたことがそのまま成立するのか、見てみたいと思います。
以後の議論では、簡易型ユニバーサルジョイントの各部の名称を次のようにします。正式名称もしくはより一般的に使われる名称をご存じの方は、お知らせください。まず、下図の右側の動力源につなぐ、もしくは最終的に動力を伝達する部品で、上下2本伸びて円筒を切り欠いた部分を「爪」、そこに開いている長細い穴を「ガイド」、下図左側の部品でガイドにはまる部分を「ピン」、ピンに直交し動力を伝達する軸を「伝達軸」と呼ぶこととします。
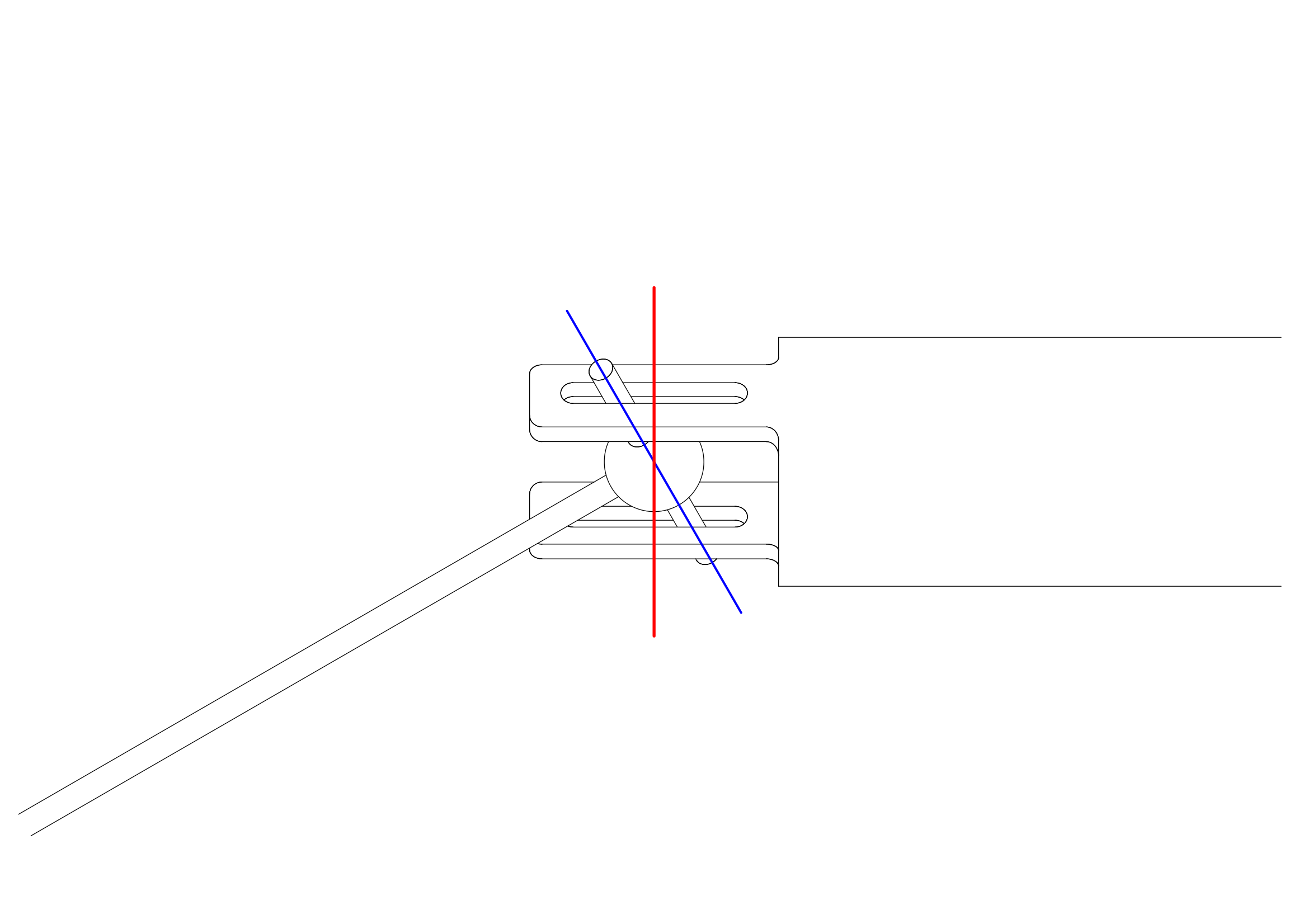
簡易型ユニバーサルジョイントが回転する様子を下図に示します。ピンの中心は、青い線で示す平面上を移動します。ガイドの中心は、赤い線で示される平面上を移動します。実際には、ピンの位置がガイドに沿って移動する余地があるのではありますが、ここではピンの中心とガイドの中心とが交わる点は動かないという理想的な状態を仮定して議論を進めます。
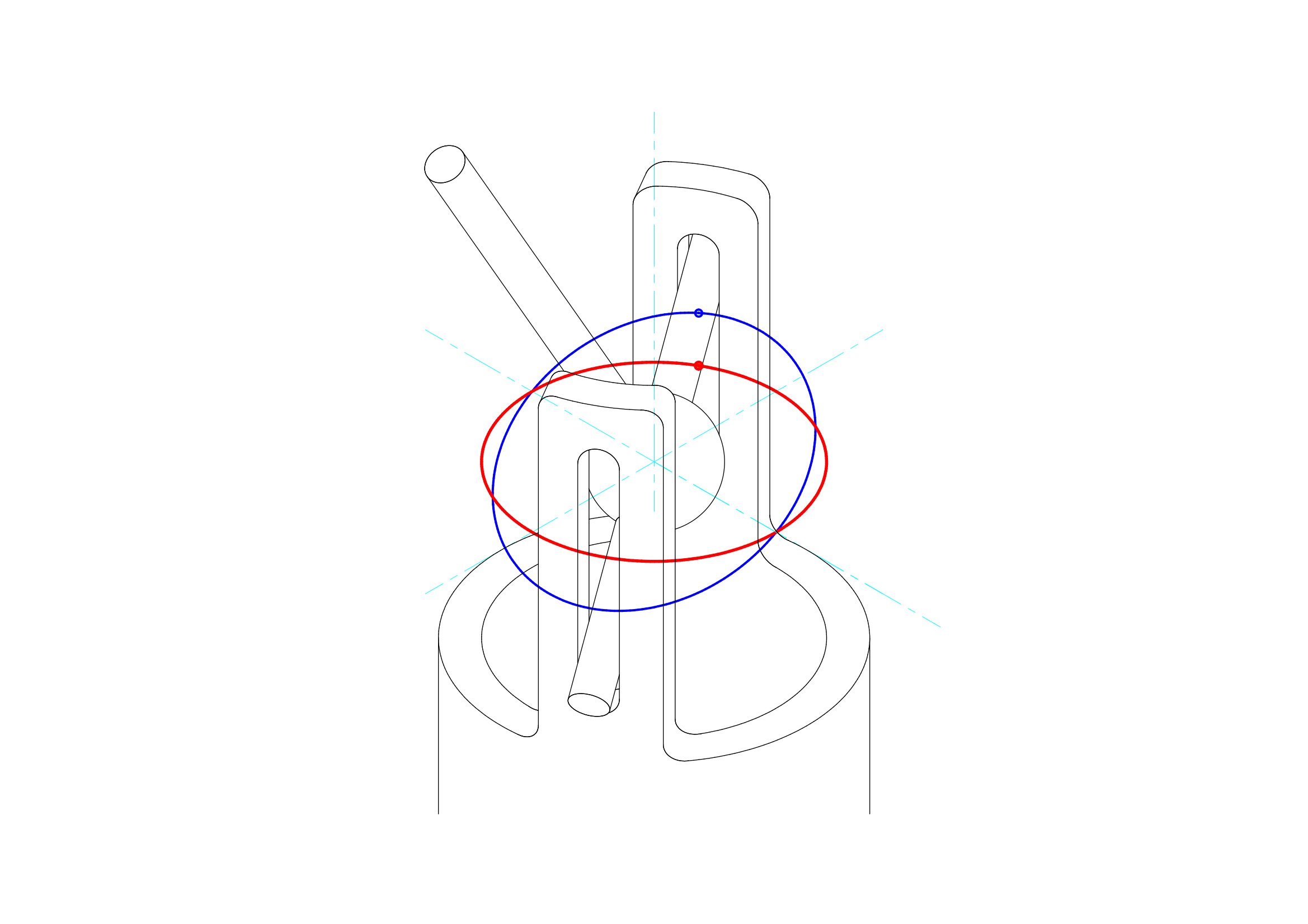
上で述べたピンの中心とガイドの中心を立体的に見たのが次の図です。ピンと駆動軸の中心が交わるところを原点し、ガイドの中心位置の基準点(赤い点)が赤で示した水平面上の円形の軌道を移動するものとします。この時、赤い点を通る\(z\)軸方向の垂直な線と、ピンの中心軸とが交わった基準点(青い点)は、水平面に対して傾いた青で示した楕円形の軌道を移動します。なお、ガイドの中心位置の正確な位置については、下図では爪の内側の円筒面にあるものとして作図しましたが、赤の基準点と青の基準点とがz軸方向の垂直線上にある限り、爪の外側の円筒面でも、爪の厚みの中心でも構いません。
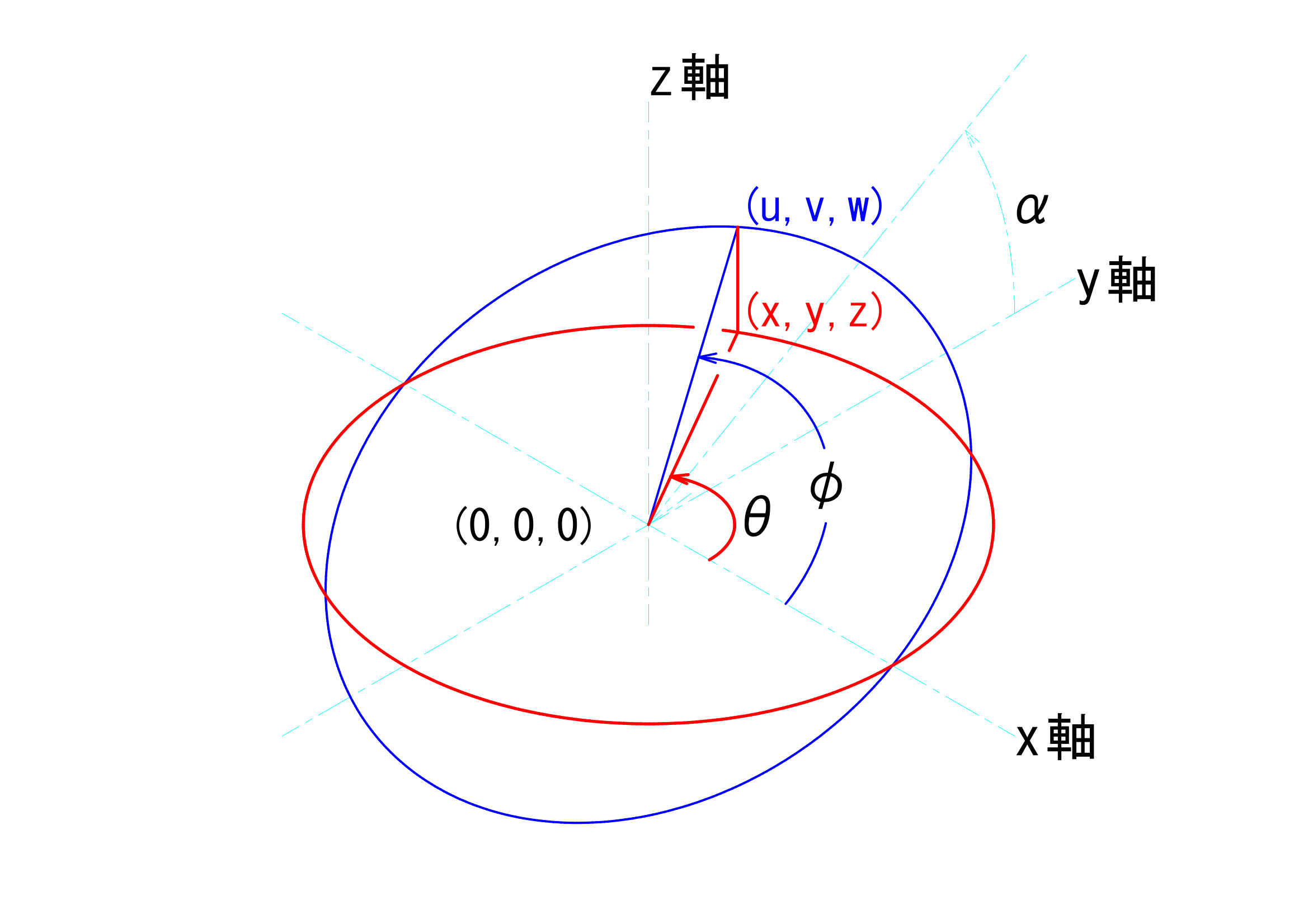
赤の点の座標を\((x,y,z)\)、青の点の座標を\((u,v,w)\)とします。原点\((0,0,0)\)と\((x,y,z)\)の距離を\(r\)としたときに、これらの2点を結ぶ直線が水平面上で\(x\)軸となす角度を\(\theta\)とします。また、原点\((0,0,0)\)と\((u,v,w)\)との距離を\(l\)とし、これらの2点を結ぶ直線が水平面に対して\(\alpha\)傾いた面で\(x\)軸となす角を\(\varphi\)とします。これを示したのが下図です。
この時、
\((x,y,z) = (r\cdot cos(\theta), r\cdot sin(\theta), 0)\)
\((u,v,w) = (l\cdot cos(\varphi), l\cdot sin(\varphi)\cdot cos(\alpha), l\cdot sin(\varphi)\cdot sin(\alpha))\)
が成立します。
\((u,v,w)\)、\((x,y,z)\)は、垂直線上に位置しますので、\(u = x\)、\(v = y\)が成立します。したがって、
\(r\cdot cos(\theta) = l\cdot cos(\varphi)\)
\(r\cdot sin(\theta) = l\cdot sin(\varphi)\cdot cos(\alpha))\)
という2つの式を得ることができます。下の式の左辺を上の式の左辺で、下の式の右辺を下の式の右辺で割ると、
\(\frac{r\cdot sin(\theta)}{r\cdot cos(\theta)} = \frac{l\cdot sin(\varphi)\cdot cos(\alpha)}{l\cdot cos(\varphi)}\)
となります。\(\frac{sin(\theta)}{cos(\theta)}=tan(\theta)\)でしたので、上記の式は
\(tan(\theta) = tan(\varphi)\cdot cos(\alpha)\)
と整理できます。従って、正規型ユニバーサルジョイントで得られた式に似た
\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)
という関係を得ることができます。\(\varphi\)については、
\(\varphi = tan^{-1}(tan(\theta)\cdot\frac{1}{cos(\alpha)})\)
と計算することができます。
ここでの議論では必要ありませんでしたが、参考までに原点\((0,0,0)\)と\((u,v,w)\)との距離\(l\)を計算してみます。先ほどの2つの式について、左辺の二乗の和と、右辺の二乗の和は等しいので、
\(r^2\cdot sin^2(\theta) + r^2\cdot cos^2(\theta) = l^2\cdot cos^2(\varphi) + l^2\cdot sin^2(\varphi)\cdot cos^2(\alpha)\)
を得ます。\(sin^2(\theta)+cos^2(\theta)=1\)ですので、この式は
\(r^2=l^2(cos^2(\varphi)+sin^2(\varphi)\cdot cos^2(\alpha))\)
と変形できます。右辺の括弧の中は、
\(cos^2(\varphi) + sin^2(\varphi)\cdot cos^2(\alpha)\)
\(=cos^2(\varphi) + sin^2(\varphi)\cdot cos^2(\alpha) + sin^2(\varphi)\cdot sin^2(\alpha) – sin^2(\varphi)\cdot sin^2(\alpha)\)
\(=cos^2(\varphi) + sin^2(\varphi)\cdot (cos^2(\alpha) + sin^2(\alpha)) – sin^2(\varphi)\cdot sin^2(\alpha)\)
\(=cos^2(\varphi) + sin^2(\varphi) – sin^2(\varphi)\cdot sin^2(\alpha)\)
\(=1- sin^2(\varphi)\cdot sin^2(\alpha)\)
と整理することができます。
これをもとの式に代入し、
\(r^2=l^2(1-sin^2(\varphi)\cdot sin^2(\alpha))\)
を得、最終的に
\(l = \frac{r}{\sqrt{1- sin^2(\varphi)\cdot sin^2(\alpha)}}\)
\(= \frac{r}{\sqrt{1- sin^2( tan^{-1}(tan(\theta)\cdot\frac{1}{cos(\alpha)}))\cdot sin^2(\alpha)}}\)
を得ます。