大学の一般教養課程で、「図学」を学びました。3次元空間の物体の幾何学的な関係についての問題を2次元の紙の上に表現して解く、と言えばよいのでしょうか。白状すると、「とりあえず単位はもらいました」程度の成績だったのですが、その理由の一つは「解こうとしている問題の諸条件を的確に盛り込んだ図をフリーハンドで描く」ということが不得手である、ということだと思っています。

そういえば、フリーハンドで円を描くのが抜群に上手い物理の先生が高校にいました。数学とか物理とかが得意な人は、こういった図を的確に描く能力もあるのではないか、などということを思ったものでした。

そういう私にとって、CADツールは、図面を描く道具だけでなく、ウン十年前の鬱憤を晴らすというと大げさですが、図学的思考をする道具としても重宝しています。今回のユニバーサルジョイントの件も、頭を整理するのにずいぶんと役立ちました。

ということで、これまで式で表現してきたユニバーサルジョイントの基準点の関係を図で表現したものを載せておきます。dda40xさんの紹介されたT氏のようなエレガントな図にはできませんが、まぁ、こういう見方もある、程度で参考になれば幸いです。

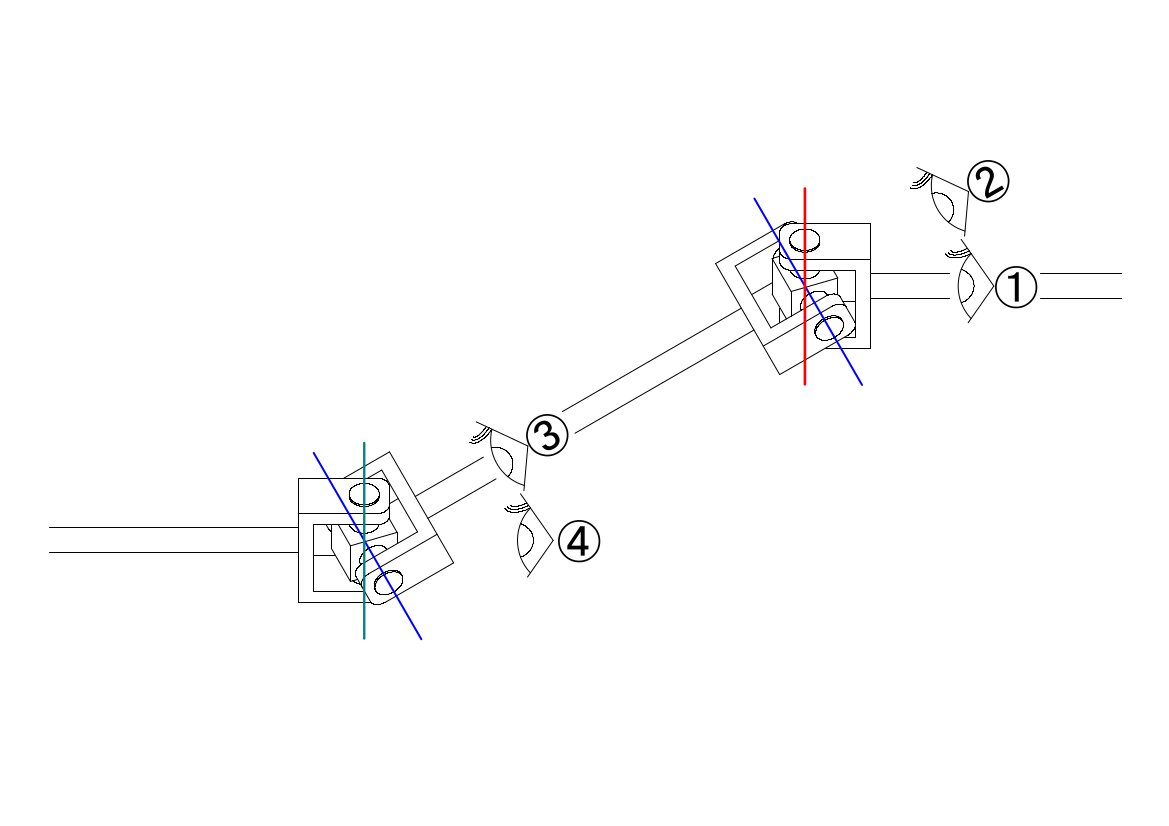
下は、ジョイントを同位相にした場合の図です。①は駆動面を、②は伝達面を、③は中継面を、④は最終伝達面を、それぞれ正面から見た様子を示します。なお、駆動面と伝達面とがなす角度と、中継面と最終伝達面とがなす角度は（絶対値が）同じであるとします。

それぞれの位置でどのように見えるかを示したのが下の図です。

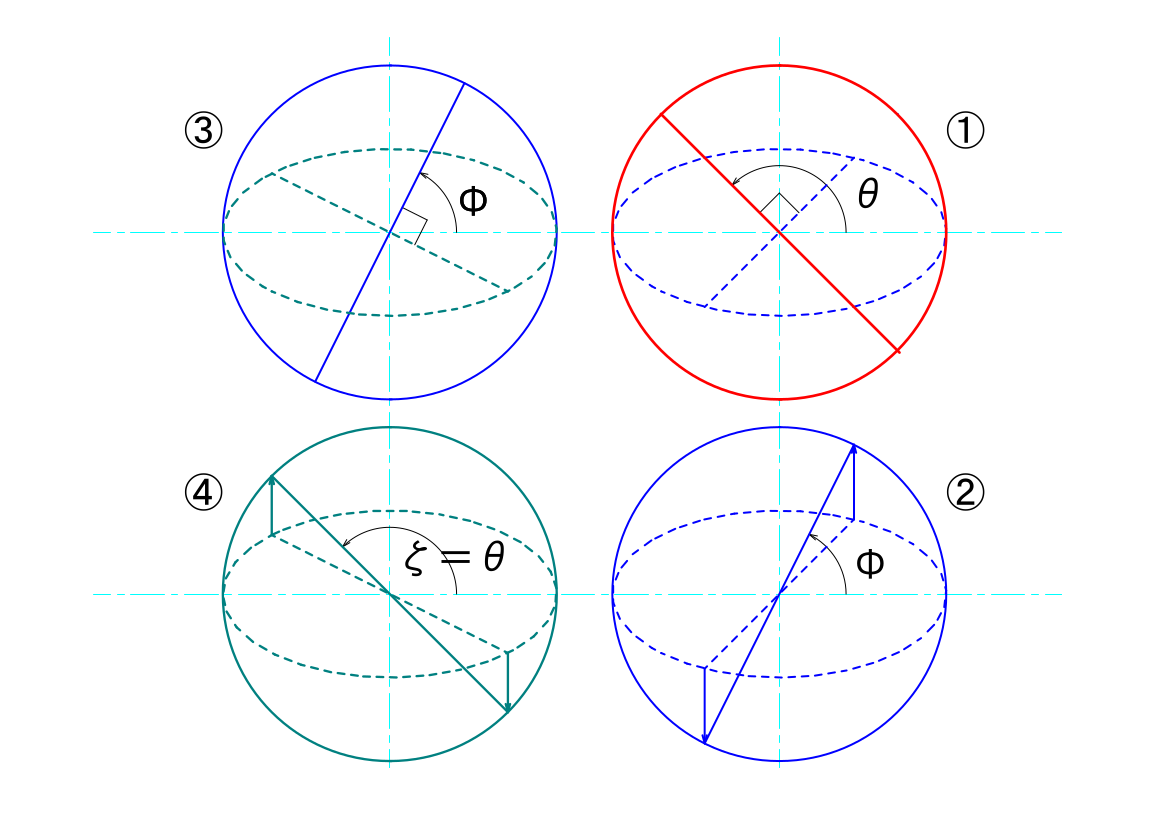
駆動面①の基準点は、半径\(r\)の赤い線上を移動し、\(\theta\) の角度にあるとします（赤い線）。また、伝達面②は、①の視点からは青い点線の楕円に見えます。この楕円の高さは、基準点の回転半径を\(r\)、駆動面に対する伝達面の傾きを\(\alpha\)としたとき、\(r\cdot cos(\alpha)\)となります。このとき、伝達面の基準点は青い点線の楕円を移動し、この楕円と\(\theta\)に直交した青い点線とが交わったところに位置します。

伝達面の視点で見たのが②です。①で見えた楕円の上の基準点は、この点から\(y\)軸方向に延ばした線と、青い実線の円と交差するところとなります。これが先に示した、

\(tan(\varphi) = tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\)

の式の意味するところです。実際にCADツールで作図して\(\varphi\)を計測してみると、上記の式で計算した値が得られます。

中継面の視点で見たのが③です。伝達面と中継面とは同位相ですから、中継面の基準点は、青い実線上ので\(\varphi\)の角度に位置します。中継面に直交する最終伝達面の基準点は\(\varphi\)に直交した角度で、緑の点線の楕円の上を動きます。

最終伝達面の視点で見たのが④です。これは①と②との関係と同じで作図すればよく、緑の点線の楕円上の点から\(y\)軸方向に延ばした線と緑の実線の円と交差する点に基準点が位置します。図から赤い実線と緑の実践とが平行であることがわかると思いますが、実際にCADツールで計測しても\(\xi=\theta\)であることがわかります。

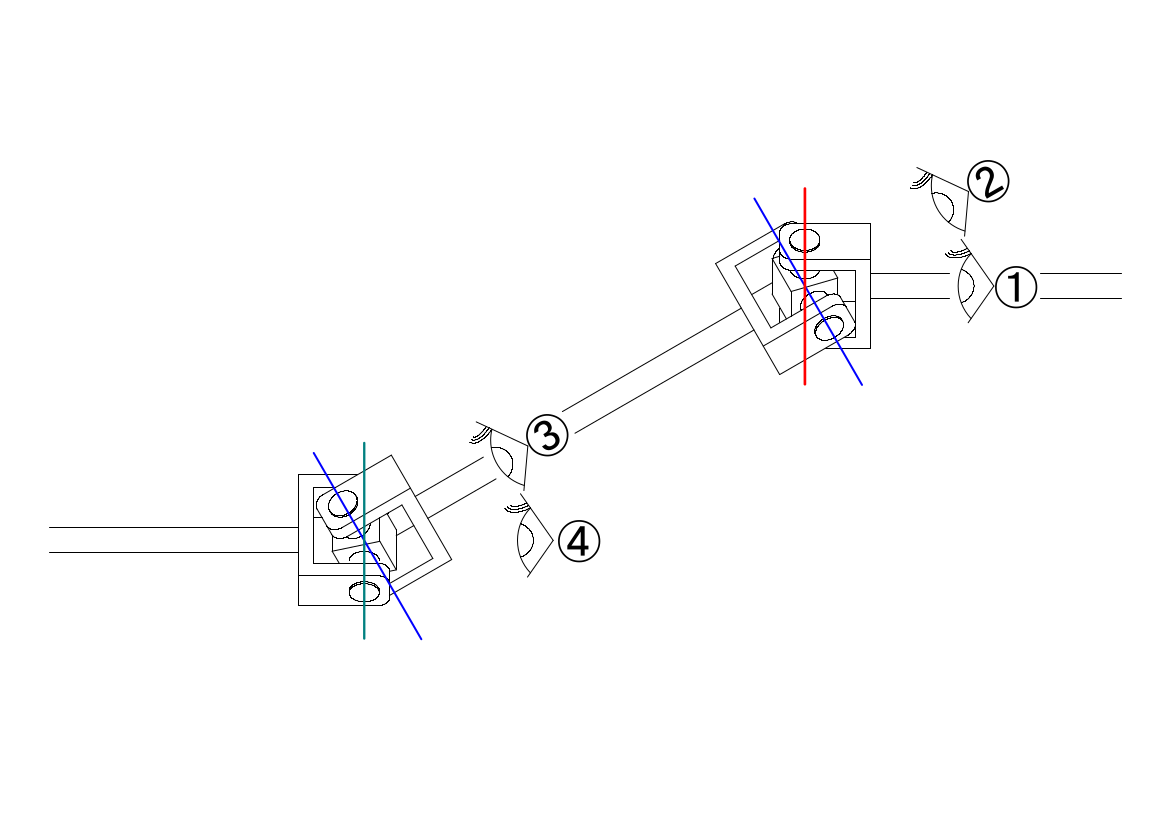
次は、伝達面②と中継面③との基準点を９０度(\(\frac{\pi}{2}\))ずらした場合を考えます。

この場合、駆動面①、伝達面②、中継面③、最終伝達面④を正面から見るとどうなるか、というのが下の図です。今回も、駆動面と伝達面とがなす角度と、中継面と最終伝達面とがなす角度は（絶対値が）同じであるとします。

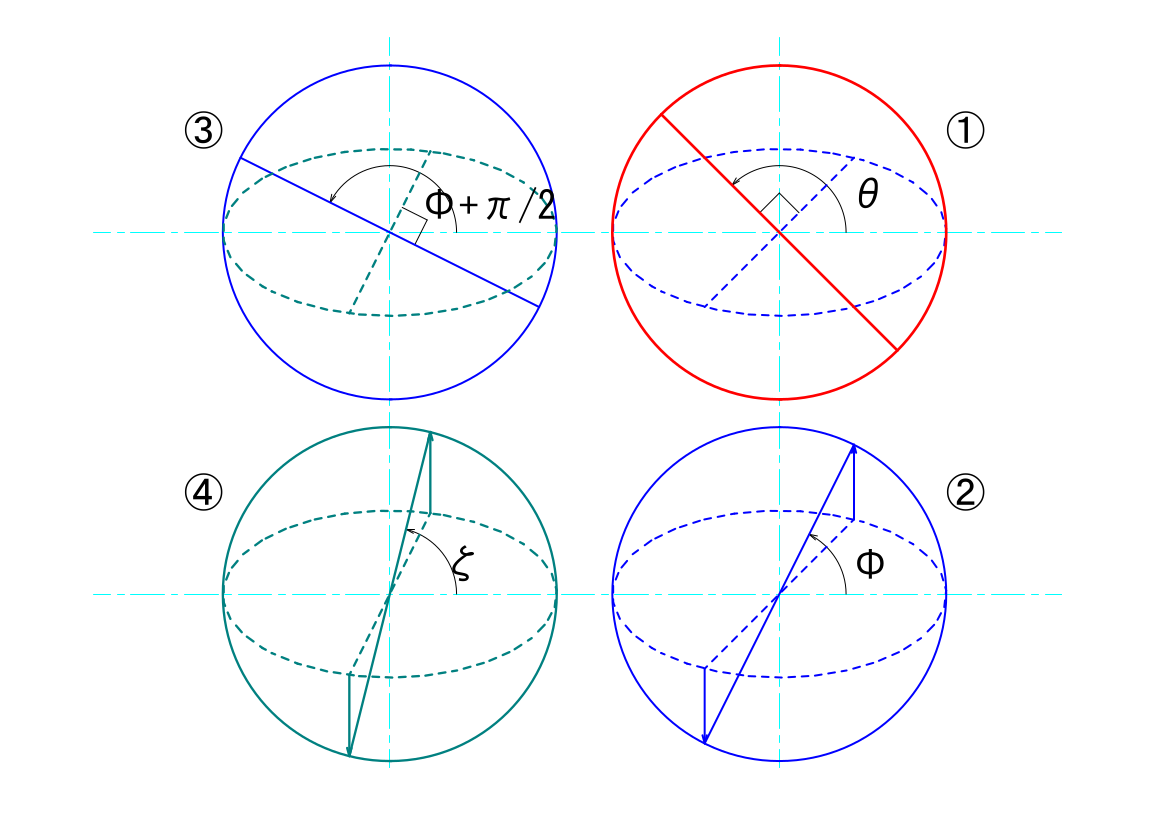
まず、①、②の図は前回と全く同じとなります。③の中継面の基準点は②の伝達面の基準点に直交しますのでその角度は異なりますが、③、④で作図する方法は前回と同じ考え方です。

もともとの期待は、最終伝達面④の基準点の角度\(\xi\)が、伝達面①の基準点の角度\(\theta\)に対して９０度異なる角度にあるということですが、この図は、そうはならない、ということを示しています。

②と④とを見ていただければわかりますが、②で\(\theta-\frac{\pi}{2}\)に対して\(\varphi\)は角度が進み、④でさらに\(\xi\)で角度が進む、ということがわかります。これが、前回導出した

\(tan(\xi) = tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

の式の意味するところです。