次に、２つのユニバーサルジョイントを組み合わせる事を考えます。

まず、前回の議論で、駆動面に対し伝達面が\(\alpha\)だけ傾いている場合、駆動面を回転する基準点の\(x\)軸に対する角度\({\theta}\)と、伝達面を回転する基準点の\(x\)軸に対する角度\({\varphi}\)とには、次の関係が成立することを示しました。

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\alpha)}\)

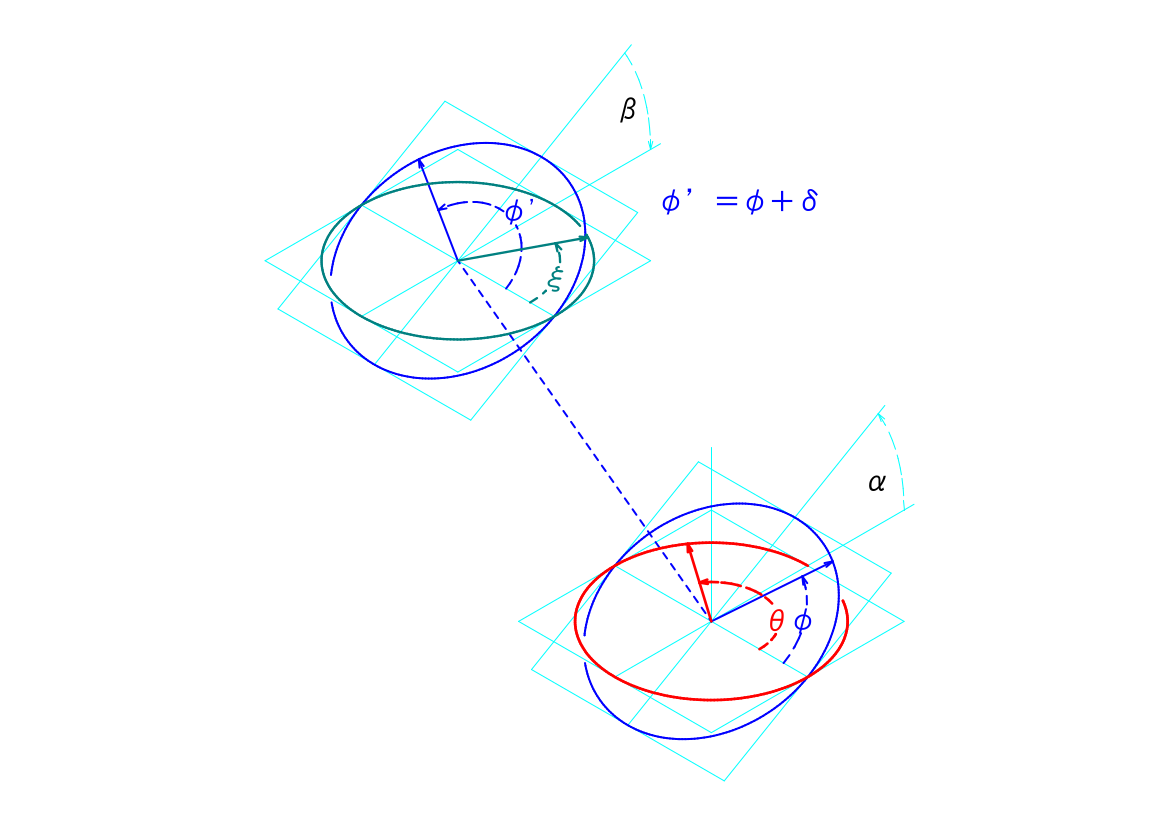
この伝達面の先に、もう一つのジョイントをつなげることを考えます。下図にこの様子を示します。

図の下にある赤の円が駆動面で、青の円が伝達面を示します。それぞれの基準点の角度が\(\theta\)、\(\varphi\)となります。

もう一つのジョイントの十字型部品の基準点の移動する円を２つ、図の上の方に青の円と緑の円とで示します。ここでは、青の円を中継面、緑の円を最終伝達面、と呼ぶこととします。なお、議論を簡単にするために、ここでは駆動面につながっている軸、伝達面と中継面をつなぐ軸、最終伝達面につながっている軸、の３つは、同一平面上にあるものとします。

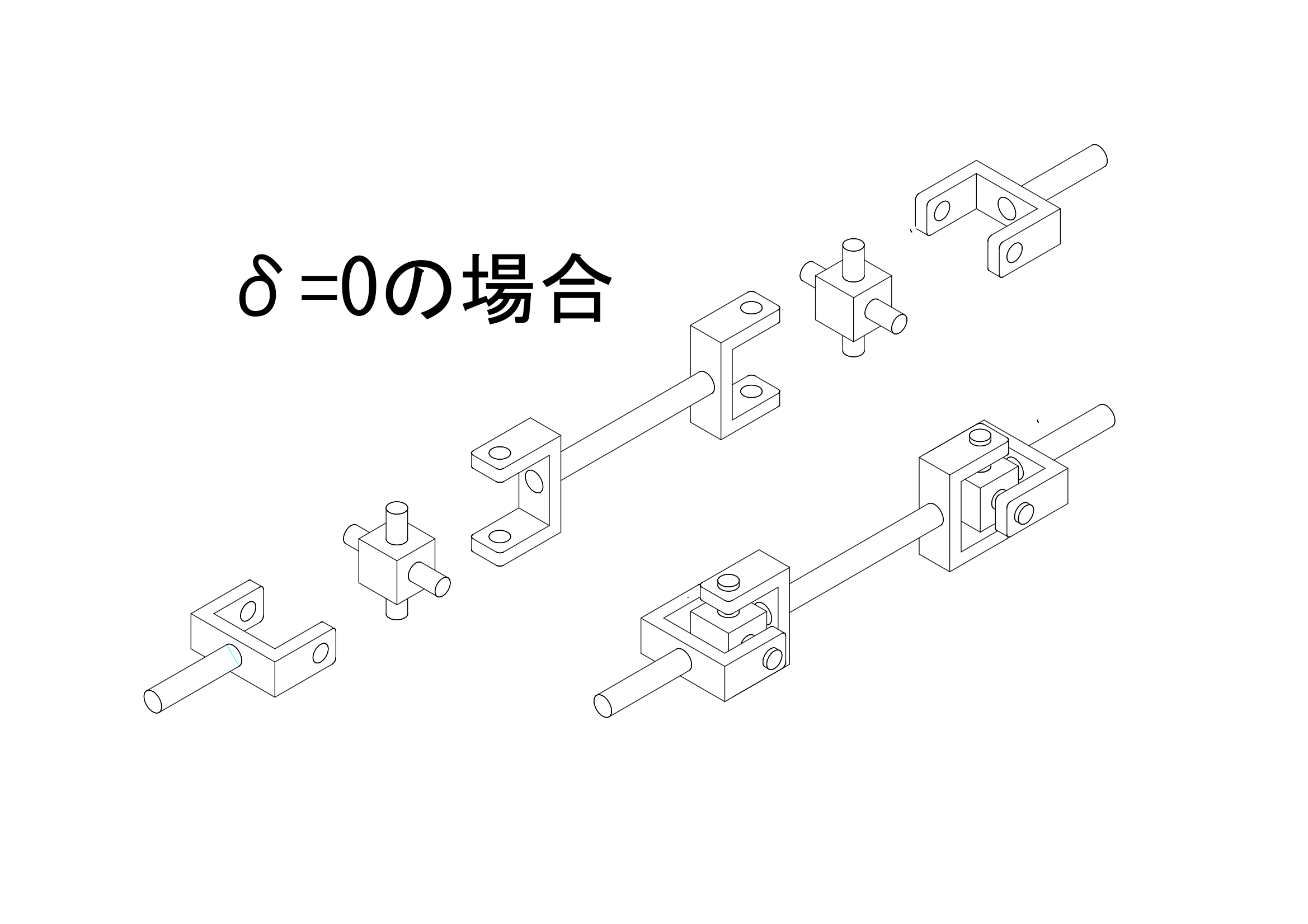
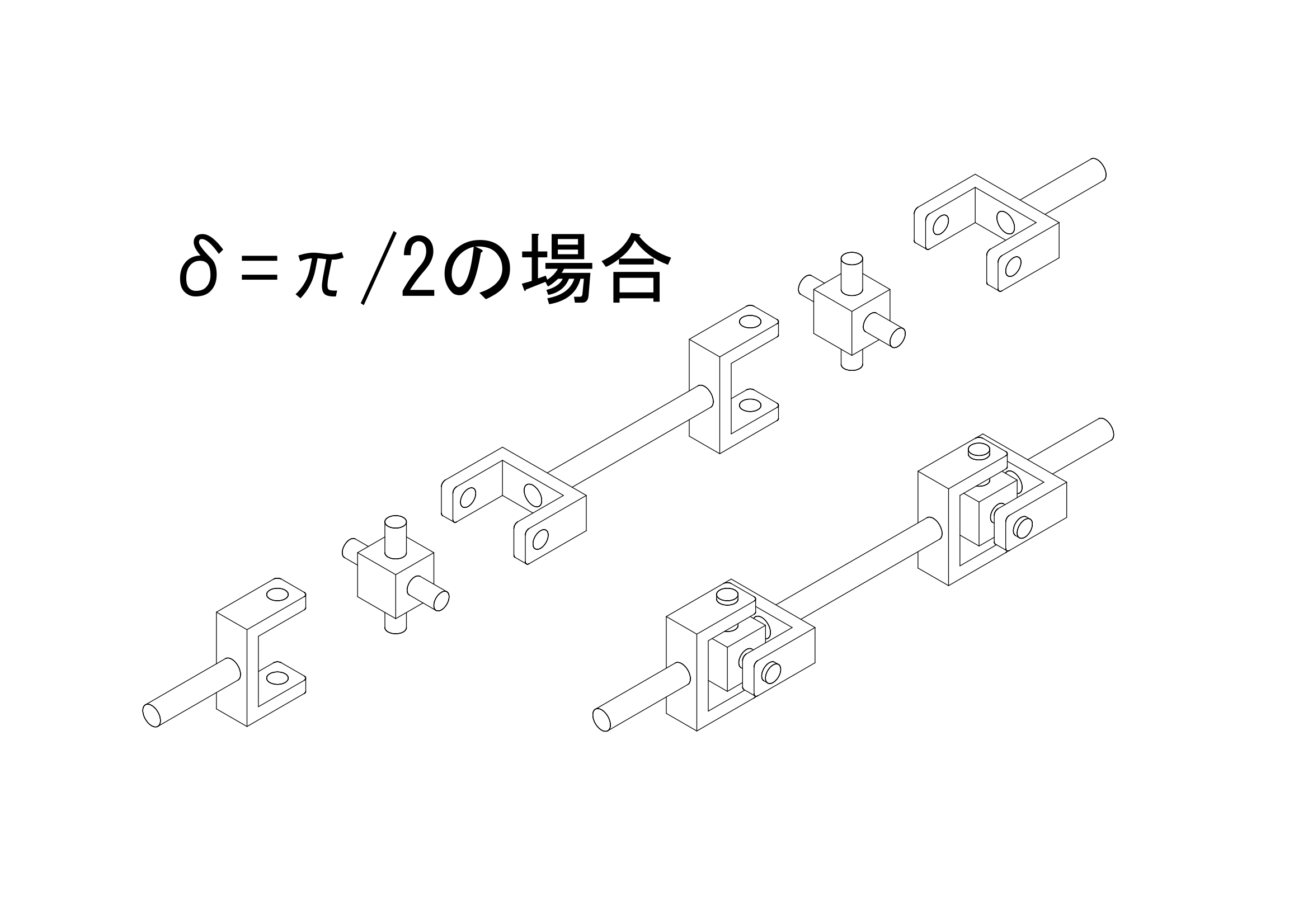
中継面は伝達面と平行であり、その中継面上を移動する基準点の角度を\(\varphi\prime\)とし、伝達面の基準点の角度\(\varphi\)に対して、\(\varphi\prime=\varphi+\delta\)という関係が成り立つものとします。つまり\(\delta=0\)であれば、ジョイントは同位相で、\(\delta=\frac{\pi}{2}\)であれば、ジョイントは90度ひねられて取り付けられていることとなります。

また、最終伝達面は、中継面に対して\(\beta\)傾いているものとし、最終伝達面の基準点の角度を\(\xi\)とします。

さて、中継面の基準点の角度\(\varphi\prime\)と最終伝達面の基準点の角\(\xi\)との関係は、\(\theta\)と\(\varphi\)との関係と同じで、次の式が成り立ちます。

\(tan(\xi)=-\frac{1}{tan(\varphi^\prime)}\cdot\frac{1}{cos(\beta)}\)

\(\varphi^\prime=\varphi+\delta\)でしたので、上記の式は、

\(tan(\xi)=-\frac{1}{tan(\varphi+\delta)}\cdot\frac{1}{cos(\beta)}\)

となります。

上記の式の中の\(tan(\varphi+\delta)\)に注目します。2つの角度の和のタンジェントは次のように書き変えることができます。

\(tan(\varphi+\delta)=\frac{tan(\varphi)+tan(\delta)}{1-tan(\varphi)\cdot tan(\delta)}\)

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\)を代入すると、

\(tan(\varphi+\delta)\) = \(\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+tan(\delta)}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot tan(\delta)}\)

となり、\(tan(\delta)=\frac{sin(\delta)}{cos(\delta)}\)であったことを思い出し、分子と分母とに\(tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)\)をかけると、

\(tan(\varphi+\delta)=\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+\frac{sin(\delta)}{cos(\delta)}}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot \frac{sin(\delta)}{cos(\delta)}}=\frac{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}\)

これを、最初の式に代入すると

\(tan(\xi)=-\frac{1}{tan(\theta+\delta)}\cdot \frac{1}{cos(\beta)}=-\frac{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

となり、少し見やすく整理すると、

\(tan(\xi)=\frac{sin(\delta)+tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta)-tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

という式が得られます。

さて、いつも議論となるのは、ジョイントが同位相か、\(\frac{\pi}{2}\)（90度）ひれらているかです。

上の図のように、ジョイントを同位相とするということは、\(\delta=0\)とするということですので、\(sin(0)=0\)、\(cos(0)=1\)となります。これを代入すると

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}\)

となります。従って、\(\alpha=\beta\)であれば、

\(tan(\xi)=tan(\theta)\)

となります。

この式は、ジョイントを同位相にし、2つのジョイントの傾きを同じにしておけば、一方のジョイントの不等速性は、もう一方のジョイントで打ち消され、駆動面と、最終伝達面との位相とは、同じであり、等速性が保証される、ということとなります。

また、\(cos(\theta)=cos(-\theta)\)であったことを思い出すと、上記の式は、

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(\alpha)}{cos(-\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(-\beta)}\)

のいずれでも成立することがわかります。つまり、上で述べたジョイントの2つの傾きが同じ、というのは、傾きの絶対値が同じと言い換えてよいことがわかります。

上の図のように、ジョイントを90度回転させると、\(\delta=\frac{\pi}{2}\)となりますので、\(sin(\frac{\pi}{2})=1\)、\(cos(\frac{\pi}{2})=0\)を先ほどの式に代入すると、

\(tan(\xi)=-\frac{1}{tan(\theta)\cdot cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、少し変形すると、

\(tan(\xi)=tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、ユニバーサルジョイント1個の時によく似た形の式となります。異なるのは、\(\frac{1}{cos(\beta)}\)が付け加わっていることです。

ユニバーサルジョイント1個の時は、駆動面の基準点の角度に比して、伝達面面の基準点の角度が進む、ということでしたが、ユニバーサルジョイント2個の際は、さらにもう一回角度が進むこととなり、つまりは、不等速性を増大させる、ということがわかります。

（この項続く）