随分と間が空いてしまいました。きわめて忙しかったこともあるのですが、この2回後に書きたいと思っている内容をうまくまとめることできず、考え込んでいたのもあります。もう忘れ去られているかもしれませんが、これまでの議論の続きを行います。

前回は\(|\alpha|=|\beta|\)となるような \(\alpha\)と\(\beta\)との関係を考えました。端的に言うと、\(|\alpha|=|\beta|\)となるような機構を模型において実現するのは容易ではなく、\(|\alpha|\ne|\beta|\)となる状況が発生することを念頭に置かなければならない、ということです。

今回は模型で一般的に使われると思われる機構において、\(\alpha\)と\(\beta\)とが、どのような関係となるかを考察してみたいと思います。下記は、dda40xさんのblogで紹介された機構です(商品名は、エンドウのMPギア)。なお、写真はdda40xさんのblogから拝借しています。

この機構では、カーブでの台車の回転に伴って左側のC点が回転し、右側のC点との間が伸び縮みします。

以下の議論を進めるために、この機構を持った車両が円弧上を走行している状態を下図のようにモデル化します。二本の線路の中心の円弧を紫の点線が、上の写真の左側のC点から車体の端より（左側）に位置するモーターからの駆動力を車輪に伝える軸を青い実線が表します。赤の実線は上の写真の右側のC点から車体中央寄りののC点から車体中心より（右側）のモーターの軸を表し、これは車体に対して固定されています。緑の実線が2つのC点の間をつなぐBのパーツに相当し、カーブ走行時に伸縮します。

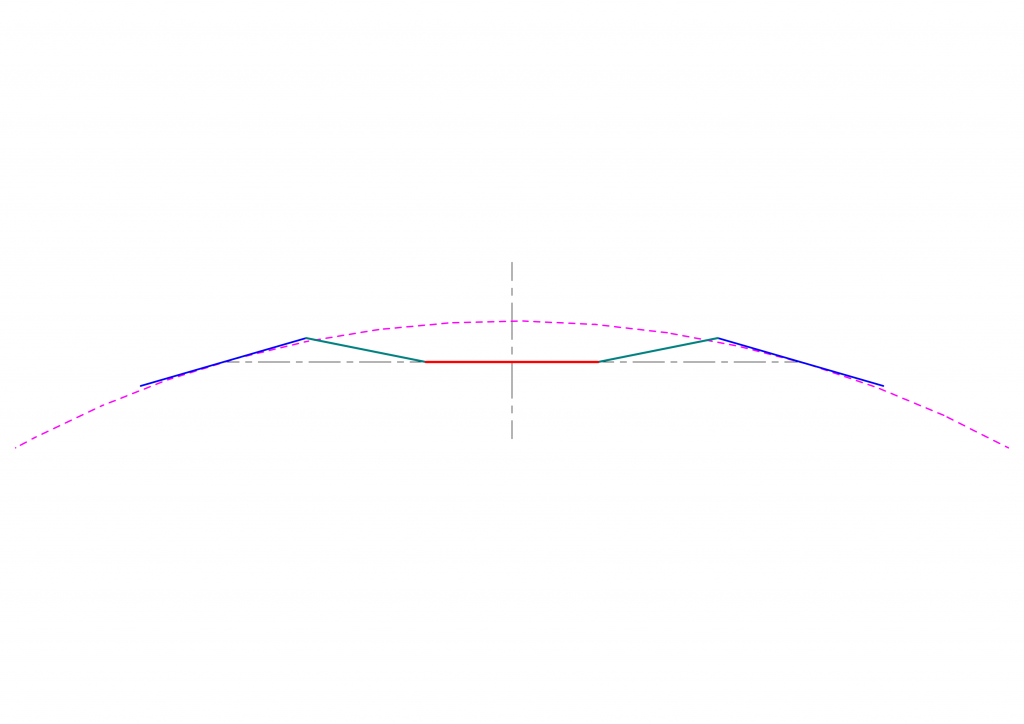
これらの位置関係を数式で表してゆきます。まず、走行中の曲線の半径を\(r\)とします。\(o\)は車体の中心の位置を、\(c_1\)、\(c_2\)は台車の中心の位置を表します。\(a_1\)、\(a_2\)は、モーター側のユニバーサルジョイントの中心の位置を、\(b_1\)、\(b_2\)は、台車側のユニバーサルジョイント中心の位置を示します。\(c_1\)、\(a_1\)、\(o\)、\(a_2\)、\(c_2\)を通る直線に対して、\(b_1\)、\(b_2\)から 垂直に線を引いたときにこの直線と交わる点をそれぞれ\(d_1\)、\(d_2\)とします。

\(c_1\)と\(c_2\)の距離、つまり線分\(c_1c_2\)の長さ、を\(2\cdot w\)とします。\(o\)は\(c_1c_2\)の中心となりますので、線分\(oc_1\)の長さは、\(w\)となります。線分\(oa_1\)の長さを\(l_1\)、線分\(b_1c_1\)の長さを\(l_2\)とします。

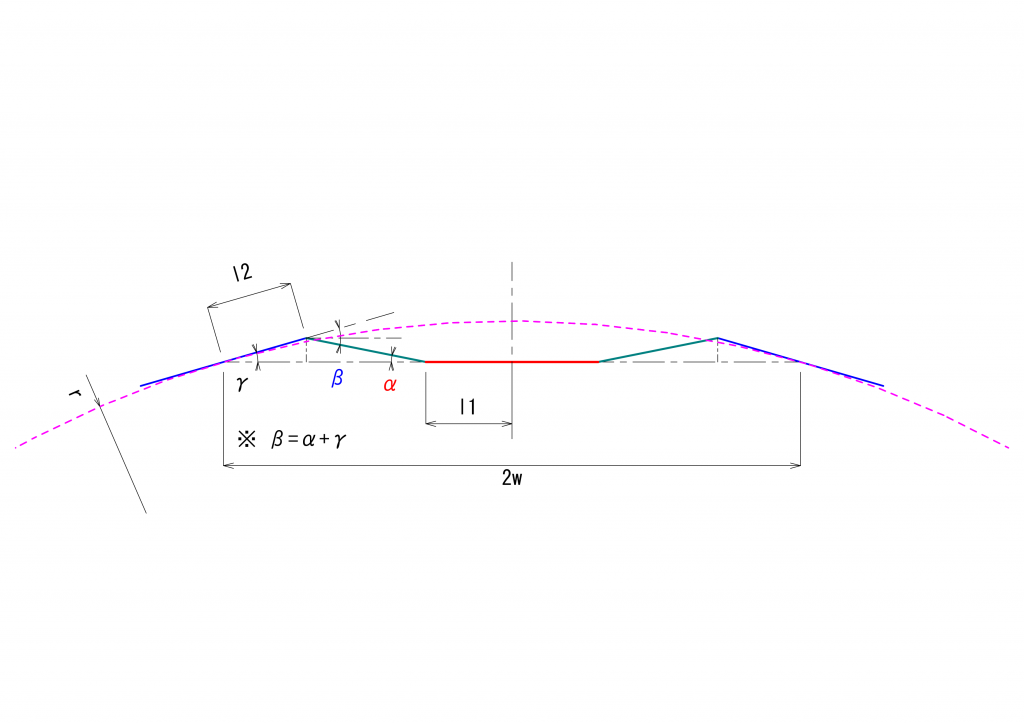
実際に台車が曲線でどれだけ回転するかを厳密に求めるのは簡単ではないと思いますので、\(b_1c_1\) は、半径\(r\)の曲線に\(c_1\)において接するという仮定を置きます。言い換えると、\(c_1\)は半径\(r\)の円の上にある点であり、かつ、\(c_1\)とこの円との中心\(O_r\)（注：上の図には示していません）とを結んだ線は \(b_1c_1\) と直交します。

また、\(a_1d_1\)と\(a_1b_1\)のなす角度を\(\alpha\)、\(c_1b_1\)を車体中心方向（右）に延長した線と\(b_1a_1\)とのなす角度を\(\beta\)、\(c_1d_1\)と\(c_1b_1\)のなす角度を\(\gamma\)、とします。

半径\(r\)の円弧の中心\(O_r\)と\(c_1\)、\(c_2\)とがなす三角形は、二等辺三角形となり、その底角は\(\frac{\pi}{2}-\gamma\)となります。また、底辺の\(c_1c_2\)の長さは\(2\cdot w\)、等辺\(O_rc_1\)、\(O_rc_2\)の長さは\(r\)となりますので、三角関数の定義から、

\(\frac{w}{r}=cos(\frac{\pi}{2}-\gamma)\)

が成立します。

\(b_1\)、\(c_1\)、 \(d_1\) がなす直角三角形に注目すると、線分\(c_1d_1\)の長さは\(l_2\cdot cos(\gamma)\)、線分\(b_1d_1\)の長さは\(l_2\cdot sin(\gamma)\)、であることが三角関数の定義から導けます。

\(b_1\)、\(d_1\)、\(a_1\)がなす直角三角形に注目します。線分\(a_1d_1\)の長さは、線分\(oc_1\)の長さから、上で求めた線分\(c_1d_1\)の長さ\(l_2\cdot cos(\gamma)\)と、線分\(oa_1\)の長さである\(l_1\)を引いた、\(w-l_1-l_2\cdot cos(\gamma)\)となります。線分\(b_1d_1\)の長さは上で求めた\(l_2\cdot sin(\gamma)\)でしたので、

\(tan(\alpha) = \frac{l_2\cdot sin(\gamma)}{w – l_2\cdot cos(\gamma) – l_1}\)

が成立します。

また、２つの平行な線に交わる線を引いたときの錯角、同位角の関係から、\(b_1\)を起点に\(c_1o\)に平行な補助線を引くと、\(\beta = \alpha + \gamma\)が成立することがわかります。

これまでの議論をまとめると\(\alpha\)、\(\beta\)を求めるには、

\(\gamma = \frac{\pi}{2}-{cos}^{-1}(\frac{w}{r})\)

\(\alpha = {tan}^{-1}(\frac{l_2\cdot sin(\gamma)}{w – l_2\cdot cos(\gamma) – l_1})\)

\(\beta = \alpha + \gamma\)

を順に計算すればよいことがわかります。

この式から確認できることは、MPギアでは、曲線に入ると、\(|\alpha|\ne|\beta|\)という状況が発生する、つまり、台車を駆動する側の軸では、角速度の変動が必ず発生する、ということです。

次回は実際にいくつかの数値を当てはめて考察を進めます。