このシリーズを延々続けているのは、Shayのユニバーサルジョイントの角速度の変化を解析したかったからでした。ということで、Shayの場合の\(\alpha\)と\(\beta\)とを求めてみます。
求め方はMPギアの場合に準じますが、MPギアの駆動軸が車体の中心に位置するのに対し、Shayの駆動軸は車体の中心からオフセットしていることを考慮に入れる必要があります。更に、駆動軸が曲線の内側に存在する場合と、曲線の外側に存在する場合との場合わけが必要となります。
私の入手したShayの図面で確認した範囲では、エンジンから前方の台車に動力を伝える駆動軸の寸法と、エンジンから後方の台車に動力を伝える駆動軸の寸法とは異なります。ただし、これはそれぞれについて\(\alpha\)と\(\beta\)とを求めればよいと言う事ですので、計算の方法には影響がありません。下記の議論では片方のみを取り上げます。
もう一つお断りしておくと、3(4)トラックShayになると更に2(4)つのユニバーサルジョイントを介して、後方の台車に動力が伝えられます。ここまで議論してきた事を応用すれば解析は可能ですが、今回の議論の対象外とします。
下に示したのは、半径\(r\)の円弧上をShayが走行しており、駆動軸が円弧の内側(円弧の中心に近い側)にあるときの図です。
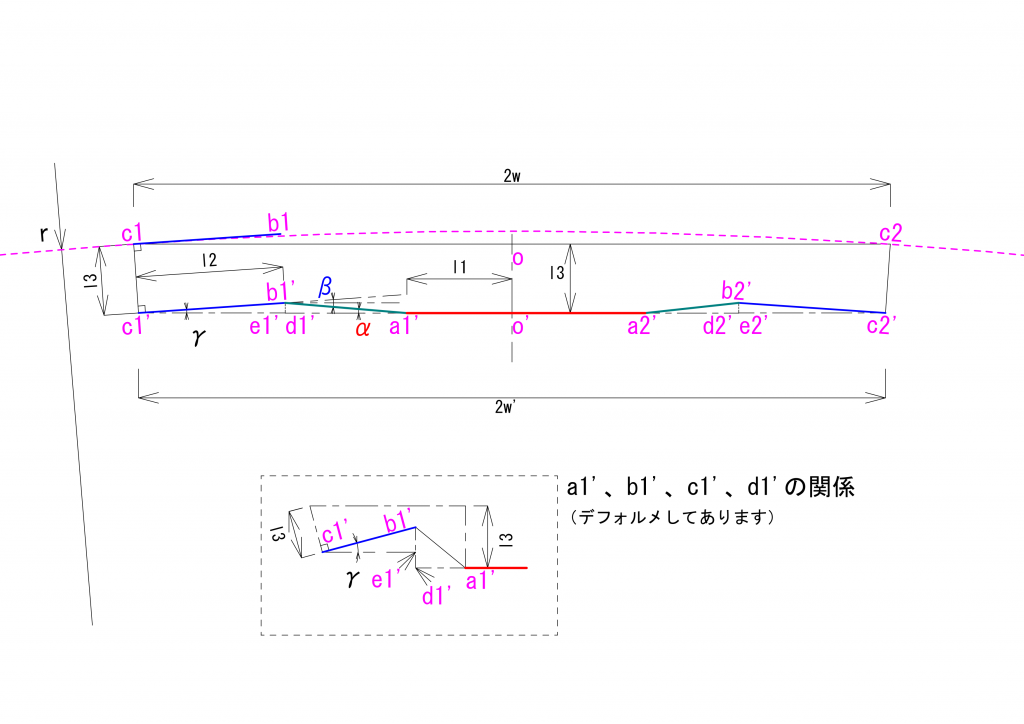
MPギアの場合と同様、\(c_1\)と\(c_2\)とが台車の中心を、\(o\)が\(c_1\)、\(c_2\)との中心点を示します。また、線分\(c_1c_2\)の長さを\(2w\)とします。MPギアの場合と同様、台車の線路方向の中心軸は、円弧上の\(c_1\)と\(c_2\)とで接すると言う仮定をおきます。\(c_1\)に接する線分\(c_1b_1\)は、\(c_1\)と円弧の中心\(O_r\)(注:図には示していません)とを結んだ線と直交するということです。
Shayの駆動軸が車体中心に対してどれだけオフセットしているかの寸法を\(l_3\)とします。
\(o’\)は駆動軸の中心位置を、\({a_1}’\)、\({a_2}’\)はエンジン側のユニバーサルジョイントの位置を、\({b_1}’\)、\({b_2}’\)は台車側のユニバーサルジョイントの位置を示します。\({c_1}’\)、\({c_2}’\)は、それぞれ\(c_1\)、\(c_2\)から、円弧の中心\(O_r\)に向かって長さ\(l_3\)の線分を引いた位置を示します。
MPギアと異なり、\(o’\)、\({a_1}’\)、\({a_2}’\)を結ぶ直線状に\({c_1}’\)、\({c_2}’\)は存在しません。\({a_1}’\)、\({a_2}’\)から垂線を下した時に、\({a_1}’\)、\({a_2}’\)を通る直線と交差する点をそれぞれ\({d_1}’\)、\({d_2}’\)と、\({c_1}’\)、\({c_2}’\)を通る直線と交差する点をそれぞれ\({e_1}’\)、\({e_2}’\)とします。
線分\(o'{a_1}’\)の長さを\(l_1\)、線分\({b_1}'{c_1}’\)の長さを\(l_2\)、線分\({c_1}'{c_2}’\)の長さを\(2w’\)とします。線分\({c_1}'{e_1}’\)と線分\({c_1}'{b_1}’\)とのなす角を\(\gamma\)、線分\({a_1}'{b_1}’\)と線分\({a_1}'{d_1}’\)とのなす角度を\(\alpha\)、線分\({b_1}'{a_1}’\)と線分\({c_1}'{b_1}’\)を車体の中心方向に延長した線とのなす角を\(\beta\)とします。
このような前提で\(\alpha\)、\(\beta\)を求めます。まず、円弧の中心\(O_r\)と\({c_1}\)と\(o\)とがなす三角形と、円弧の中心\(O_r\)と\({c_1}’\)と、\({c_1}'{e1}’\)を車体の中心方向に延長した線と\(O_r\)、\(o\)を通る直線との交点とがなす三角形とは相似ですので、MPギアの場合と同様、
\(cos(\gamma)=\frac{w}{r}\)
が成り立ちます。
また、上記2つの三角形が相似であるということは、\(w:r =w:'(r-l_3)\)が成立するということですので、
\(w’=w\cdot\frac{r-l_3}{r}\)
が成り立ちます。
次は\(\alpha\)を求めます。
まず、線分\({a_1}'{d_1}’\)の長さは、\(w’-l_1-l_2\cdot cos(\gamma)\)となります。
線分\({b_1}'{d_1}’\)の長さは、線分\({b_1}'{e_1}’\)の長さ\(l_2\cdot sin(\gamma)\)と、線分\({e_1}'{d_1}’\)の長さ\(l_3 – l_3\cdot cos(\gamma)\)との和、\(l_2\cdot sin(\gamma)+l_3 – l_3\cdot cos(\gamma)\)となります。
\({a_1}’\)、\({b_1}’\)、\({e_1}’\)のなす直角三角形に注目すると、
\(tan(\alpha)=\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w’-l_1-l_2\cdot cos(\gamma)}\)
\(=\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w\cdot\frac{r-l_3}{r}-l_1-l_2\cdot cos(\gamma)}\)
が成り立ちます。
従って、半径\(r\)の円を走行中のShayのユニバーサルジョイントの\(\alpha\)と\(\beta\)とは、
\(\gamma=cos^{-1}(\frac{w}{r})\)
\(\alpha=tan^{-1}(\frac{l_2\cdot sin(\gamma)+l_3-l_3\cdot cos(\gamma)}{w\cdot\frac{r-l_3}{r}-l_1-l_2\cdot cos(\gamma)})\)
\(\beta=\alpha+\gamma\)
と求める事ができます。
次は、下図のように駆動軸が円弧の外側に来た場合の式を考えてみます。
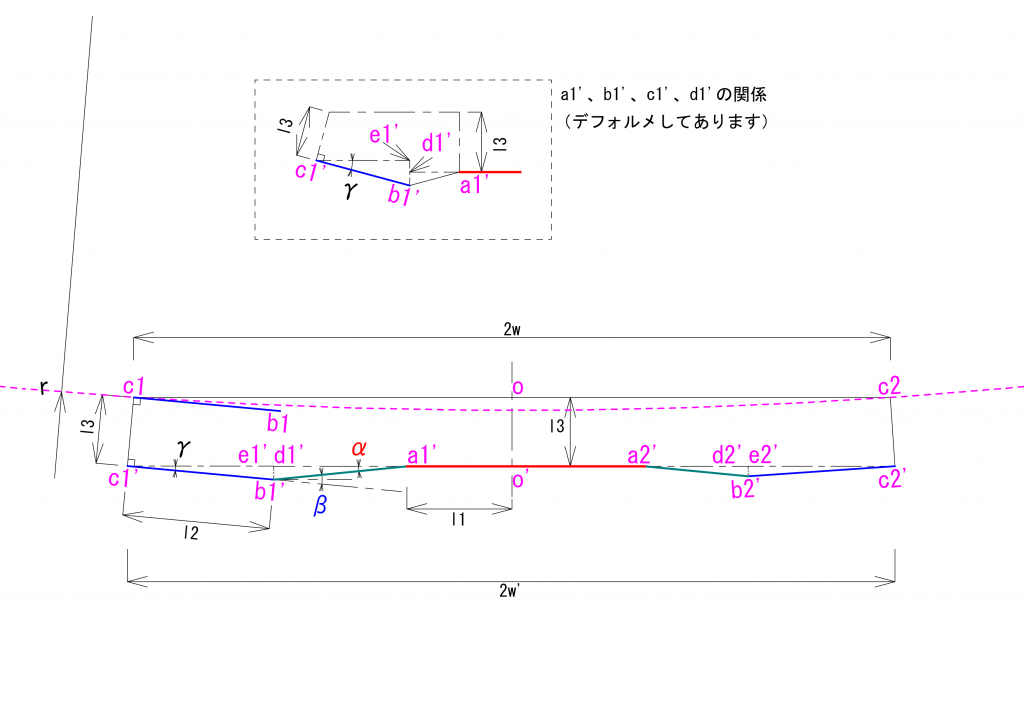
座標や長さの考え方は、駆動軸が円弧の内側に来た場合と同じですので省略し、\(\alpha\)、\(\beta\)、\(\gamma\)をさっそく求めてみます。
円弧の中心\(O_r\)と\({c_1}\)と\(o\)とがなす三角形と、円弧の中心\(O_r\)と\({c_1}’\)と、\({c_1}'{e1}’\)を車体の中心方向に延長した線と\(O_r\)、\(o\)とを通る直線との交点と、がなす三角形とは相似ですので、
\(cos(\gamma)=\frac{w}{r}\)
が成り立ちます。また、上記2つの三角形の相似であるということは、\(w:r =w’:(r+l_3)\)が成立するということですので、
\(w’=w\cdot\frac{r+l_3}{r}\)
が成り立ちます。
線分\({a_1}'{d_1}’\)の長さは\(w’-l_1-l_2\cdot cos(\gamma)\)となります。線分\({b_1}'{d_1}’\)の長さは、線分\({b_1}'{e_1}’\)の長さ\(l_2\cdot sin(\gamma)\)から線分\({e_1}'{d_1}’\)の長さ\(l_3 – l_3\cdot cos(\gamma)\)を引いた、\(l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)\)となりますので、
\(tan(\alpha)=\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w’-l_1-l_2\cdot cos(\gamma)}\)
\(=\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w\cdot\frac{r+l_3}{r}-l_1-l_2\cdot cos(\gamma)}\)
が成立します。これらの式から、
\(\gamma=cos^{-1}(\frac{w}{r})\)
\(\alpha=tan^{-1}(\frac{l_2\cdot sin(\gamma)-l_3+l_3\cdot cos(\gamma)}{w\cdot\frac{r+l_3}{r}-l_1-l_2\cdot cos(\gamma)})\)
\(\beta=\alpha+\gamma\)
と導き出すことができます。
次回はこれらの式に具体的な数値を当てはめてみたいと思います。