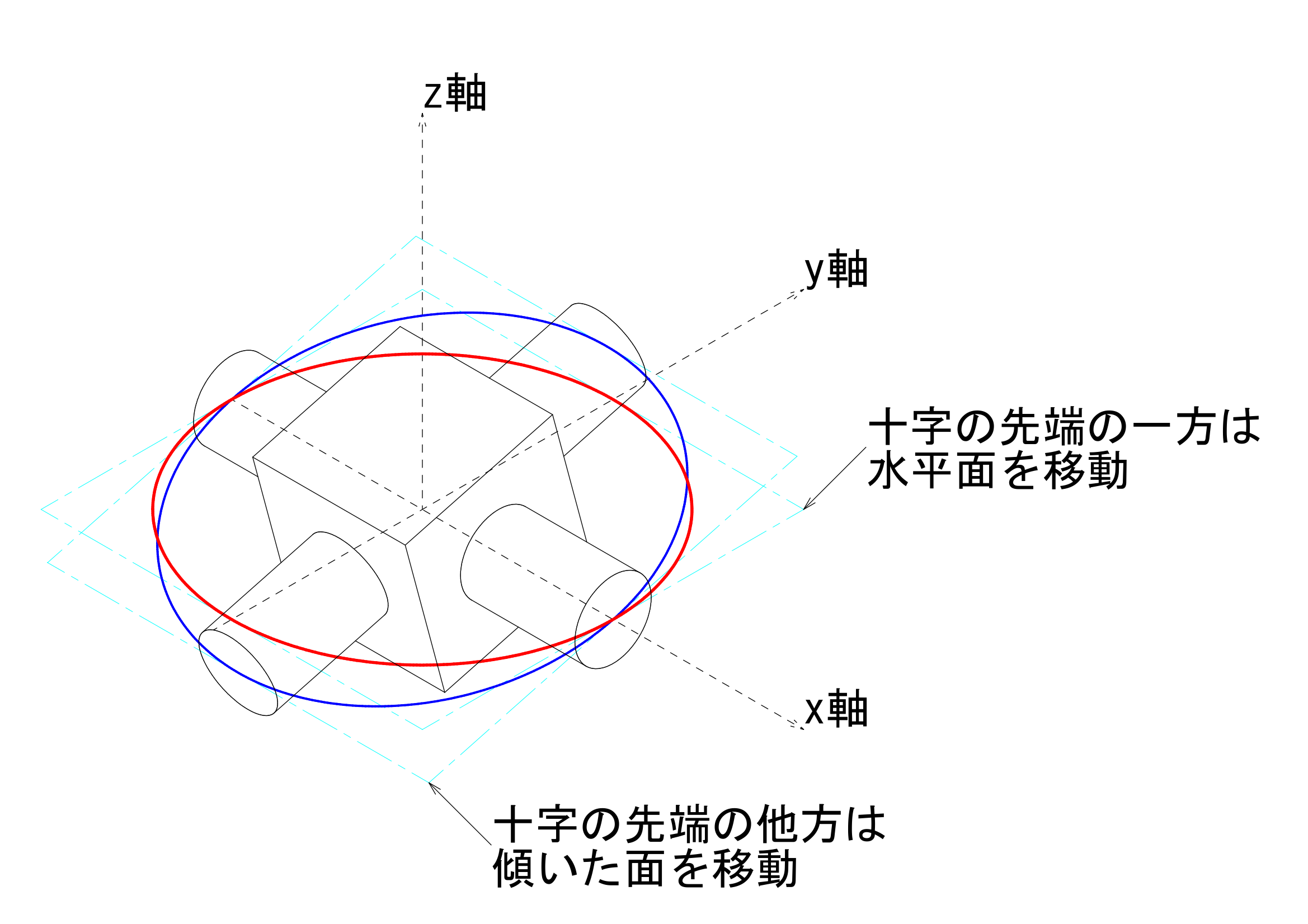
ユニバーサルジョイントを構成する十字型の部品の2つの軸の先端がどこを動くか、を示したのが次の図となります。ここで、十字型の部品の中心、つまり、２つの軸が交差する点を原点\((0,0,0)\)とします。また、水平面上（赤い円）を移動する軸に取り付けられたフォーク状の部品に動力が供給され、それが傾いた面上（青い円）を移動する軸に伝達されるとします。ここでは仮に、水平な面を「駆動面」と、傾いた面を「伝達面」と呼ぶこととします。

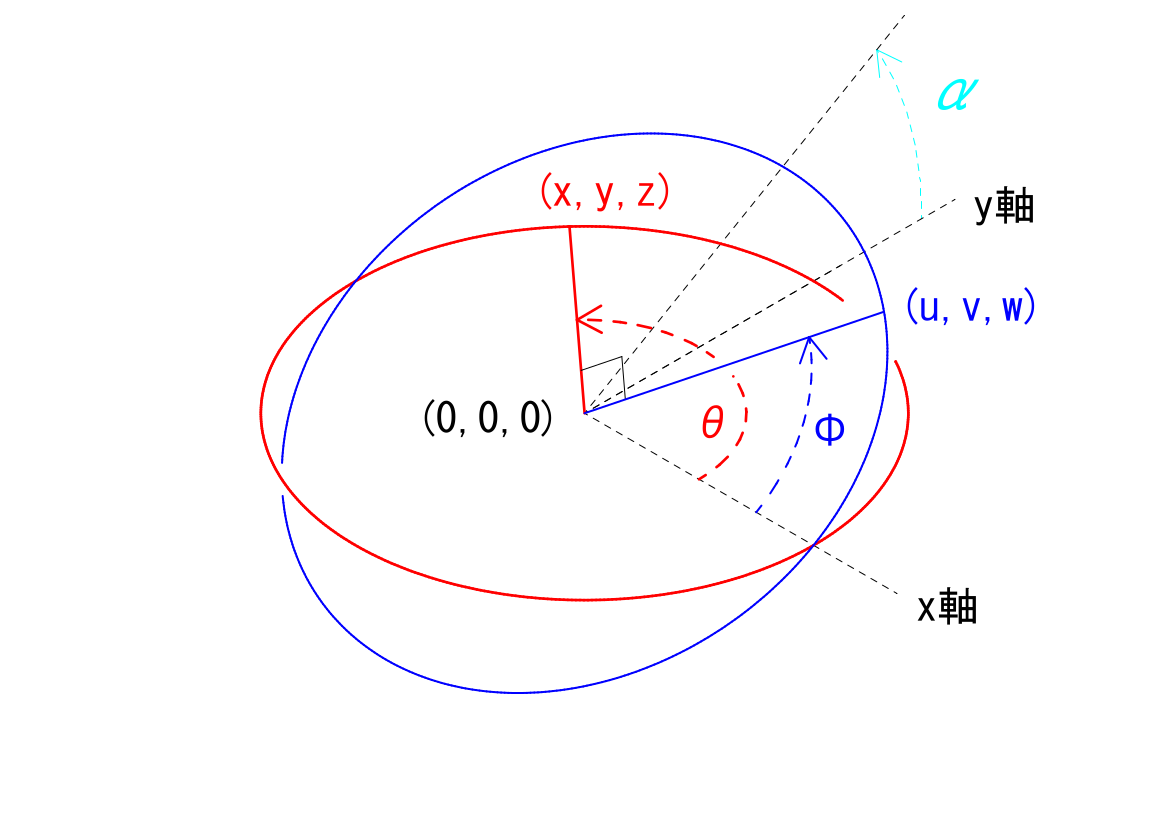
原点と十字の二軸のそれぞれの一方の先端だけに注目したのが、次図です。以下、この注目した軸の先端を「基準点」と呼ぶこととします。基準点の選び方によって、多少式が変わってきますが、最終的には同等の結果が得られます。

駆動面を動く基準点は、原点\((0,0,0)\)を中心に、水平面上の半径\(r\)の円を回転し（上図の赤い円）、伝達面を動く基準点は、原点を中心に、駆動面に対して角度\(\alpha\)傾いた面の上の半径\(r\)の円を回転します（同じく青い円）。

このとき、駆動面の基準点の座標を\((x,y,z)\)、伝達面の基準点の座標を\((u,v,w)\)であるとします。更に、\((x,y,z)\)の駆動面における\(x\)軸に対する角度を\(\theta\)とし、\((u,v,w)\)の伝達面における\(x\)軸に対する角度を\(\varphi\)とします。

駆動面の基準点の座標は、三角関数の定義から、

\((x,y,z)=(r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

となります。

伝達面の基準点の座標を求めると、まず\(x\)座標の値\(u\)は、被駆動面の傾きによらず、

\(u = r\cdot cos(\varphi)\)

となります。

座標\((u,v,w)\)と座標\((u,0,0)\)の距離は、\(r\cdot sin(\varphi)\)となります。座標\((u,0,0)\)、\((u,v,0)\)、\((u,v,w)\)からなる直角三角形を考えると、この底辺の長さ、高さがそれぞれ\(u\)、\(v\)となり、伝達面の傾きが\(\alpha\)なので、

\(v = r\cdot sin(\varphi)\cdot cos(\alpha)\)

\(w = r\cdot sin(\varphi)\cdot sin(\alpha)\)

となります。まとめると、

\((u,v,w) = (r\cdot cos(\varphi), r\cdot sin(\varphi)\cdot cos(\alpha), r\cdot sin(\varphi)\cdot  sin(\alpha))\)

となります。