このシリーズは５~6回で終わるつもりにしていました。が、書いておいた方がよいかと思うことは次々に出てくるもので、前回まで引っ張り、ようやくおしまいと思っていたところ、またまたネタが出てきたので、あと数回続きます。ここまでの詳細な議論に興味のある方は限られていると思いますが、どこかで参考となる場面があれば幸いです。

さて、2つのユニバーサルジョイントを同位相で組み合わせ、\(|\alpha| = |\beta|\)とした場合に、駆動面と最終駆動面との基準点の角度は一致し、角速度が一致するということを述べてきました。この\(|\alpha| = |\beta|\)となる条件をもう少し具体的に見てみます。

まず考えられるのは、次の図のような場合です。ここで、右側の\(\alpha\)傾いた軸に動力源がつながり、左側の\(\beta\)傾いた軸に最終的に動力が伝達されると考えてください。また、\(\alpha\)が右下に傾き、\(\beta\)が上に傾く場合、つまりはこの図を上下に対称にひっくり返した場合は、ここでの議論と等価となりますので省略します。なお、前回と同様、\(\alpha\)、\(\beta\)とも、2つの軸のなす角度を示していますが、これらは、駆動面と伝達面とのなす角度、中継面と最終伝達面とのなす角度と同じです。

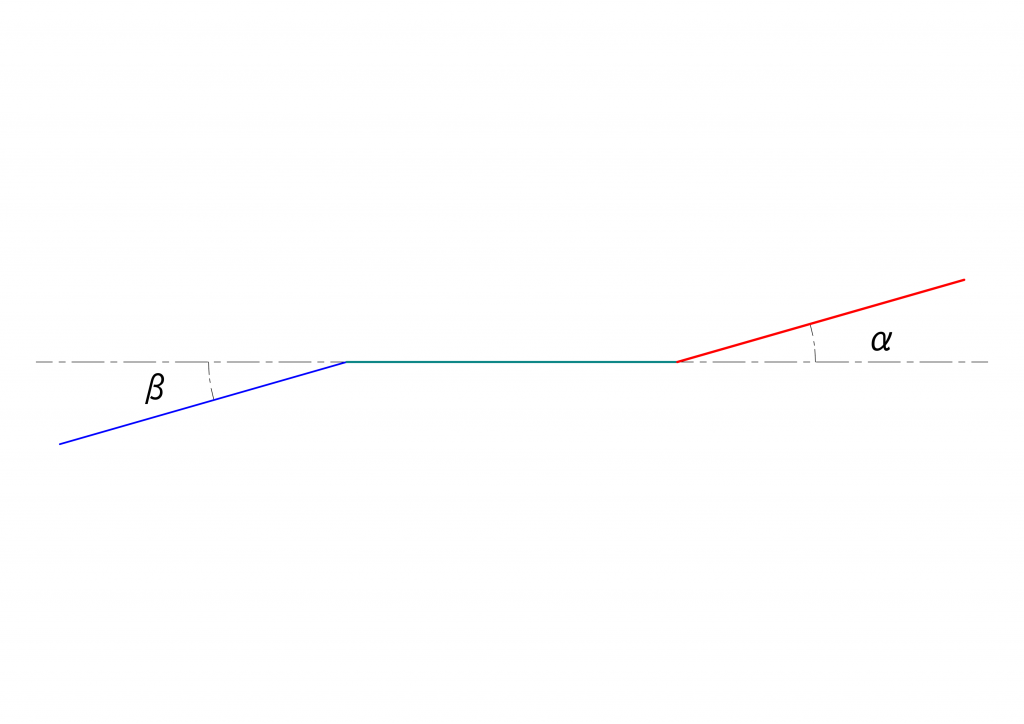
このような状態では、2つの傾いた軸は平行となります。平行な2つの線に交わる線を引いたときに錯角が等しい、というというのは中学校の数学で習う項目でした。

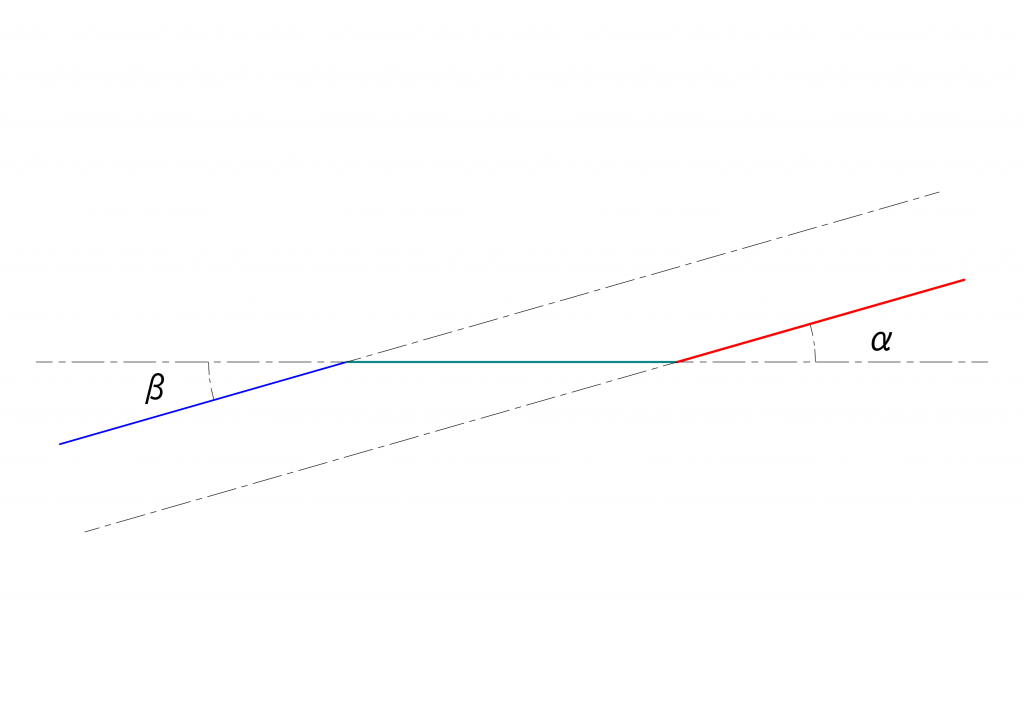
このことは、モーターにつながる軸と、車輪・ギアのつながる軸を絶えず平行になるようにしておけば、\(|\alpha| = |\beta|\)を実現できる、ということを意味しています。ただ、このような条件を満たすような場合は、模型に関して言えば限られるのではないかと思います。

もう一つ考えられるのは、次のような場合です。上と同様に、右下に\(\alpha\)傾いた軸に動力源がつながり、左上に\(\beta\)傾いた軸に最終的に動力が伝達されると考えてください。また、この図を上下に対称に反転させた場合も等価の議論ができますので省略します。

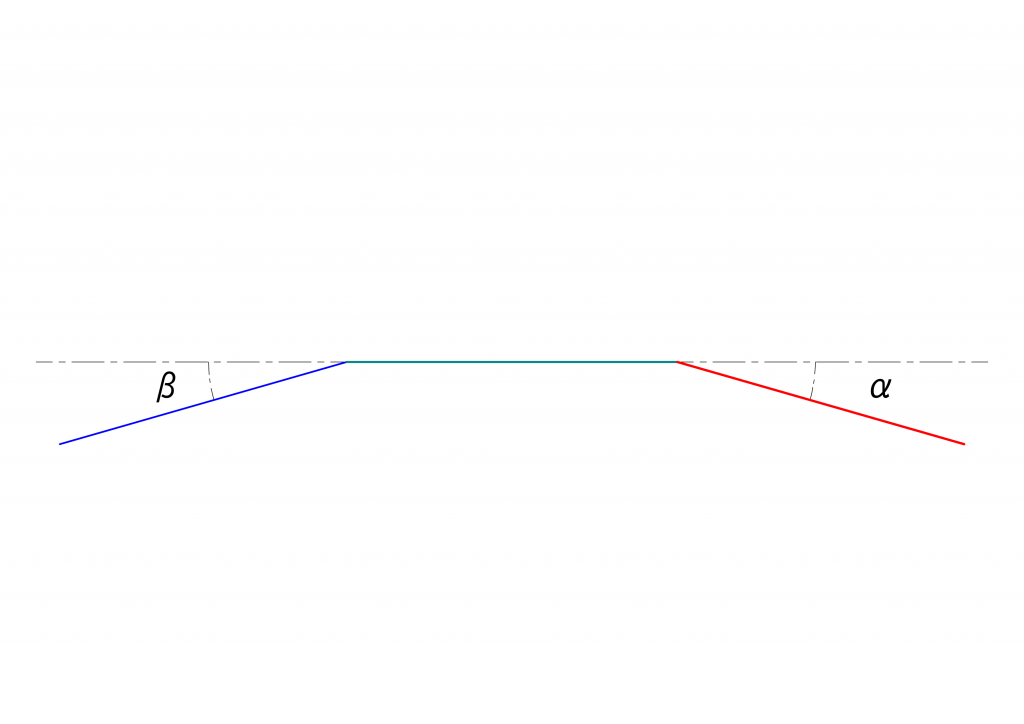
これが成立するのは、\(\alpha\)傾いた軸と、\(\beta\)傾いた軸と、水平の軸（２つのユニバーサルジョイントをつなげる軸）とが、二等辺三角形をなす場合であると言い換えることができます。

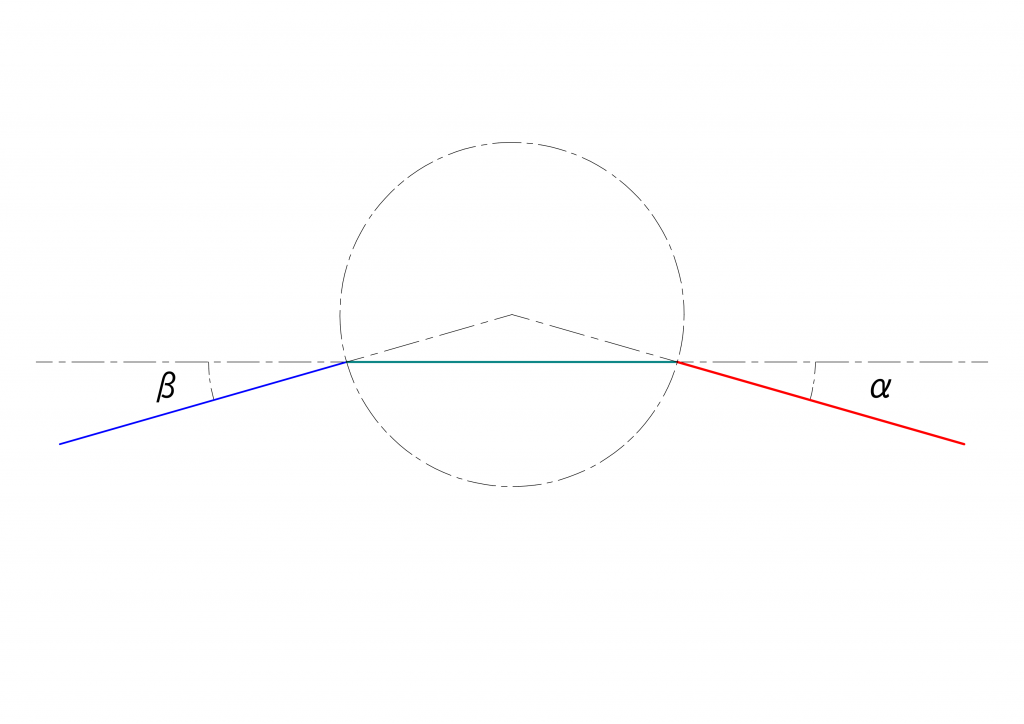
\(\alpha=\beta\)が成立するいくつかの例を次の図に示します。ここでは、右側の軸を水平に固定しましたが、これは模型を念頭に、モーターの伝わる軸は（車体に対して）固定されており、左側の軸がボギー台車につながっており、最終的に何らかの手段で車輪を駆動する、ということを想定しています。

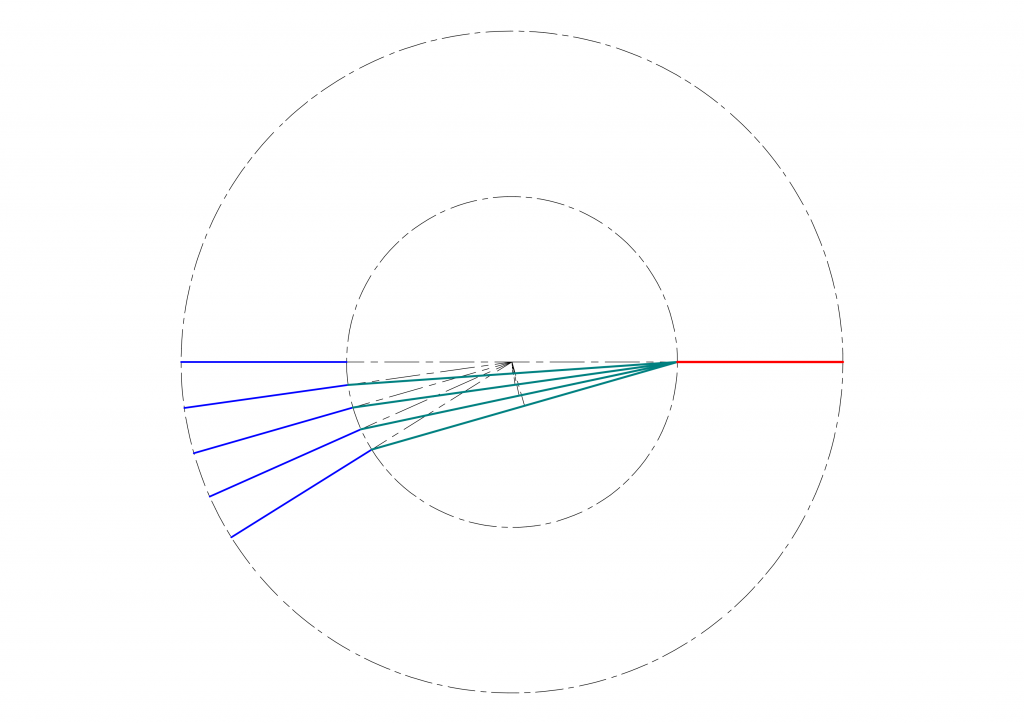
この図はどういうことを示しているかというと、台車の回転する中心から等距離にユニバーサルジョイントを置くような配置ができれば、\(|\alpha|=|\beta|\)を実現することができる、ということです。

ただ、HO/16番クラスでは、ユニバーサルジョイントの距離を十分に確保できるような駆動系の配置をとることができるか、という問題が出てくると思われます。またゲージにかかわらず、駆動系のメカニズムが台車と干渉しないように駆動軸全体を床より高いところに位置させる必要がでてきます。従って、このような配置を実用的に使うことのできる場合がどの程度あるのかは、やや疑問ではあります。