模型にはほとんど関係のない話ですが、自分自身の備忘録のために書き残しておくこととします。大部分の方には興味のない話と思われますので、読み流してください。この分野の造詣は深くはありませんので、説明が不十分であったり、不適切な表現があることがありますが、ご容赦ください。

橋を設計する中で、橋の部材には圧縮部材と伸張部材があるということを理解しました。この部材の圧縮、伸張の力をどのように計算するか、ということに興味を持ち、いくつか例題を作って解いてみたというお話です。

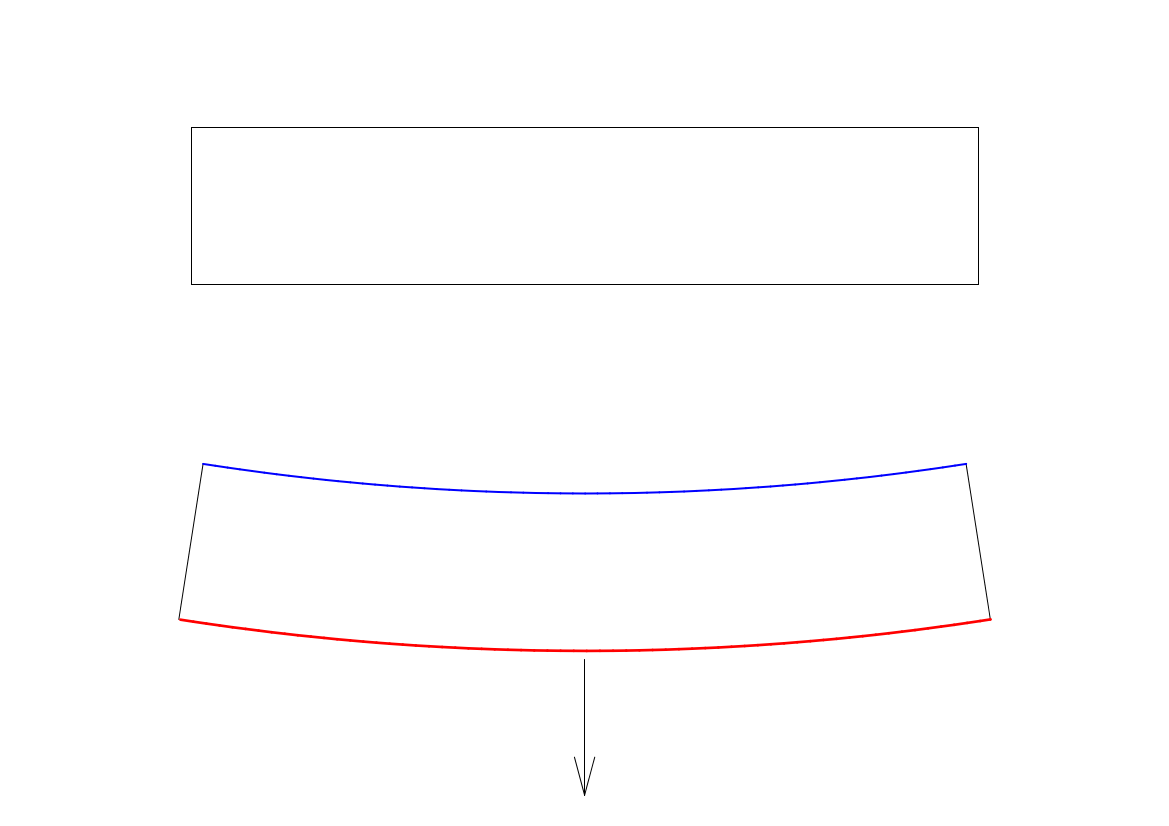
話を単純化して、橋を一本の棒とみなし、その棒に下向きの荷重がかかるとすると、下のように曲がろうとします。この時、橋の下辺には伸張力が加わるために延び、橋の上辺には圧縮力が加わり、縮みます。

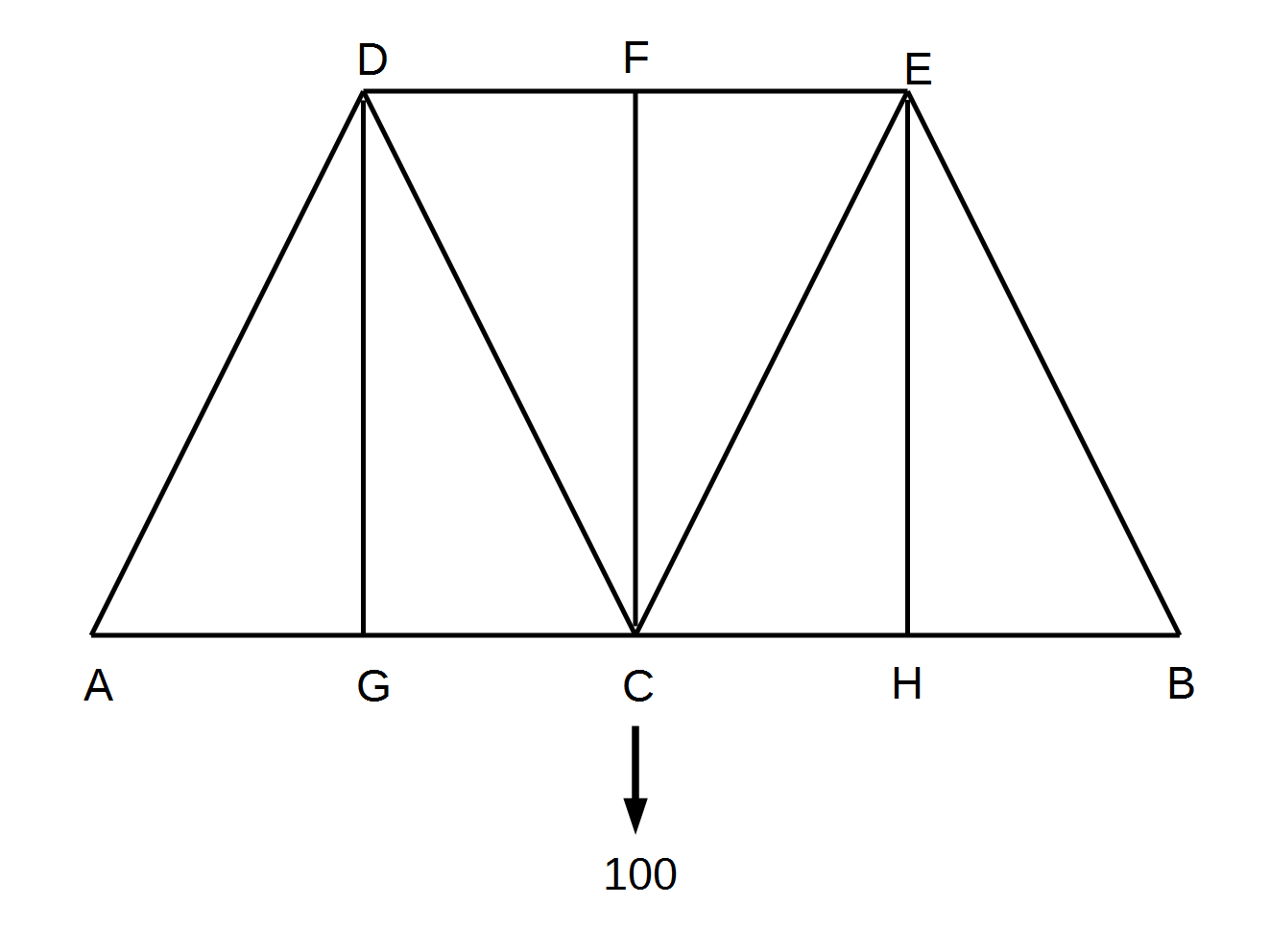
実際の橋にかかる力を計算するには、下図のように、橋の構造を描き、力のかかる場所を決めて、橋の構造部材が集まる節点にどのような力が加わるかを計算してゆけばよいことになります。

力のかかり方を計算する際のルールは単純で、下図に示す通り、節点に集まる力の総和がゼロになるということです。

具体的には、節点に集まる部材の水平方向（\(x\)軸方向）の力の総和、同じく垂直方向（\(y\)軸方向）の力の総和、のいずれもが\(0\)になるようにすればよい、ということです。

上記の例では、\(F_1\)と\(F_2\)の垂直方向との力の和が\(0\)となります。したがって\(F_2\)の角度を\(\theta\)とすると、

\(F_1 – F_2 \times sin(\theta) = 0\)

が成り立ちます。同様に、垂直方向については、

\(-F_2 \times cos(\theta) + F3 = 0\)

が成り立ちます。

このような式を、力が分っている節点に注目して解きます。言い換えると、解けるところから解いてゆく、ということです。この時、矢印の方向が分らない場合がありますが、その際はどちらかの方向を仮定して計算し、マイナスとなったら、矢印の方向を反転させます。

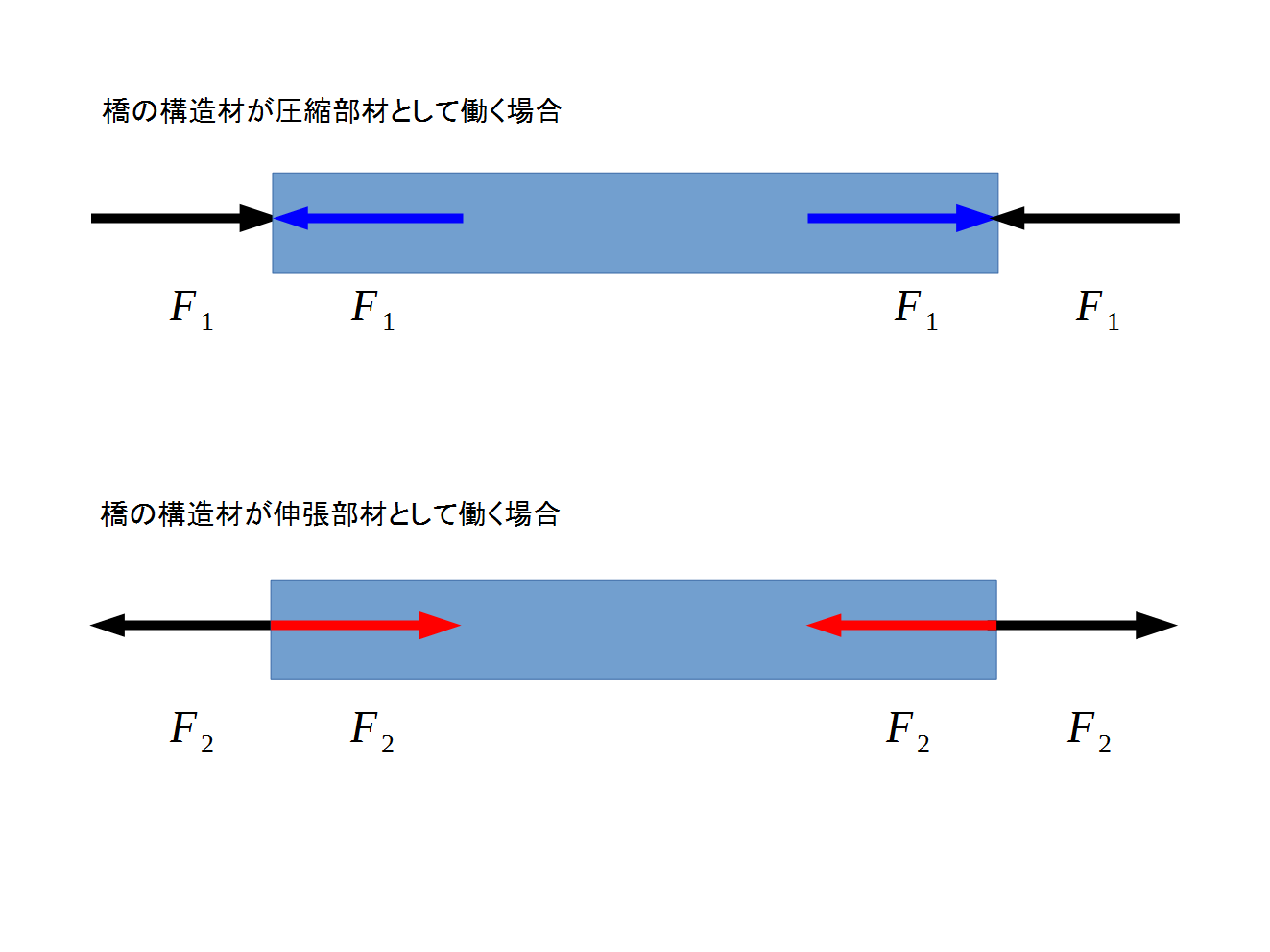
一つの節点の力のかかり方がわかったら、構造部材の反対側にその力とは反対方向の力がかかります。例えば、下図上のように、左側の節点に外向きに働く力が働いたら（左向きの青い矢印）、右側の節点には反対向きの力を加えます（右向きの青い矢印）。同様に下図下のように、左側の節点に内向きに働く力が働いたら（右向きの赤い矢印）、右側の節点には反対向きの力を加えます（左向きの赤い矢印）。

こうすると、次に解くことのできる節点が出てきますので、そこにかかる力を解き、ということを丹念に繰り返せば、全体として橋にかかる力が計算できます。

最終的に橋のすべての部材にかかる力が分った場合、上の図の青い矢印のような部材は圧縮部材、赤い矢印のような部材は伸張部材として働くことがわかります。この部材に働く力だけ見ると圧縮・伸張という言葉と混乱しますが、これは部材の内部に働く力に注目するからであって、外からこの部材にどういう力が加わるか、という観点で見る必要があります。

次回以降、簡単な例題を作って解いてみます。