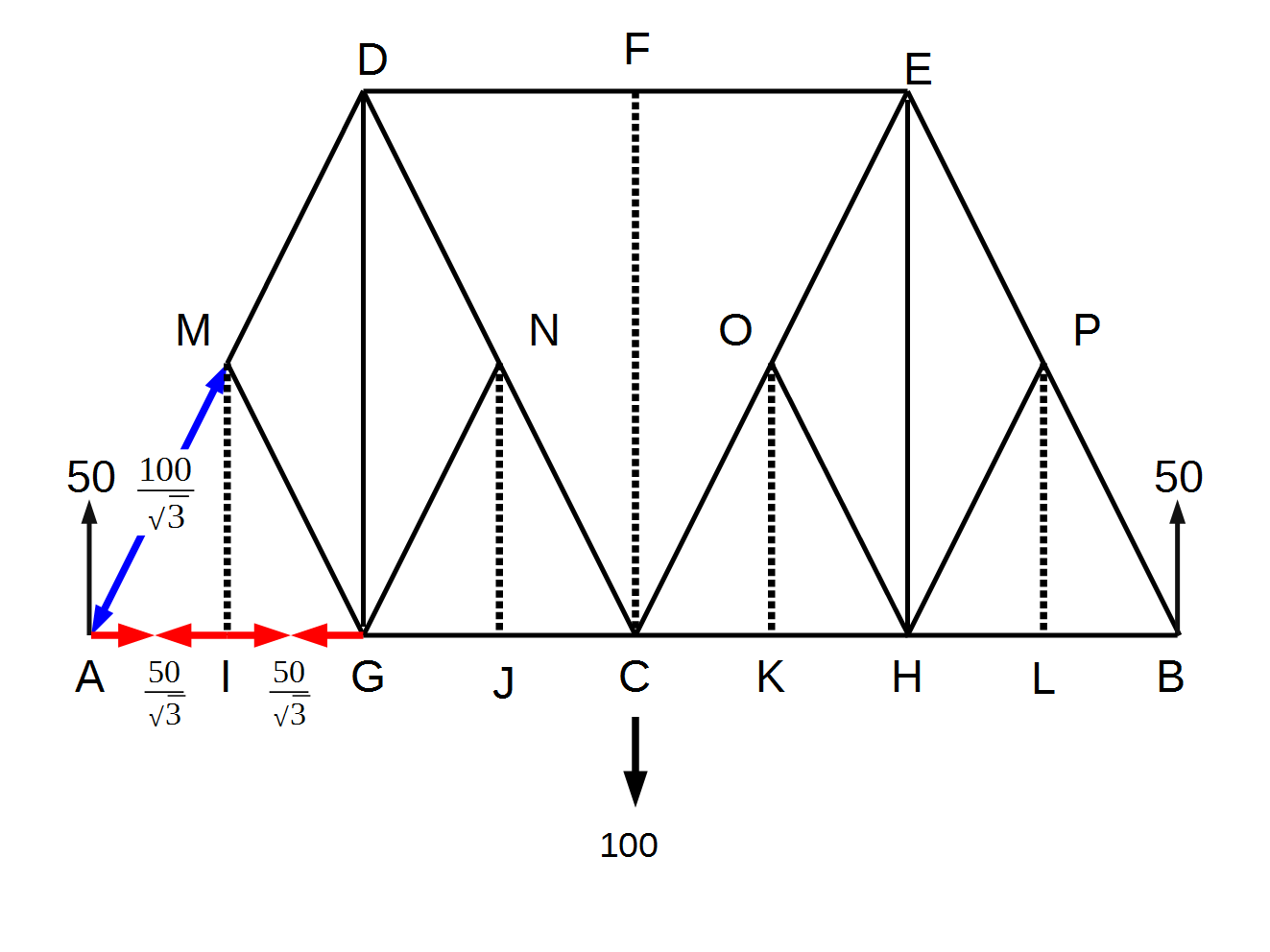
今回は、前回と同様の計算をBaltimore Truss Bridgeで行ってみます。前回同様、橋の中心（C点）に下向きの100の力がかかると、橋の下辺の両端であるA点、B点には上向きの50の力がかかり、A-M、A-Iの構造材にかかる力は前回と同じ計算で求めることができます（下図参照）。

また、I点、J点、F点、K点、L点には、垂直方向の力を持ちうる部材が1つしかありませんから、M-I、N-J、F-C、O-K、P-Lの構造材はZero Force Memberであることがわかります。

更に、M-Iの部材がZero Force Memberですので、I-GのI点には、A-IのI点と反対向きで同じ大きさの力が加わります。

ここでM点に注目して力のかかり方を一般的な場合で計算してみると、つぎのようなことがわかります。

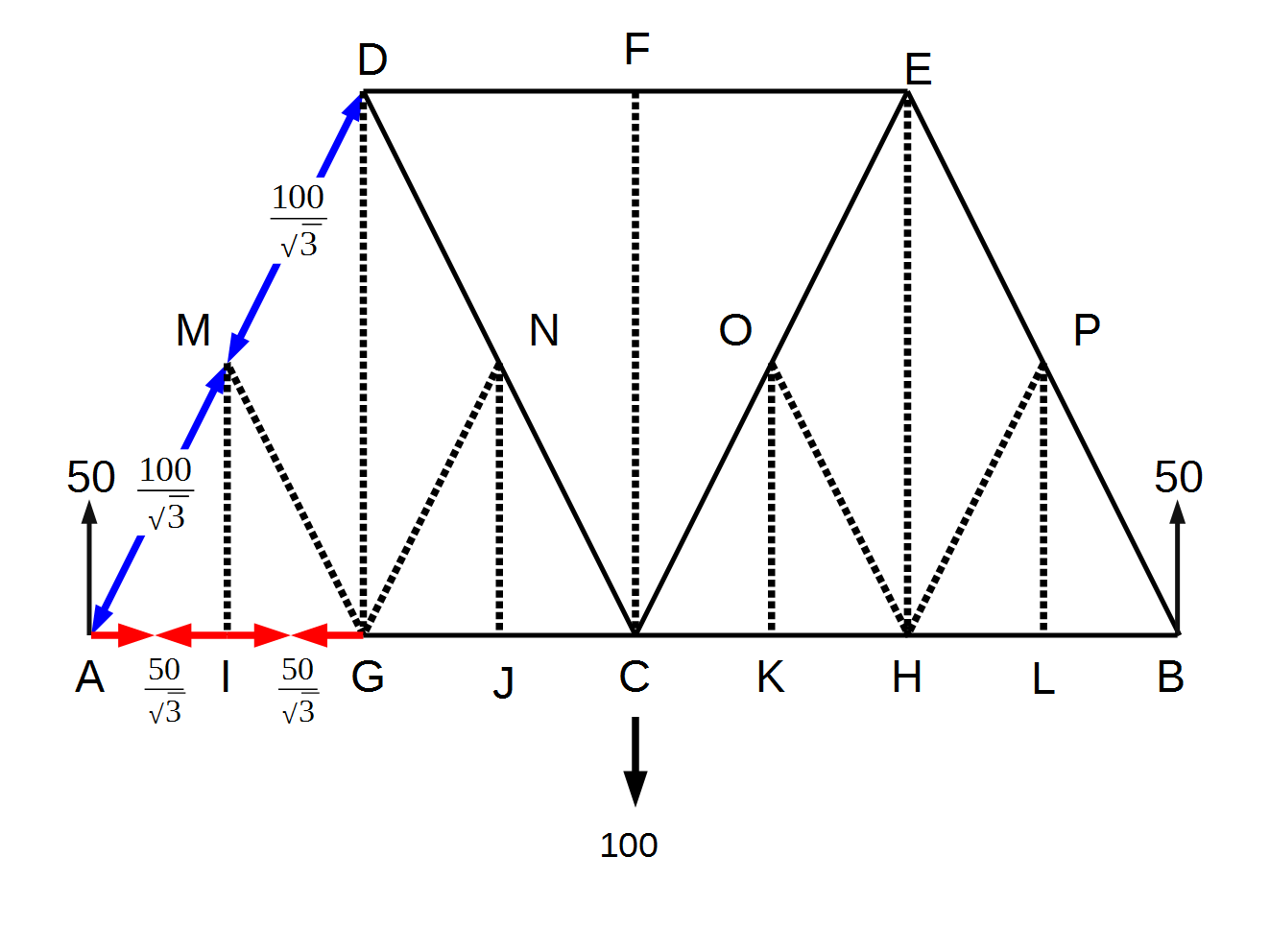
つまり、Baltimore Truss Bridgeの特徴的な小さなトラス構造の縦の部材がZero Force Memberであった場合は、その小さなトラス構造の斜材もZero Force Memberとなる、ということです。最初の図で言うと、M-IがZero Force Memberであれば、M-GもZero Force Memberとなります。同様にN-G、O-H、P-HもZero Force Memberとなります。

また、大きなトラスを構成する斜材に注目すると、小さなトラス構造の頂点を境に反対向きで同じ大きさの力が加わる、ということになります。これらを考慮したのが下の図です。

ここまで来ると、今回考えているように中心にのみ力がかかる場合、Baltimore Truss Bridge特有の小さなトラス構造は構造的には何も寄与せず、Pratt Truss Bridgeと等価となる、ということがわかります。したがって、最終的に以下のような結果を得ます。