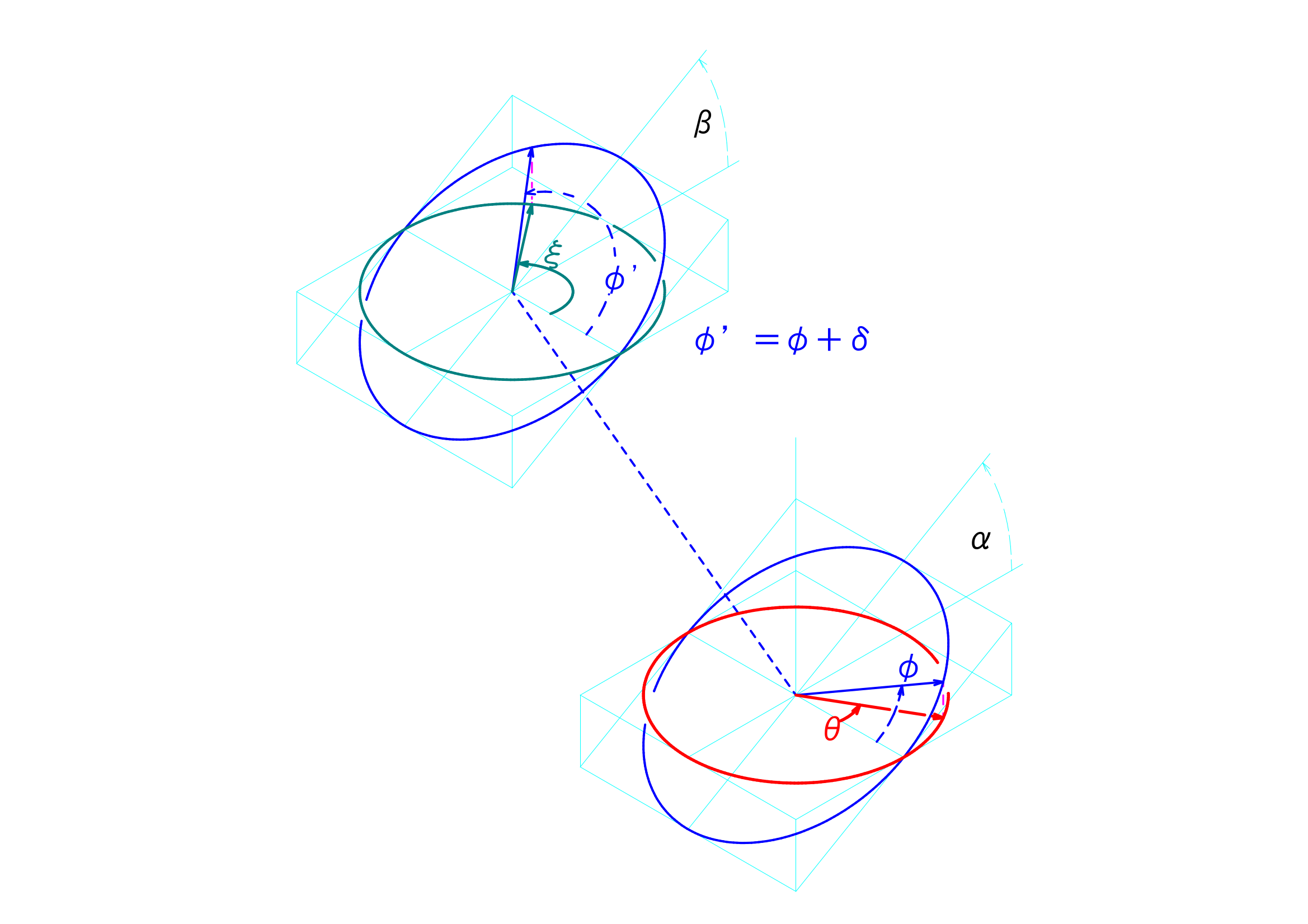
簡易型ユニバーサルジョイントを2つ組み合わせた場合の解析を行います。正規型ユニバーサルジョイントを２つ組み合わせた図と同様のものを下記に示します。

前回の議論から、駆動面（赤の円）を移動する基準点の\(x\)軸に対する角度\(\theta\)と、伝達面（青の楕円）を移動する基準点の\(x\)軸に対する角度\(\varphi\)との間には次のような関係が成立します。

\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)

中継面（もう一つの青の楕円）を移動する基準点の\(x\)軸に対する角度\(\varphi^\prime\)と、最終伝達面（緑の円）を移動する基準点の\(x\)軸に対する角度を\(\xi\)とすると、\(\theta\)と\(\varphi\)との関係と同じ考え方で、

\(tan(\varphi^\prime) = tan(\xi)\cdot\frac{1}{cos(\beta)}\)

を得ることができます。

一点細かいことを補足しておくと、正規型ユニバーサルジョイントでは、動力を受ける側も伝える側も対称の関係にありましたので、\(\beta\)は、中継面（上の青い円）を基準とした角度としていましたが、簡易型ユニバーサルジョイントは対称ではありませんので、最終伝達面（上の緑の円）を基準とした角度としています。

さて、\(tan(\alpha+\beta)=\frac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)\cdot tan(\beta)}\)でしたので、

\(tan(\varphi^\prime) = tan(\varphi +\delta) = \frac{tan(\varphi)+tan(\delta)}{1-tan(\varphi)\cdot tan(\delta)}\)

となり、\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)を代入し、

\(tan(\varphi^\prime) = \frac{tan(\theta)\cdot\frac{1}{cos(\alpha)}+tan(\delta)}{1-tan(\theta)\cdot\frac{1}{cos(\alpha)}\cdot tan(\delta)}\)

分子と分母とに\(cos(\delta)\cdot cos(\alpha)\)をかけ、

\(tan(\varphi^\prime) = \frac{tan(\theta)\cdot cos(\delta) + sin(\delta)\cdot cos(\alpha)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\)

最終的に、

\(tan(\xi) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta)\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\cdot cos(\beta)\)

を得ます。

正規型ユニバーサルジョイントの時と同様に、我々の興味のあるのは、\(\delta=0\)もしくは\(\delta=\frac{\pi}{2}\)の時です。

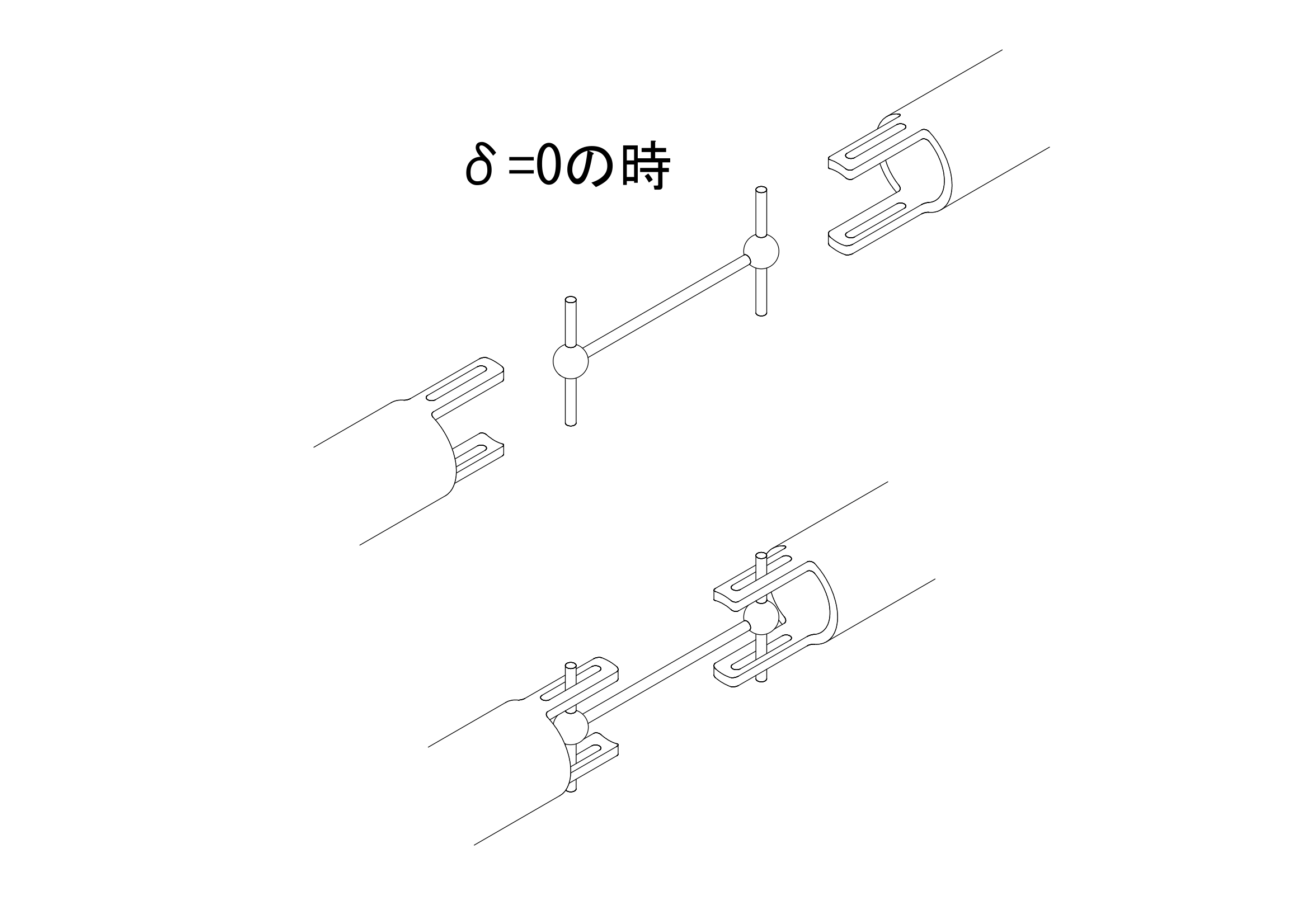
\(\delta=0\)の時は、下図のとおり、２つのピンが同位相となります。

この時、\(sin(\delta)=0\)、\(cos(\delta)=1\)ですので、

\(tan(\xi) = tan(\theta)\cdot \frac{cos(\beta)}{cos(\alpha)}\)

従って、\(|\alpha| = |\beta|\)であれば、\(\theta\)と\(\xi\)とは絶えず同じ角度であることがわかります。

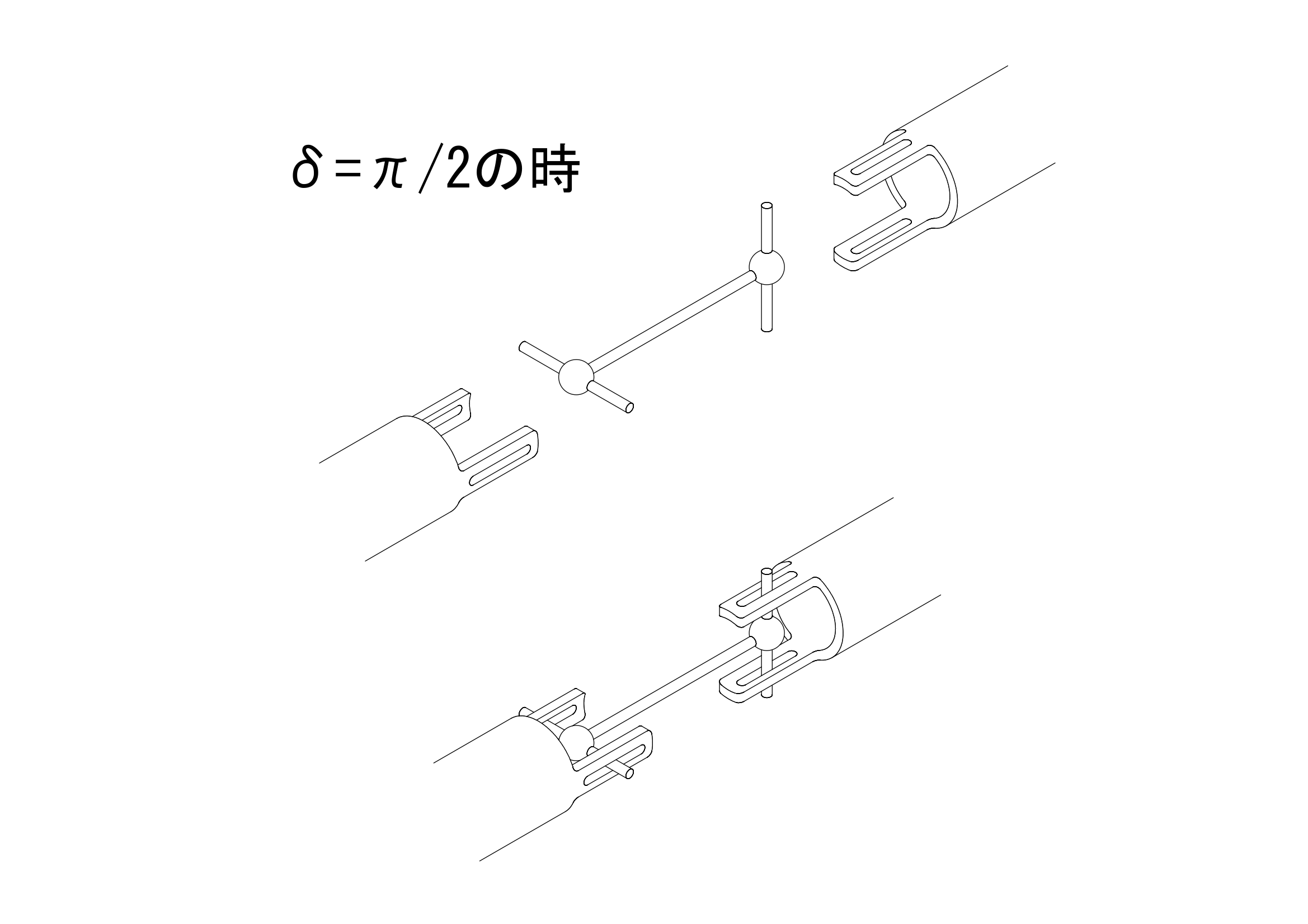
\(\delta=\frac{\pi}{2}\)の時は、下図のとおり、２つのピンの位相が90°ずれます。

この時、\(sin(\delta)=1\)、\(cos(\delta)=0\)ですので、

\(tan(\xi) = -\frac{1}{tan(\theta)}\cdot cos (\alpha)\cdot cos(\beta)\)

\(= tan(\theta-\frac{\pi}{2})\cdot cos (\alpha)\cdot cos(\beta) \)

という関係を得ます。正規型ユニバーサルジョイントの場合と同様、\(\theta\)と\(\xi\)は、同じ角度ではないことがわかります。