前々回、前回と、ユニバーサルジョイントの3つの軸が同一平面に存在しない場合を仮定して、角速度がどのように変動するかの具体例をMPギアを例として計算してみました。今回はこれをShayの場合で考察してみます。解析の対象としたのは、前に紹介したGreenbrier, Cheat and Elk Railroadの12号機（おそらくsn3156)です。

1922年版のLocomotive cyclopedia of American practiceに載っている主要寸法を次の図に示します。

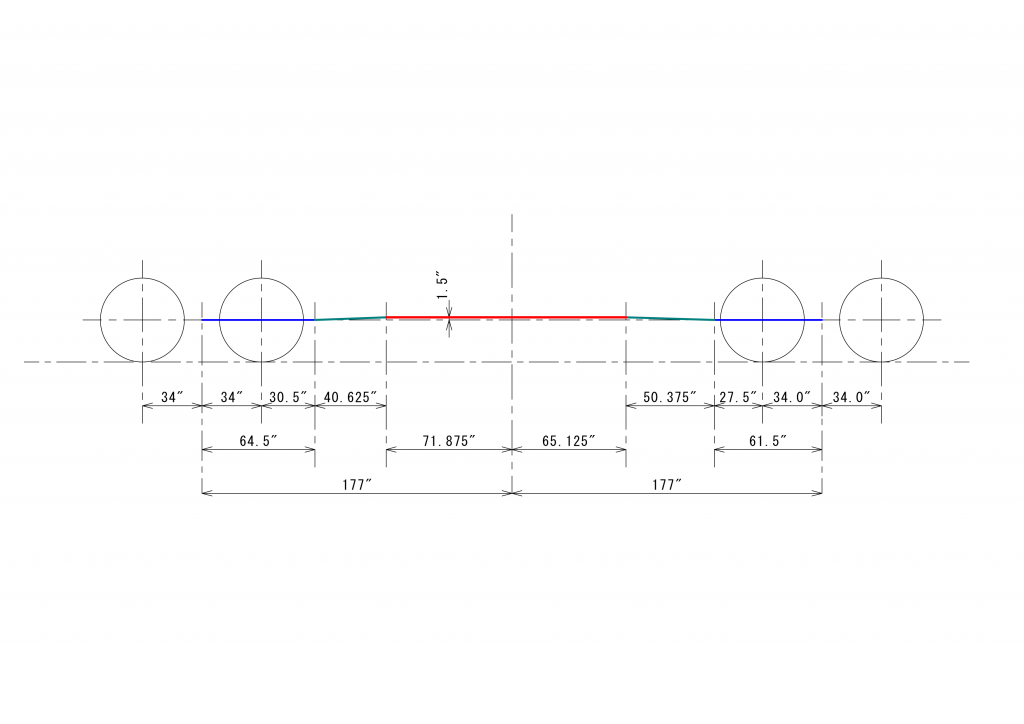
この150tのShayは、以前紹介したWestern MarylandのShayに匹敵する最大級のShayです。Western Marylandと同じく、最小半径は22度のであると仮定して議論を進めます。

まずは解析に必要な座標を計算します。駆動軸が平面にあるShayの座標の考え方に、上記の軸の高さを考慮したものが次のようになります。なお、これまでは駆動軸がカーブの内側にある場合と外側にある場合との両方を考えてきましたが、今回は条件の厳しい、カーブの内側にある場合のみを考慮することとします。

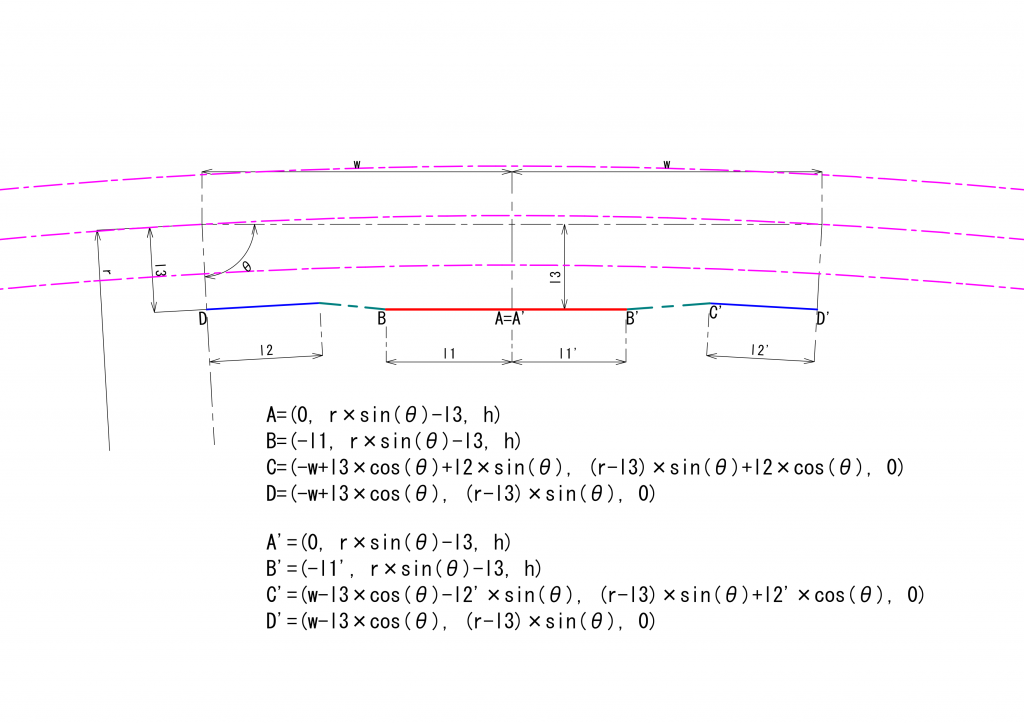
エンジンに向かって左側のユニバーサルジョイントの角速度の解析に必要な座標は、\(\theta=cos^{-1}(\frac{w}{r})\)とすると、

\(A=(0, -r\cdot sin(\theta)-{l_3}, h)\)

\(B=(-{l_1}, r\cdot sin(\theta)-{l_3}, h)\)

\(C=(-w+{l_3}\cdot cos(\theta)+{l_2}\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}\cdot cos(\theta),0)\)

\(D=(-w+{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)

となります。

求める角速度比を得るには、\(\vec{AB}\)と\(\vec{BC}\)とのなす角\(\alpha\)、\(\vec{BC}\)と\(\vec{CD}\)とのなす角\(\beta\)、\(\vec{AB}\)と\(\vec{BC}\)との外積\(\vec{AB}\times\vec{BC}\)に対して\(\vec{BC}\)と\(\vec{CD}\)との外積\(\vec{BC}\times\vec{CD}\)がどれだけ回転してるかの角度\(\eta\)を求め、

\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)

を計算します。

Shayの場合は、エンジンの左側と右側とで寸法が異なることが大半ですので、右側の角速度比は左側と同様の計算方法で別途求める必要があります。まずはエンジンに向かって右側のユニバーサルジョイントの解析に必要な座標は、

\(A’=(0, -r\cdot sin(\theta)-{l_3}, h)\)

\(B’=(-{l_1}’, r\cdot sin(\theta)-{l_3}, h)\)

\(C’=(w-{l_3}\cdot cos(\theta)-{l_2}’\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}’\cdot cos(\theta),0)\)

\(D’=(w-{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)

となります。

これの座標から、\(\vec{A’B’}\)と\(\vec{B’C’}\)とのなす角\(\alpha’\)、\(\vec{B’C’}\)と\(\vec{C’D’}\)とのなす角\(\beta’\)、\(\vec{A’B’}\)と\(\vec{B’C’}\)との外積\(\vec{A’B’}\times\vec{B’C’}\)に対して\(\vec{B’C’}\)と\(\vec{C’D’}\)との外積\(\vec{B’C’}\times\vec{C’D’}\)がどれだけ回転してるかの角度\(\eta’\)を求めます。

前回触れたように、エンジンの左側の角速度を\(\omega\)とした場合、右側の角速度は\(-\omega\)となりますので、求める角速度比は

\(\frac{cos(\alpha’)\cdot cos(\beta’) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha’) – (cos(\omega t)\cdot cos(\delta-\eta’)+sin(\omega t)\cdot cos(\alpha’)\cdot sin(\delta-\eta’))^2\cdot{sin}^2(\beta’)}\)

となります。

得られた計算式で、位相が正しい場合と、位相が間違っている場合との角速度の変動を計算した結果を次のグラフに示します。

比較のために、エンジンの中心軸が、台車の軸と水平になった(h=0)場合のグラフと重ねてみたものを示します。

これで見る限り、h=1.5”としても、1%を下回る角速度の変動となりますので、実用上は大きくは影響を与えないであろうということは言えるかと思います。少しでも高さを稼ぎたい理由があったのでしょうか。

いまさら言わなくても、という気がしますが、逆位相の場合に急激に変動が大きくなる傾向は、MPギアの時の計算結果と同じとなります。