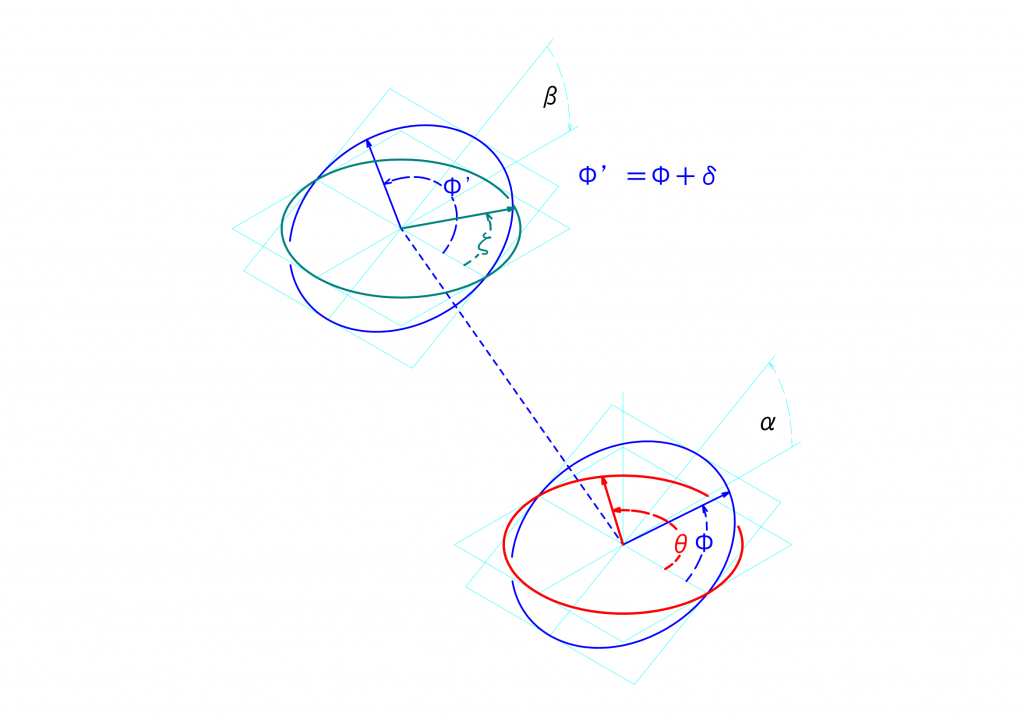
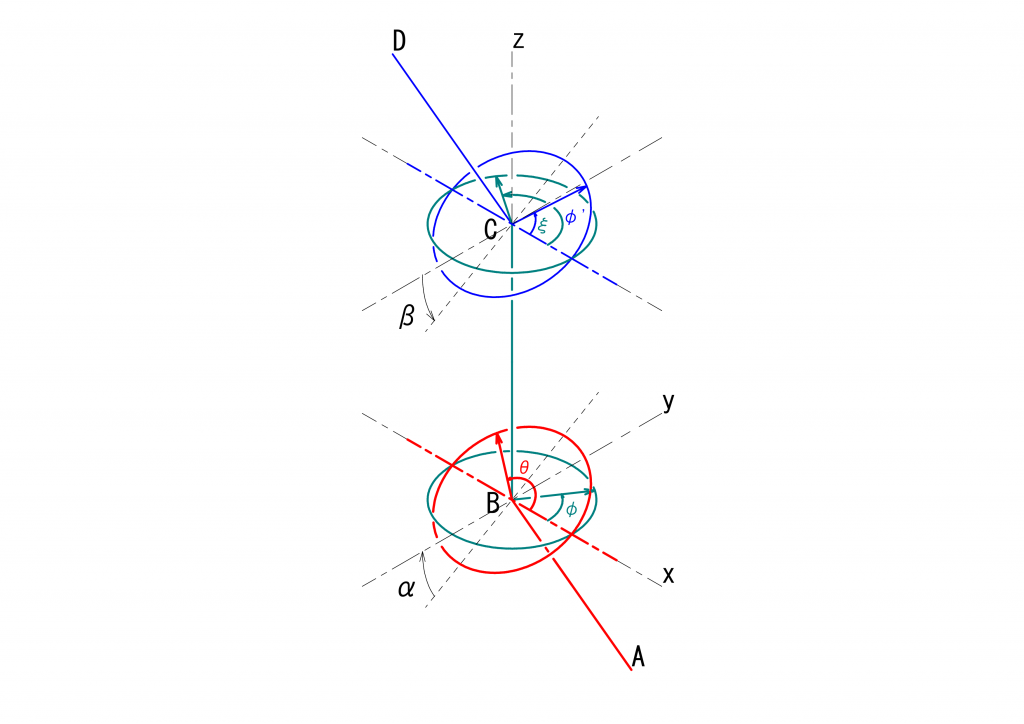
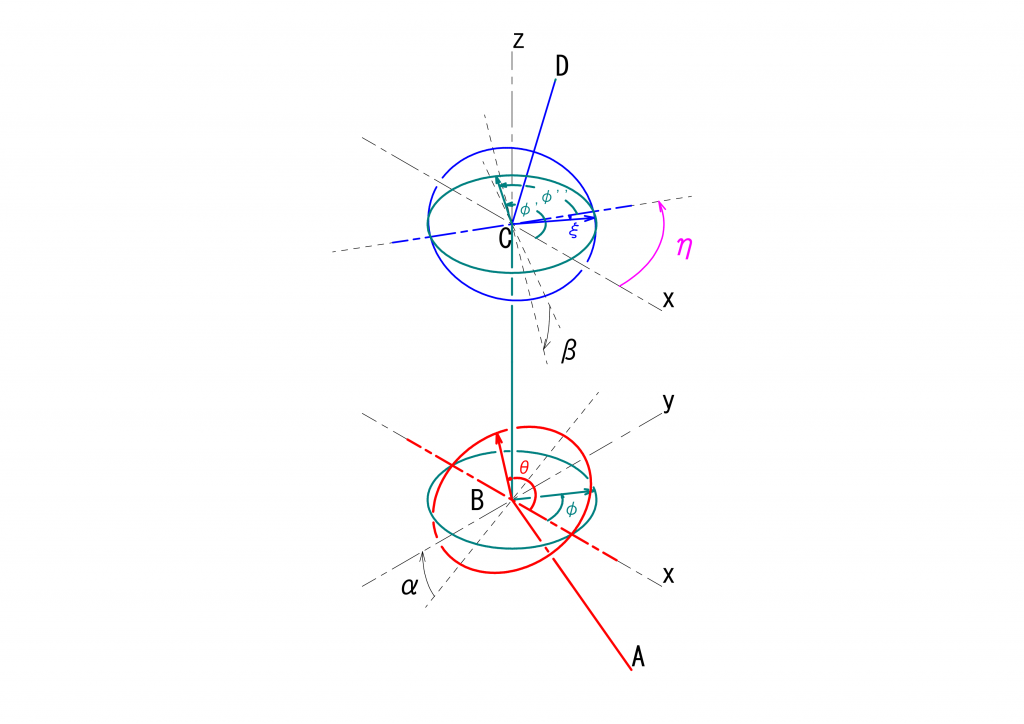
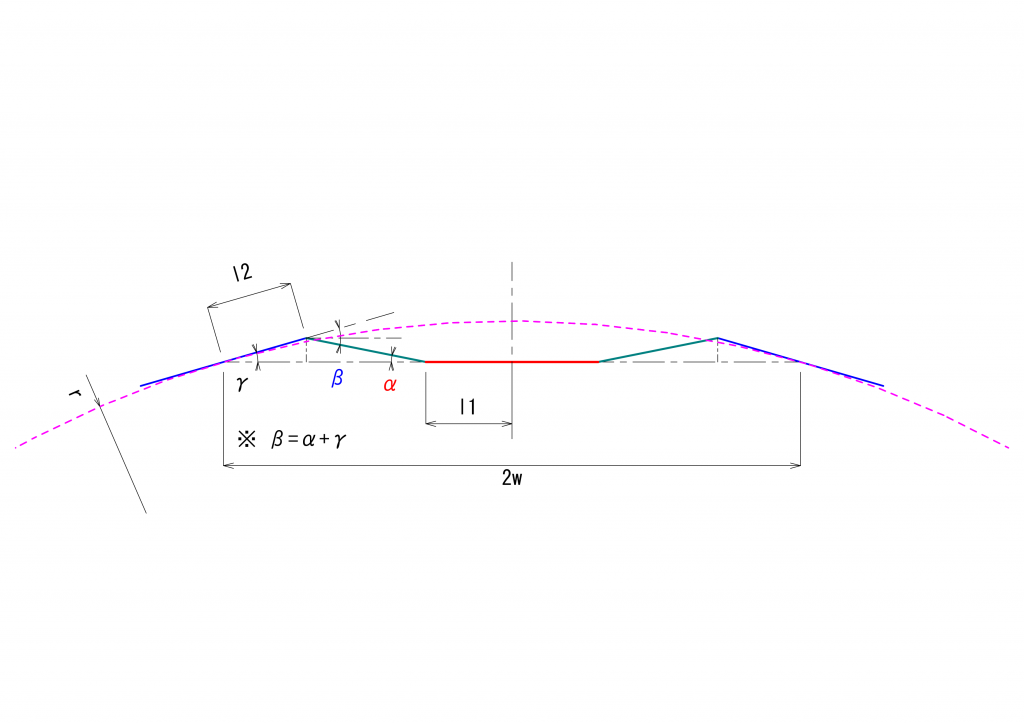
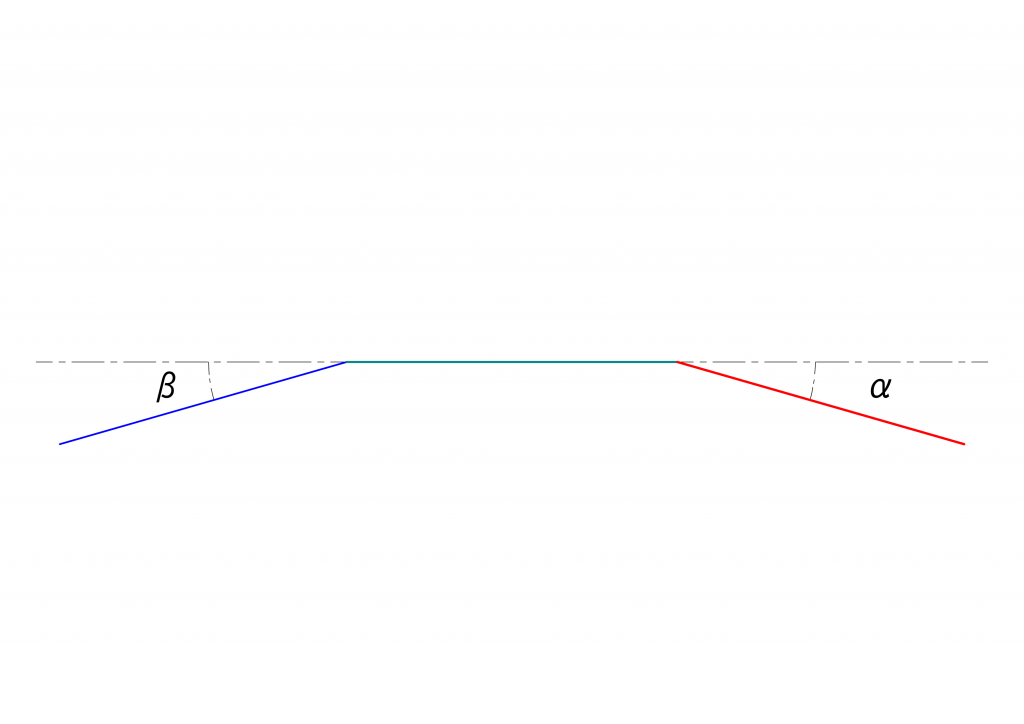
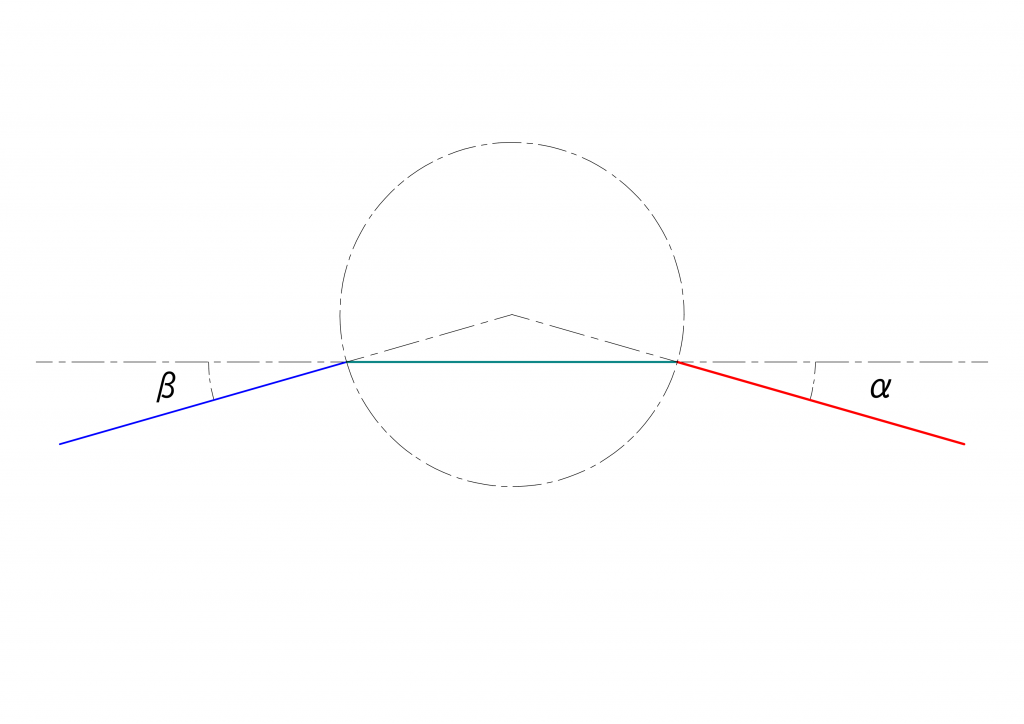
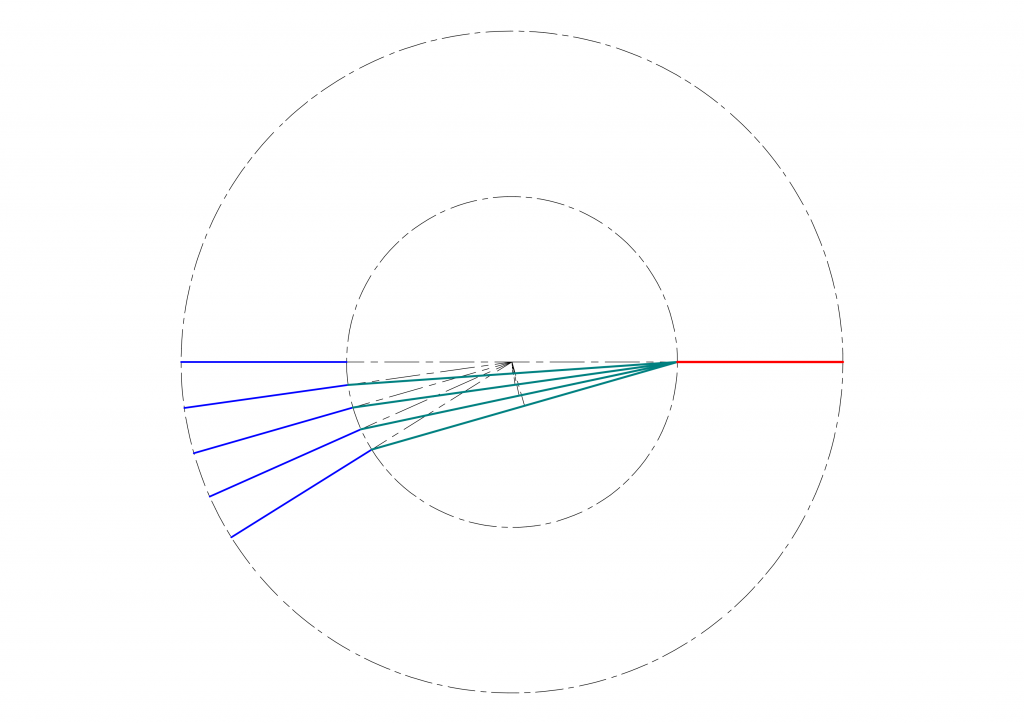
2つのユニバーサルジョイントを組み合わせたときに、最終伝達面の基準点の角度\(\xi\)は、駆動面の駆動点の角度\(\theta = \omega t\)を用いて次の式となるのでした。
\(\xi=tan^{-1}(\frac{sin(\delta)+tan(\omega t)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta) – tan(\omega t)\cdot sin(\delta)\cdot cos(\alpha)}\cdot\frac{1}{cos(\beta)})\)
これを\(t\)について微分すれば、最終伝達面の基準点の角速度を求めることができます。
見通し良く計算するために、
\(f(t)=sin(\delta) + tan(\omega t)\cdot cos(\delta)\cdot cos(\alpha)\)
\(g(t)=cos(\delta) – tan(\omega t)\cdot sin(\delta)\cdot cos(\alpha)\)
\(u(t)= \frac{f(t)}{g(t)}\cdot\frac{1}{cos(\beta)}\)
とします。すると、
\(\frac{d\xi}{dt} = \frac{d}{dt}(tan^{-1}(u(t)))= \frac{1}{1+u^2(t)}\cdot\frac{du(t)}{dt}\)
\(= \frac{1}{1 +(\frac{f(t)}{g(t)}\cdot\frac{1}{cos(\beta)})^2}\cdot \frac{du(t)}{dt}=\frac{g^2(t)\cdot cos^2(\beta)}{g^2(t)\cdot cos^2(\beta) + f^2(t)} \cdot \frac{du(t)}{dt}\)
関数の商の微分の公式は\(\frac{d}{dx}(\frac{f(x)}{g(x)})=\frac{\frac{d}{dx}(f(x))\cdot g(x) – f(x)\cdot\frac{d}{dx}(g(x))}{g^2(x)}\)ですので、
\(\frac{du(t)}{dt}=\frac{d}{dt}(\frac{f(t)}{g(t)}\cdot\frac{1}{cos(\beta)}) = \frac{1}{cos(\beta)}\cdot \frac{\frac{d}{dt}(f(t))\cdot g(t) – f(t)\cdot\frac{d}{dt}(g(t))}{g^2(t)}\)
ここまでを整理すると、
\(\frac{d\xi}{dt} = \frac{g^2(t)\cdot cos^2(\beta)}{g^2(t)\cdot cos^2(\beta) + f^2(t)}\cdot \frac{1}{cos(\beta)}\cdot \frac{\frac{d}{dt}(f(t))\cdot g(t) – f(t)\cdot\frac{d}{dt}(g(t))}{g^2(t)}\)
\(=cos(\beta)\cdot \frac{\frac{d}{dt}(f(t))\cdot g(t) – f(t)\cdot\frac{d}{dt}(g(t))}{g^2(t)\cdot cos^2(\beta) + f^2(t)}\)
となります。
ここで、\(\frac{d}{dt}(f(t))\)、\(\frac{d}{dt}(g(t))\)は、それぞれ
\(\frac{d}{dt}(f(t)) = \frac{d}{dt}(sin(\delta)+tan(\omega t)\cdot cos(\delta)\cdot cos(\alpha))=\frac{\omega}{cos^2(\omega t)}\cdot cos(\delta)\cdot cos(\alpha)\)
\(\frac{d}{dt}(g(t)) = \frac{d}{dt}(cos(\delta) – tan(\omega t)\cdot sin(\delta)\cdot cos(\alpha))=-\frac{\omega}{cos^2(\omega t)}\cdot sin(\delta)\cdot cos(\alpha)\)
となります。従って、
\(\frac{d}{dt}(f(t))\cdot g(t) – f(t)\cdot\frac{d}{dt}(g(t)) =\)
\(\frac{\omega}{cos^2(\omega t)}\cdot((cos(\delta)\cdot cos(\alpha)\cdot(cos(\delta) – tan(\omega t)\cdot sin(\delta)\cdot cos(\alpha))\)
\(- (sin(\delta)+tan(\omega t)\cdot cos(\delta)\cdot cos(\alpha))\cdot -sin(\delta)\cdot cos(\alpha)))\)
\(= \frac{\omega}{cos^2(\omega t)}\cdot cos(\alpha) \cdot(cos^2(\delta) – sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\cdot tan(\omega t) \)
\(+ sin^2(\delta) + sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\cdot tan(\omega t))\)
\(= \frac{\omega}{cos^2(\omega t)}\cdot cos(\alpha)\cdot (sin^2(\delta)+cos^2(\delta))\)
\(sin^2(x)+cos^2(x)=1\)を利用すると、
\(\frac{d}{dt}(f(t))\cdot g(t) – f(t)\cdot\frac{d}{dt}(g(t)) = \frac{\omega}{cos^2(\omega t)}\cdot cos(\alpha)\)
を得ます。
次に\(g^2(t)\cdot cos^2(\beta) + f^2(t)\)を計算します。
\(g^2(t)\cdot cos^2(\beta) + f^2(t)\)
\(=(cos(\delta) – tan(\omega t)\cdot sin(\delta)\cdot cos(\alpha))^2\cdot cos^2(\beta) \)
\(+ (sin(\delta)+tan(\omega t)\cdot cos(\delta)\cdot cos(\alpha))^2\)
\(=cos^2(\delta)\cdot cos^2(\beta)-2\cdot tan(\omega t)\cdot sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\cdot cos^2(\beta)\)
\(+ tan^2(\omega t) \cdot sin^2(\delta) \cdot cos^2(\alpha)\cdot cos^2(\beta) \)
\(+ sin^2(\delta)+2\cdot tan(\omega t)\cdot sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\)
\(+ tan^2(\omega t)\cdot cos^2(\delta)\cdot cos^2(\alpha)\)
\(=cos^2(\delta)\cdot cos^2(\beta) + sin^2(\delta)\)
\(+2\cdot tan(\omega t)\cdot sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\cdot (1 – cos^2(\beta))\)
\(+ tan^2(\omega t) \cdot cos^2(\alpha)\cdot(sin^2(\delta) \cdot cos^2(\beta) + cos^2(\delta))\)
\(sin^2(x)+cos^2(x)=1\)を利用すると、
\(g^2(t)\cdot cos^2(\beta)+f^2(t)=\)
\((1-cos^2(\delta)\cdot sin^2(\beta))\)
\(+2\cdot tan(\omega t)\cdot sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)\cdot sin^2(\beta)\)
\(+tan^2(\omega t)\cdot cos^2(\alpha)\cdot (1- sin^2(\delta)\cdot sin^2(\beta))\)
\(= 1 + tan^2(\omega t)\cdot cos^2(\alpha) – \)
\((tan^2(\omega t)\cdot cos^2(\alpha)\cdot sin^2(\delta)-2\cdot tan(\omega t)\cdot sin(\delta)\cdot cos(\delta)\cdot cos(\alpha)+cos^2(\delta))\cdot sin^2(\beta)\)
\(= 1+tan^2(\omega t)\cdot {cos}^2(\alpha) – (tan(\omega t)\cdot cos(\alpha)\cdot sin(\delta)-cos(\delta))^2\cdot{sin}^2(\beta)\)
となります。
ここまでの結果をまとめると
\(\frac{d\xi}{dt} = cos(\beta)\cdot \frac{\frac{\omega}{cos^2(\omega t)}\cdot cos(\alpha)}{1+tan^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\delta)-tan(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
\(= \frac{\omega\cdot cos(\alpha)\cdot cos(\beta) }{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
我々の興味があるのは、\(\delta=0\)の場合と、\(\delta=\frac{\pi}{2}\)の場合です。
\(\delta=0\)の場合は、\(sin(\delta)=0\)、\(cos(\delta)=1\)なので
\(\frac{d\xi}{dt}=\frac{\omega \cdot cos(\alpha) \cdot cos(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha) – cos^2(\omega t)\cdot sin^2(\beta)}\)
\(=\frac{\omega \cdot cos(\alpha) \cdot cos(\beta)}{cos^2(\omega t)\cdot(1-sin^2(\beta))+sin^2(\omega t)\cdot cos^2(\alpha)}\)
\(=\frac{\omega \cdot cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)\cdot cos^2(\beta) + sin^2(\omega t)\cdot cos^2(\alpha)}\)
\(|\alpha| = |\beta|\)とすると、
\(\frac{d\xi}{dt}=\frac{\omega \cdot cos^2(\alpha)}{cos^2(\omega t)\cdot cos^2(\alpha)+sin^2(\omega t)\cdot cos^2(\alpha)}\)
\(=\frac{\omega \cdot cos^2(\alpha)}{(cos^2(\omega t) + sin^2(\omega t))\cdot cos^2(\alpha)}= \omega\)
となり、駆動面と最終伝達面の角速度とが等しいことが確認できました。
\(\delta=\frac{\pi}{2}\)の場合は、\(sin(\delta)=1\)、\(cos(\delta)=0\)なので、
\(\frac{d\xi}{dt}=\frac{\omega\cdot cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha)- sin^2(\omega t)\cdot cos^2(\alpha)\cdot sin^2(\beta)}\)
\(=\frac{\omega\cdot cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha)\cdot(1-sin^2(\beta))}\)
\(=\frac{\omega\cdot cos(\alpha)\cdot cos(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha)\cdot cos^2(\beta)}\)
仮に\(|\alpha| = |\beta|\)とすると、
\(\frac{d\xi}{dt}=\frac{\omega\cdot cos^2(\alpha)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^4(\alpha)}\)
となります。前回の議論で得たユニバーサルジョイント1つの場合の伝達面の基準点の角速度の式
\(\frac{d\varphi}{dt}=\frac{\omega\cdot cos(\alpha)}{cos^2(\omega t)+sin^2(\omega t)\cdot cos^2(\alpha)}\)
によく似た形になりますが、\(cos(\alpha)\)の次数が異なります。
かなり乱暴に言うと、ユニバサールジョイント1つの場合は、\(\frac{1}{cos(\alpha)}\)に応じて角速度が変化するの対し、ユニバーサルジョイント2つを位相を90度ずらして繋いだ場合は、\(\frac{1}{cos^2(\alpha)}\)に応じて角速度が変化する(角速度の変化が拡大される)、ということが言えるかと思います。