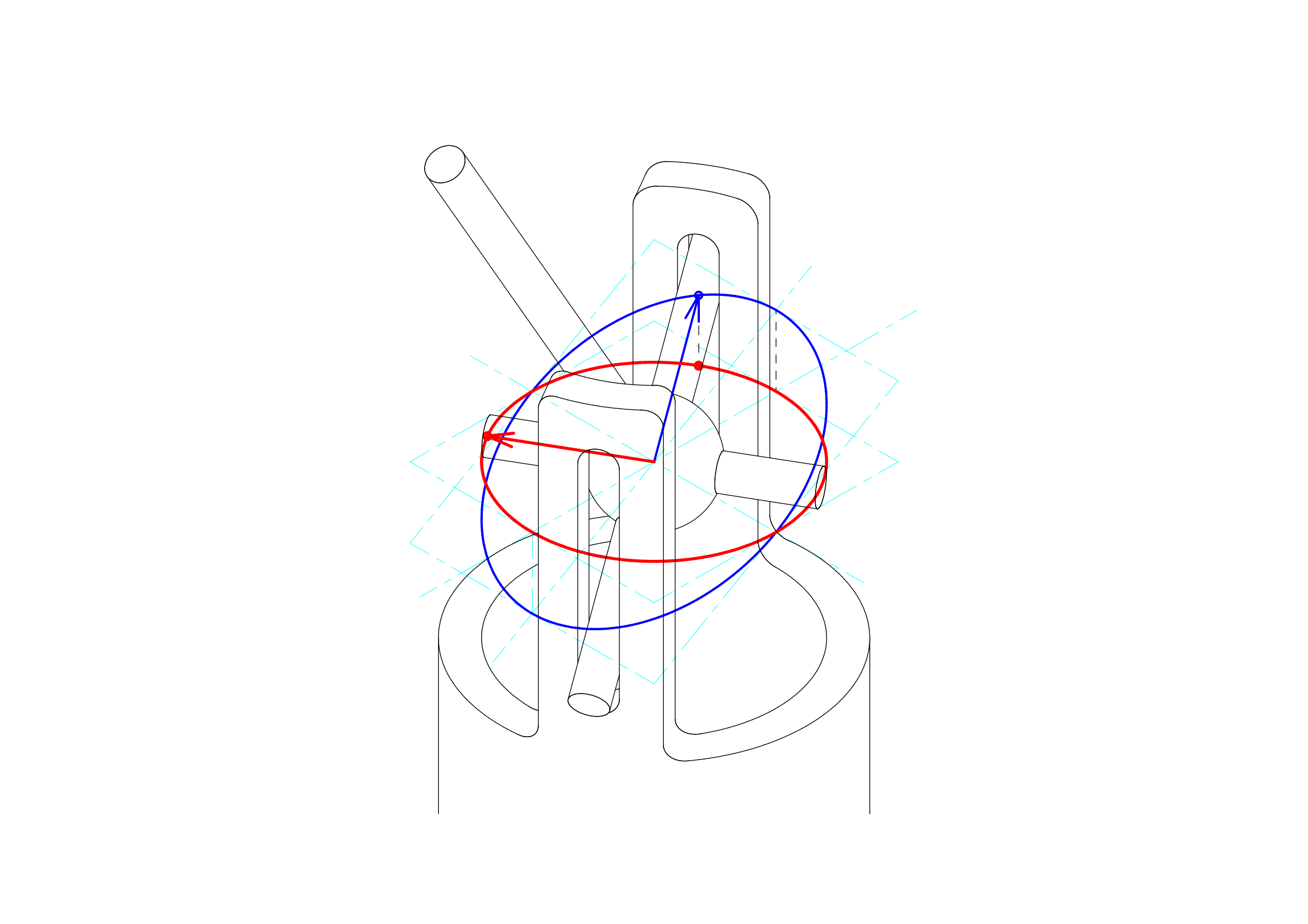
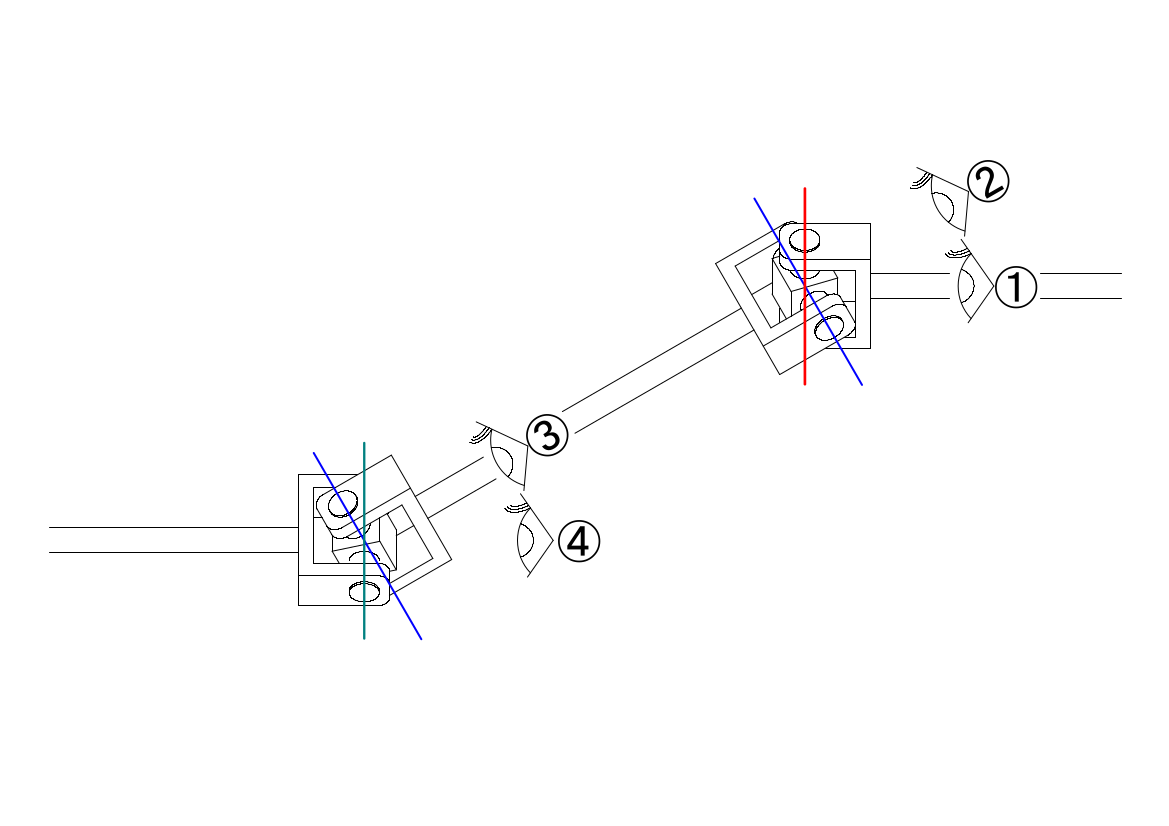
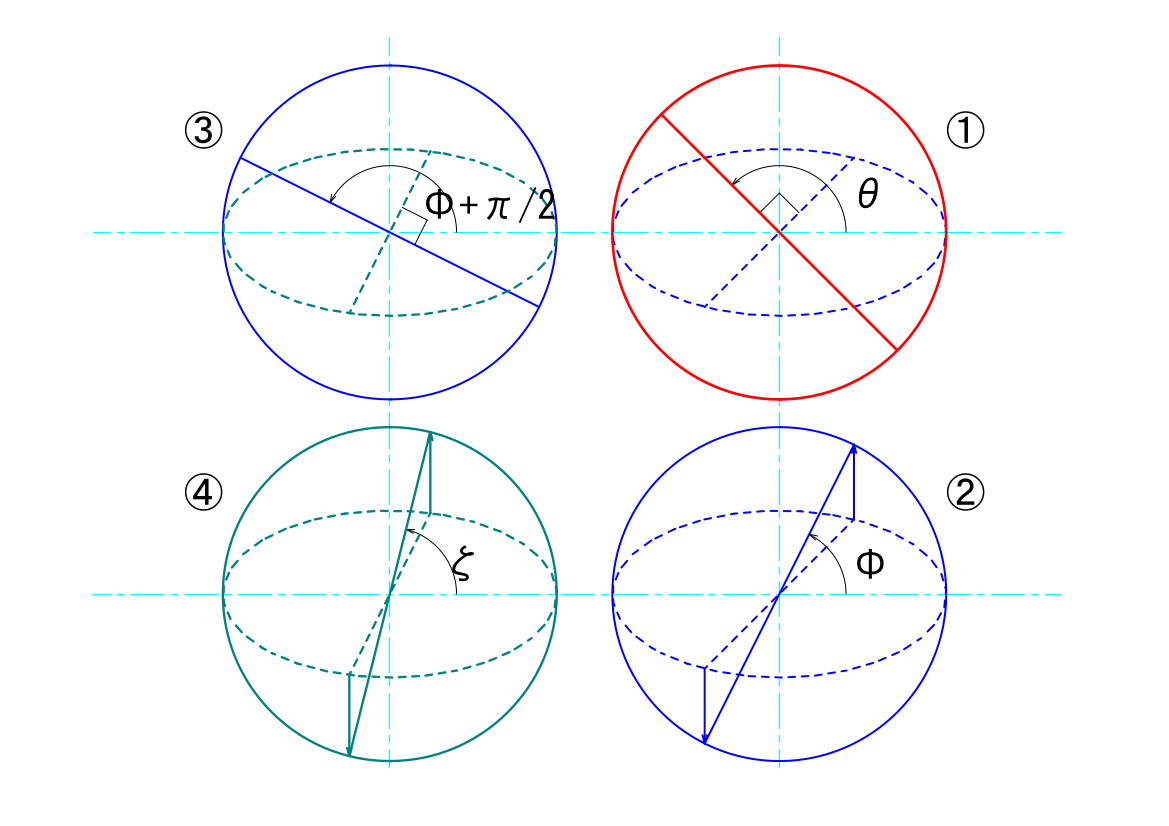
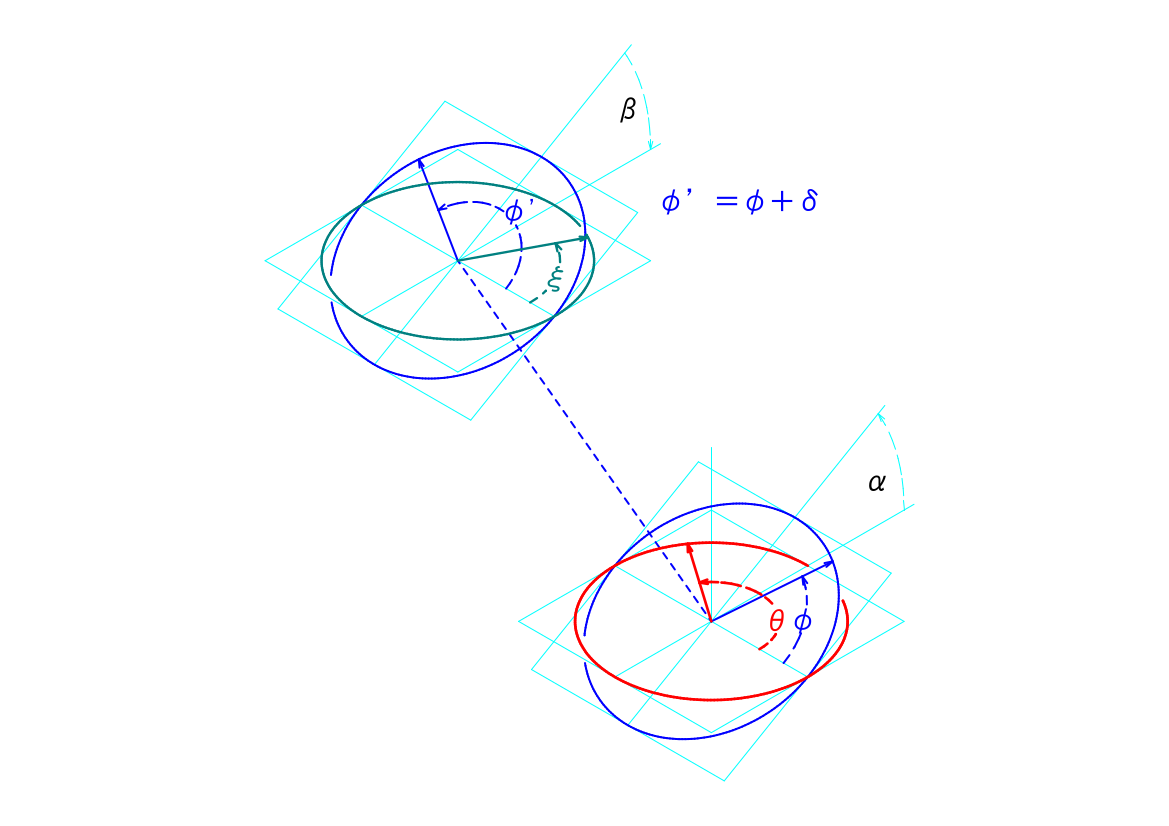
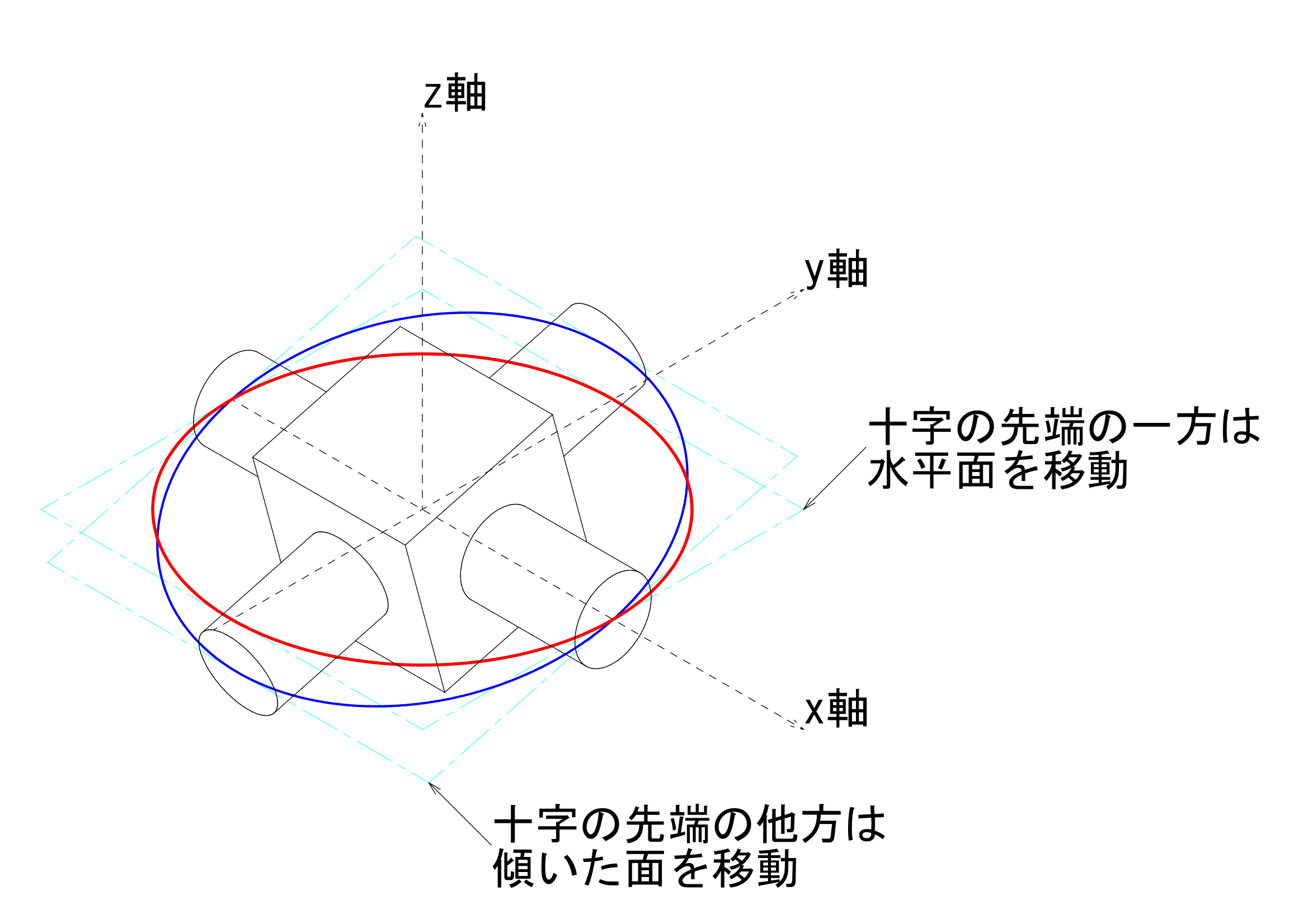
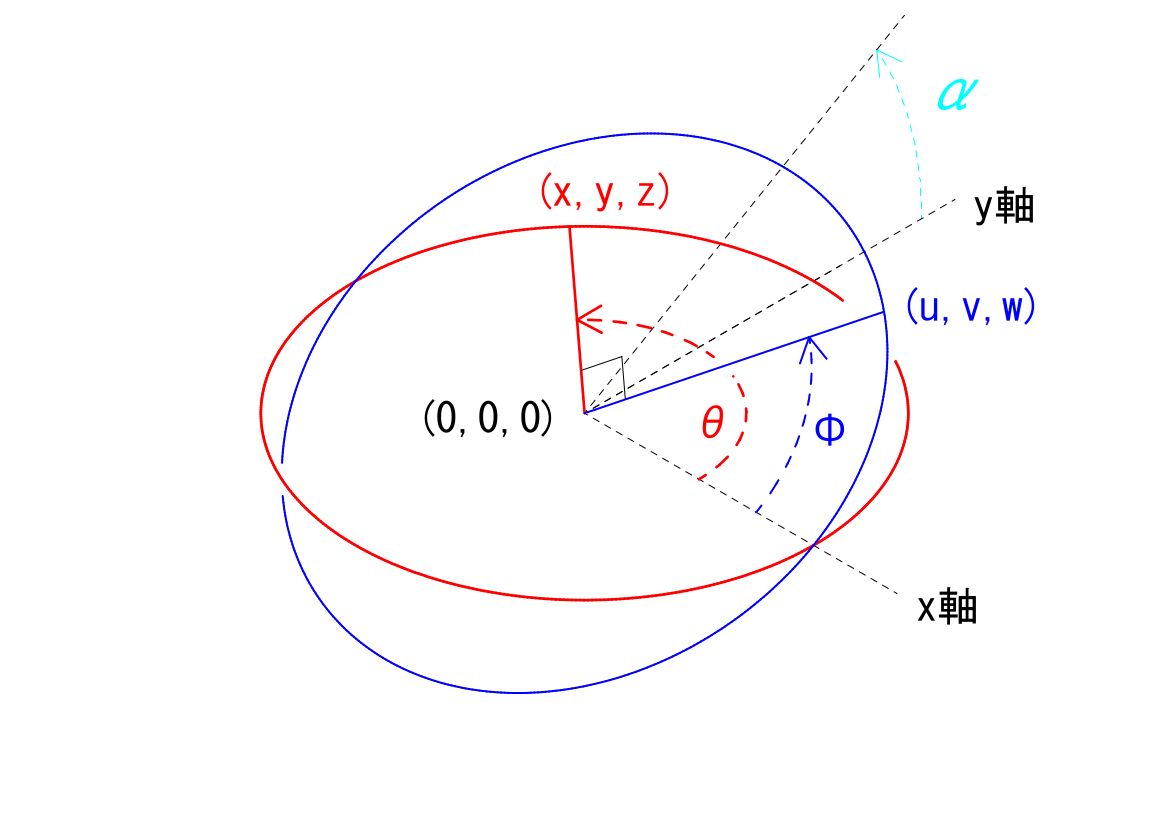
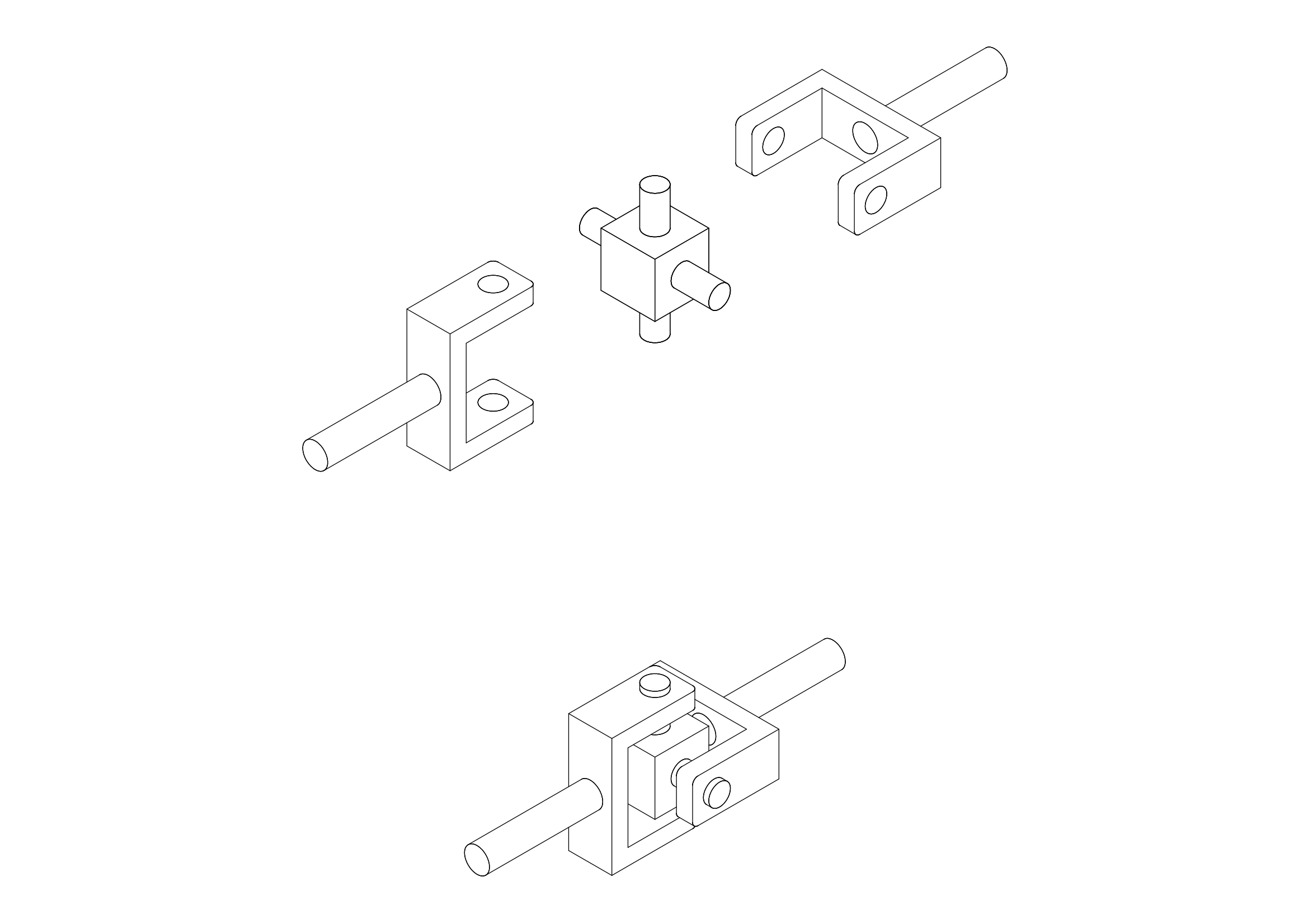
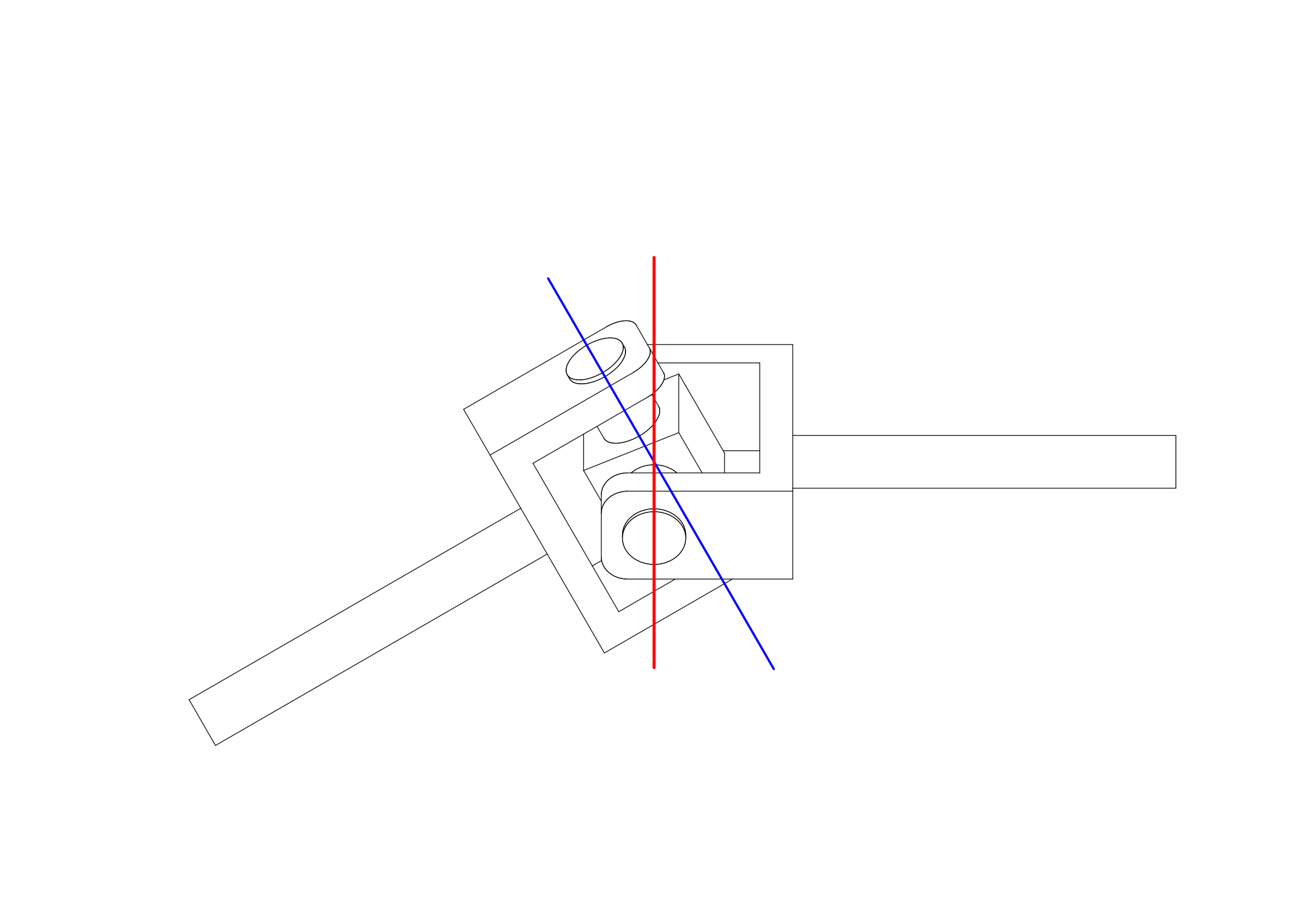
もともは、「ユニバーサルジョイントを正しく使わないと、動力側と伝達した側とで角速度が異なる」ということからスタートしましたので、ここでは角速度の式を導出してみたいと思います。角速度は、時間によって変化する角度を時間で微分すれば得ることができます。これも高校１年生で学習する範囲かと思います。

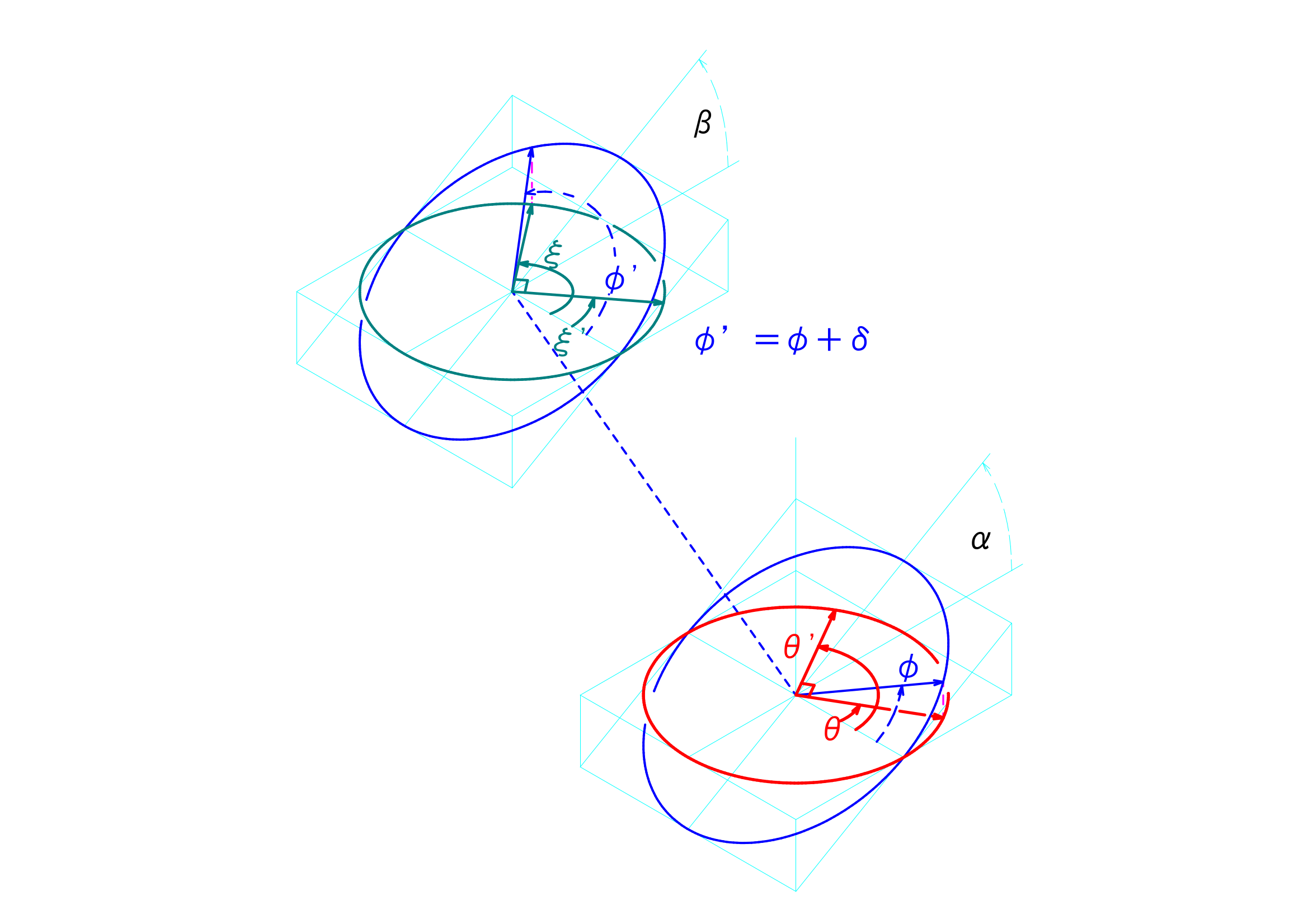
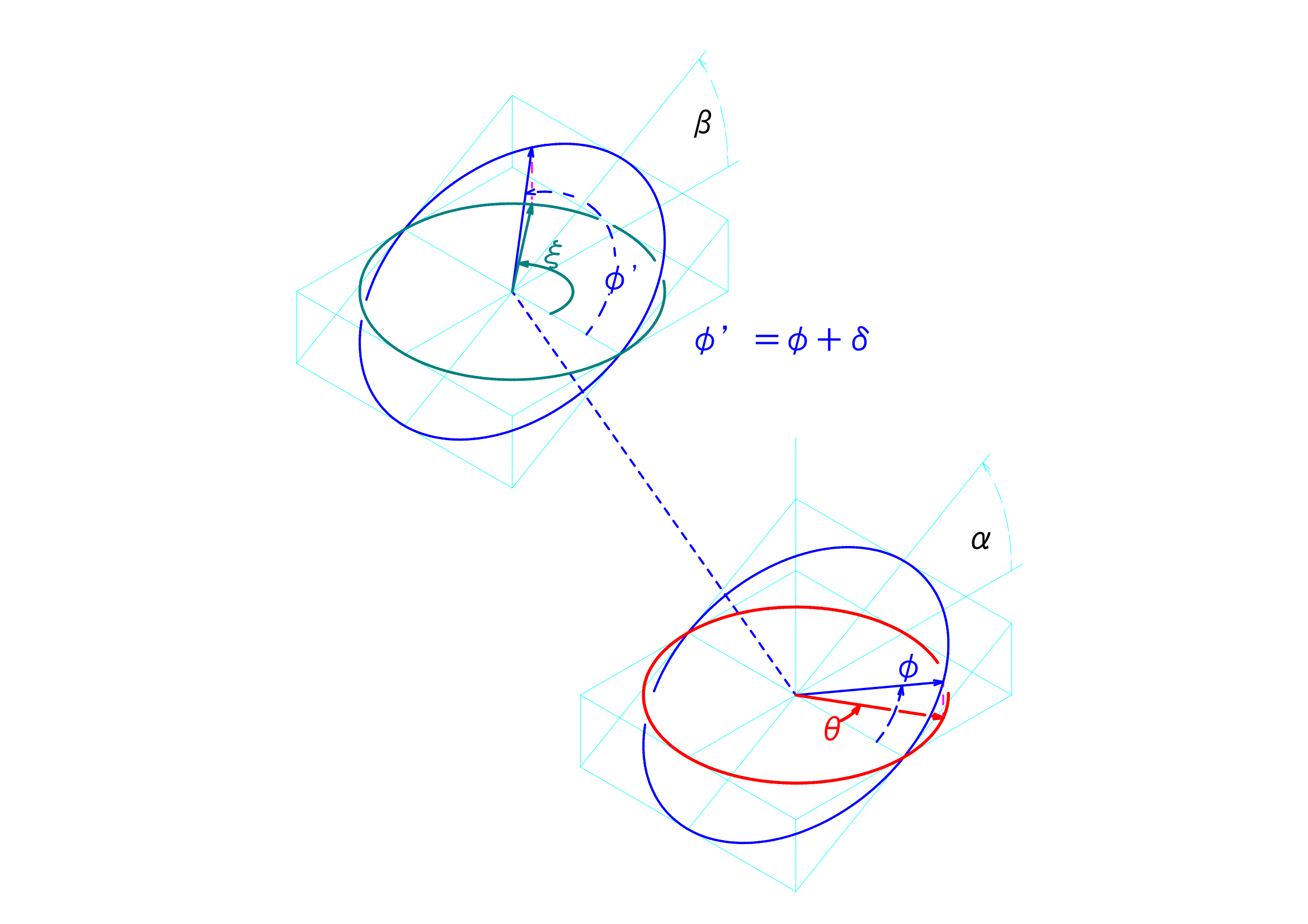
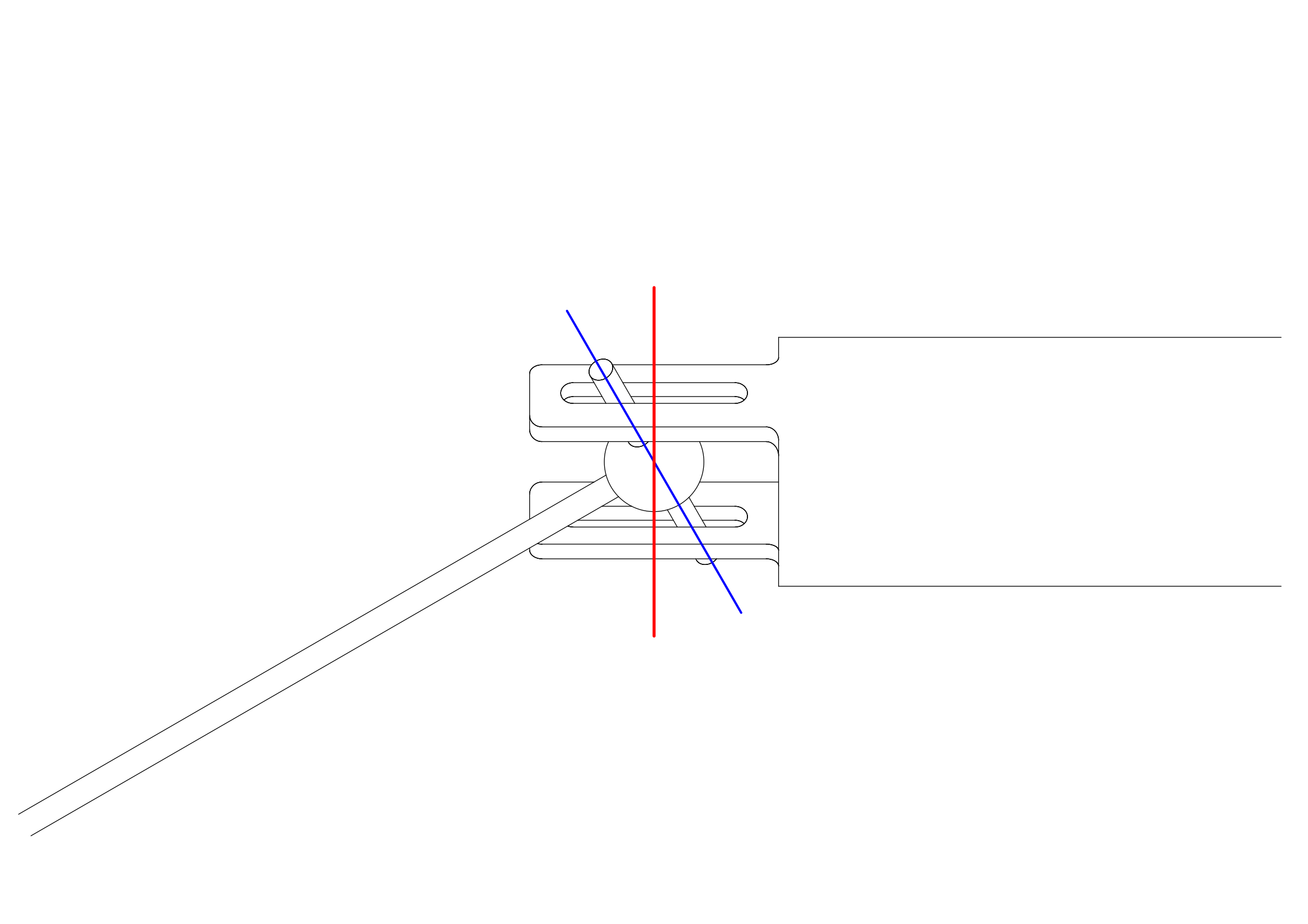
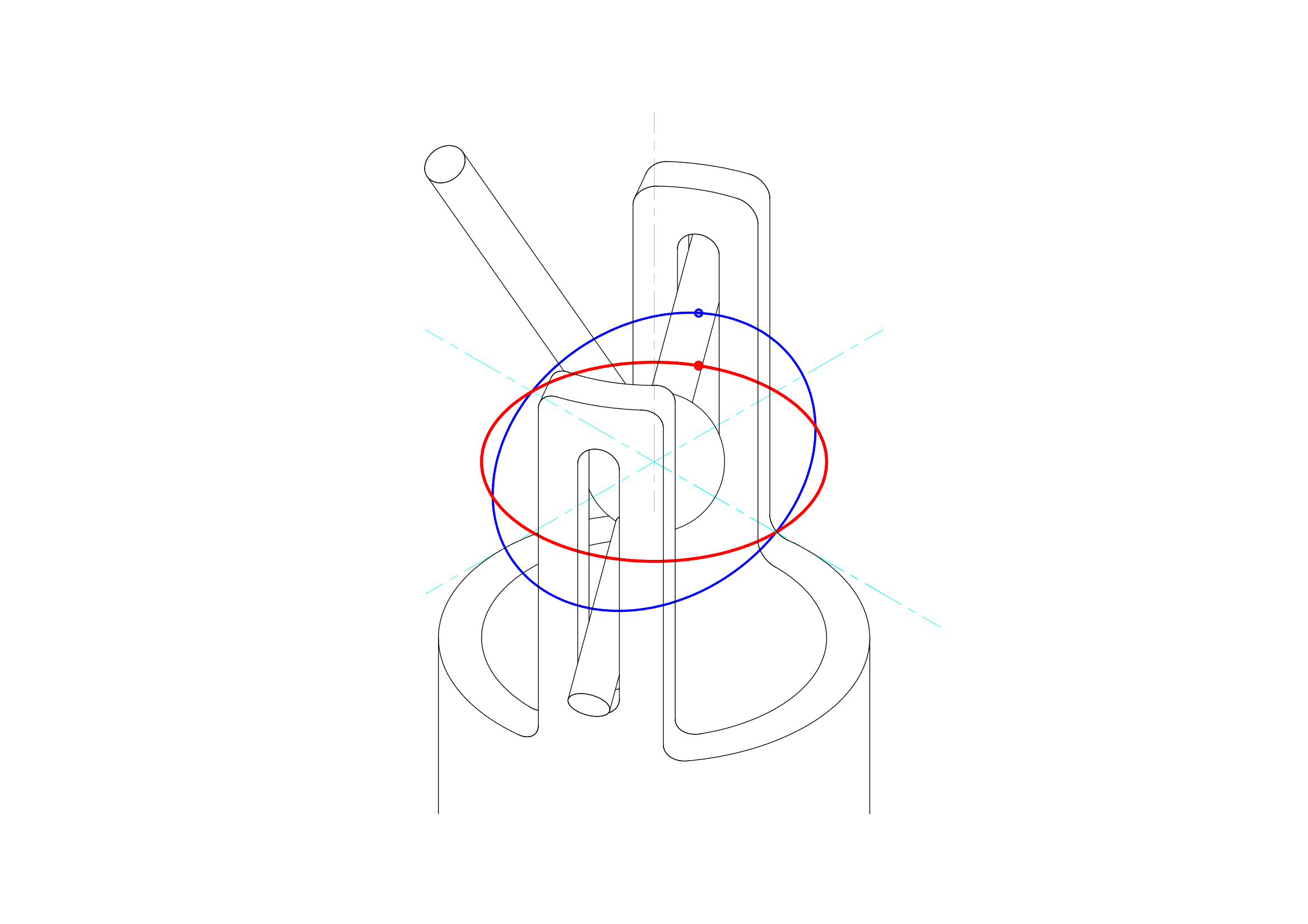
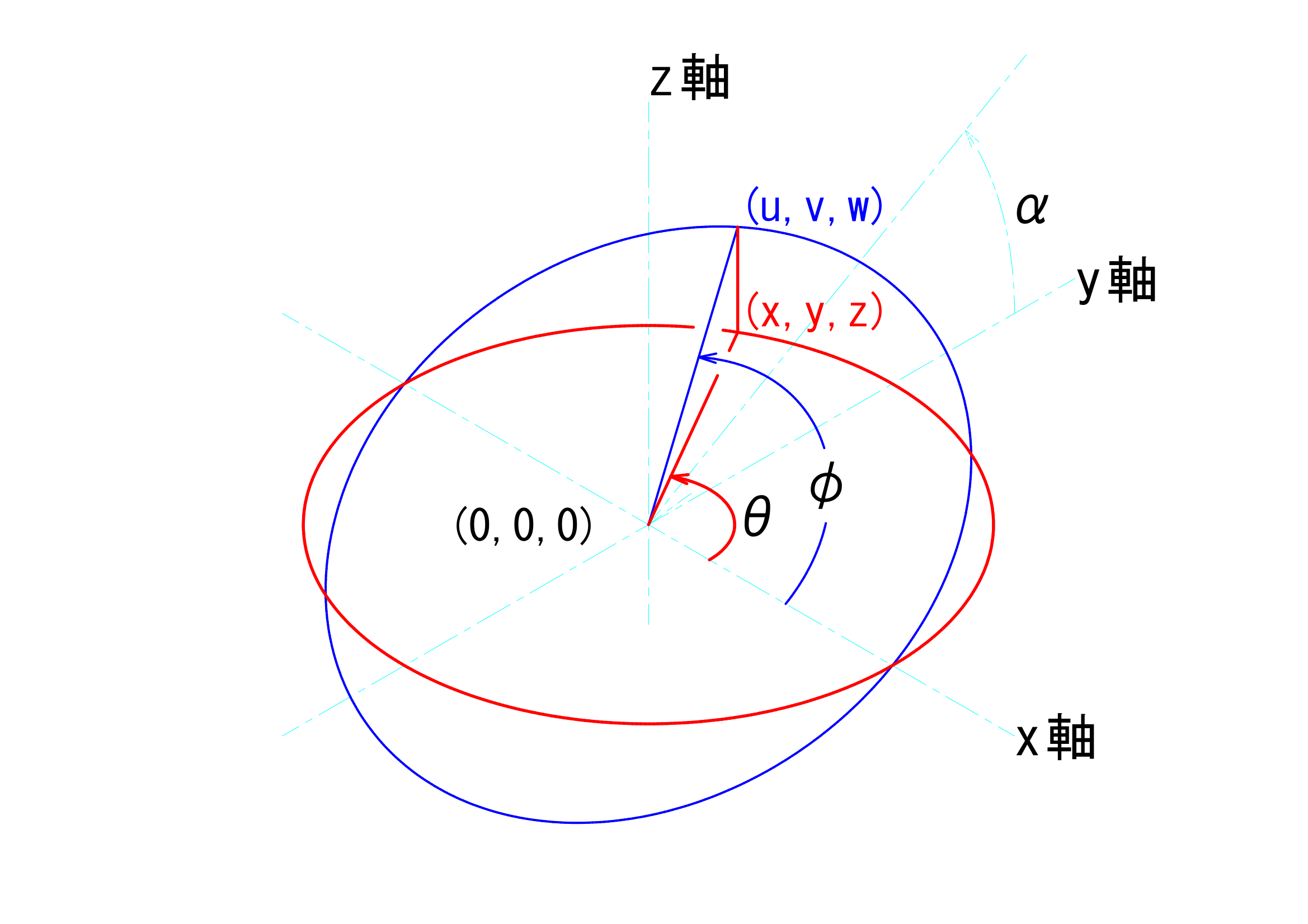
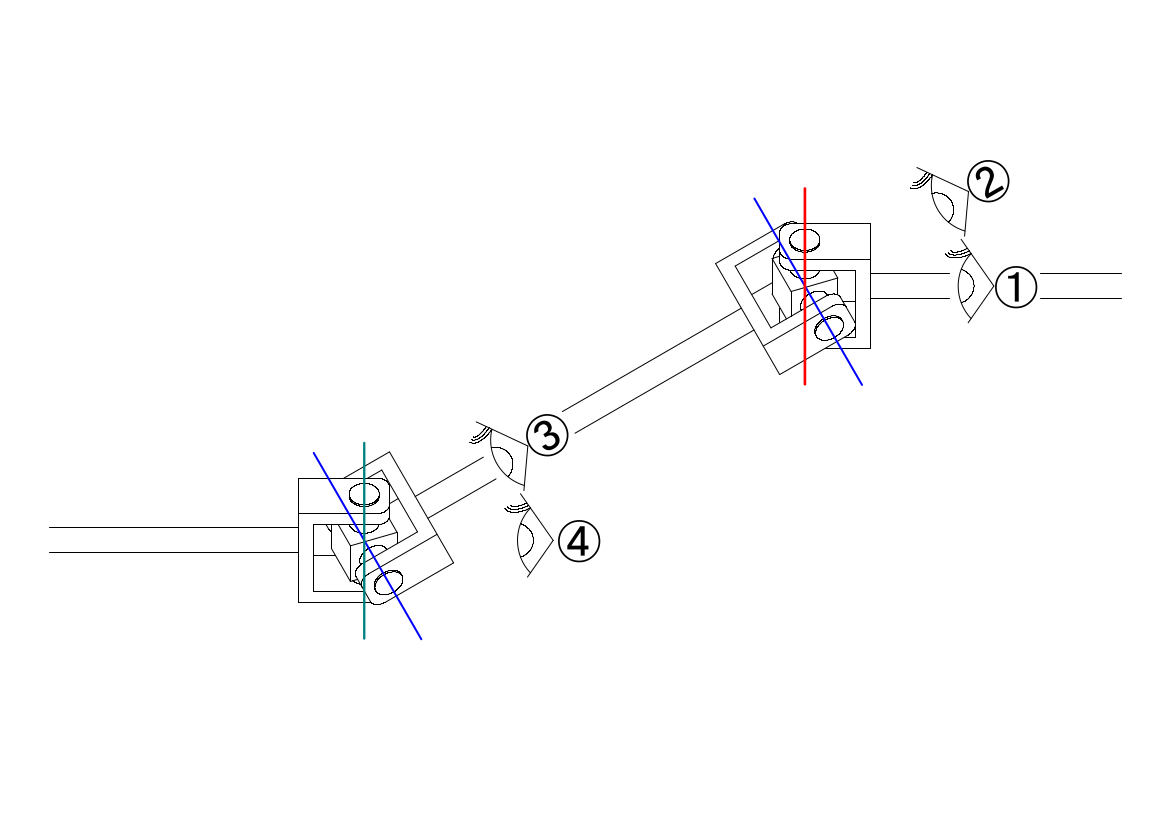
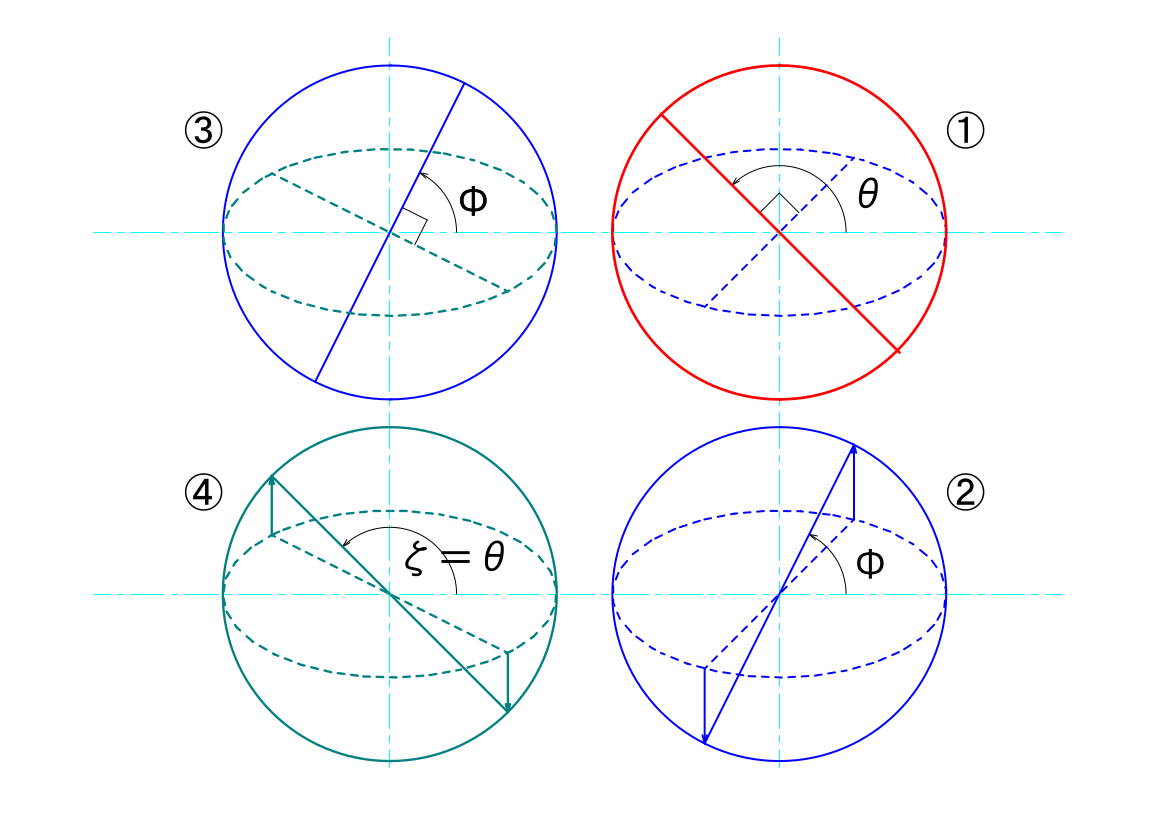
ユニバーサルジョイントの駆動面と伝達面との基準点との関係は、以下のようにあらわすことができるのでした。

\(\varphi=tan^{-1}(-\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\beta)})\)

駆動面の基準点の角速度を\(\omega\)とすると、\(\theta=\omega t\)となりますので、これを上の式に代入したものを\(t\)で微分すれば、伝達面の基準点の角速度を求めることができます。

\(\frac{d\varphi}{d t}= \frac{d}{dt}tan^{-1}(-\frac{1}{tan(\omega t)}\cdot\frac{1}{cos(\alpha)})\)

合成関数\(f(g(x))\)を\(x\)について微分するには、

\(\frac{d}{d x}(f(g(x))) = \frac{d f(u)}{d u}\cdot \frac{d g(x)}{d x}\)

を求めればよいので、\(u=-\frac{1}{tan(\omega t)}\cdot\frac{1}{cos(\alpha)}\)と置くと、

\(\frac{d \varphi}{d t} = \frac{d}{d u}(tan^{-1}(u))\cdot \frac{d}{d t}(-\frac{1}{tan(\omega t)}\cdot\frac{1}{cos(\alpha)})\)

となります。

\(\frac{d}{dx}(tan^{-1}(x))=\frac{1}{1+x^2}\)ですので、

\(\frac{d}{d u}(tan^{-1}(u)) = \frac{1}{1 + u^2} =  \frac{1}{1 + \frac{1}{tan^2(\omega t) \cdot cos^2 (\alpha)}}\)

\(=  \frac{1}{1 + \frac{cos^2(\omega t)}{sin^2(\omega t) \cdot cos^2 (\alpha)}} = \frac{sin^2(\omega t)\cdot cos^2(\alpha)}{cos^2(\omega t) + sin^2(\omega t)\cdot cos^2(\alpha)}\)

を得ます。

次に\(\frac{d}{d t}(-\frac{1}{tan(\omega t)}\cdot\frac{1}{cos(\alpha)})\)を計算します。\(\alpha\)が定数だったとき\(\frac{d}{dx}(\alpha \cdot f(x)) =\alpha\cdot \frac{df(x)}{dx}\)ですので、

\(\frac{d}{d t}(-\frac{1}{tan(\omega t)}\cdot\frac{1}{cos(\alpha)}) = -\frac{1}{cos(\alpha)}\cdot \frac{d}{dt}(\frac{1}{tan(\omega t)})\)

上述した合成関数の微分に加え、\(\frac{d}{dx}(\frac{1}{x}) = -\frac{1}{x^2}\)、\(\frac{d }{dx}(tan(x))= \frac{1}{cos^2(x)}\)を利用すると、

\(\frac{d}{dt}(\frac{1}{tan(\omega t)}) = -\frac{1}{tan^2(\omega t) }\cdot \frac{d}{dt}(tan(\omega t))\)

\(= -\frac{1}{tan^2(\omega t) }\cdot \frac{1}{cos^2(\omega t)} \cdot \frac{d(\omega t)}{dt}\)

\(= -\frac{cos^2(\omega t)}{sin^2(\omega t) }\cdot\frac{1}{cos^2(\omega t)} \cdot \omega \)

\(= -\frac{\omega}{sin^2(\omega t)}\)

を得ます。

ここまでの結果をまとめると、

\(\frac{d\varphi}{d t} = \frac{sin^2(\omega t)\cdot cos^2(\alpha)}{cos^2(\omega t) + sin^2(\omega t)\cdot cos^2(\alpha)} \cdot -\frac{1}{cos(\alpha)}\cdot -\frac{\omega}{sin^2(\omega t)}\)

最終的に

\(\frac{d\varphi}{d t} = \frac{\omega\cdot cos(\alpha)}{cos^2(\omega t) + cos^2(\alpha)\cdot sin^2(\omega t)}\)

という式を得ます。従って、駆動面の基準点の角速度\(\omega\)に対する伝達面の基準点の角速度の比は、

\(\frac{cos(\alpha)}{cos^2(\omega t) + cos^2(\alpha)\cdot sin^2(\omega t)}\)

となります。

\(sin^2(\alpha)+cos^2(\alpha) =1\)であったことを利用すると、

\(cos^2(\omega t) + cos^2(\alpha)\cdot sin^2(\omega t) \)

\(= cos^2(\omega t) + sin^2(\omega t)  – sin^2(\omega t) + cos^2(\alpha)\cdot sin^2(\omega t)\)

\(=  1  – sin^2(\omega t) (1 – cos^2(\alpha))\)

\(= 1- sin^2(\omega t)\cdot sin^2(\alpha)\)

と変形でき、上記の角速度の比は

\(\frac{cos(\alpha)}{1- sin^2(\omega t)\cdot sin^2(\alpha)}\)

と表現することも可能です。これがWikipedia等に掲載されている式となります。

 

 

さて、正規型ユニバーサルジョイントを２つ組み合わせたときの\(\theta\)と\(\xi\)との関係は、

\(tan(\xi)=\frac{sin(\delta)+tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta)-tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

で、簡易型ユニバーサルジョイントを２つ組みわ合わせたときの\(\theta\)と\(\xi\)との関係は、

\(tan(\xi) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta)\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\cdot cos(\beta)\)

で表現されるのでした。

２つの式は似ているようで異なりますが、これはどういうことを意味しているのでしょうか。

簡易型ユニバーサルジョイントを２つ組み合わせたときの式に、\(\theta = \theta^\prime  – \frac{\pi}{2}\)、\(\xi = \xi^\prime + \frac{\pi}{2}\)、を代入して変形します。

\(tan(\xi^\prime + \frac{\pi}{2}) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta^\prime – \frac{\pi}{2})\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta^\prime  – \frac{\pi}{2})\cdot sin(\delta)}\cdot cos(\beta)\)

\(tan(\theta +\frac{\pi}{2}) = tan(\theta -\frac{\pi}{2}) = -\frac{1}{tan(\theta)}\)ですので、上記の式は

\(-\frac{1}{tan(\xi^\prime)} = \frac{sin(\delta)\cdot cos(\alpha) -\frac{1}{tan(\theta^\prime)}\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)+\frac{1}{tan(\theta^\prime)}\cdot sin(\delta)}\cdot cos(\beta)\)

となり、これを\(tan(\xi^\prime)\)について変形します。

\(tan(\xi^\prime) = -\frac{cos(\delta)\cdot cos(\alpha)+\frac{1}{tan(\theta^\prime)}\cdot sin(\delta)}{sin(\delta)\cdot cos(\alpha) -\frac{1}{tan(\theta^\prime)}\cdot cos(\delta)}\cdot \frac{1}{cos(\beta)}\)

右辺の分数の分子と分母とに\(tan(\theta^\prime)\)をかけ、式を整理すると、

\(tan(\xi^\prime) = \frac{sin(\delta) + tan(\theta^\prime)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta) – tan(\theta^\prime)\cdot sin(\delta)\cdot cos(\alpha) }\cdot \frac{1}{cos(\beta)}\)

を得ます。この式を見ると、正規型ユニバーサルジョイントを２つ組み合わせた場合の\(\theta\)と\(\xi\)との関係の式と同じであることがわかります。

この式の変形が意味する事は、簡易型ユニバーサルジョイントの解析に用いた基準点の取り方を工夫すれば、正規型ユニバーサルジョイントと同じ式が導出できた、ということです。簡易型ユニバーサルジョイントを２つ組み合わせたときの図に\(\theta^\prime\)と\(\xi^\prime\)とを加えたのが下図です。

これはどういうことかというと、簡易型ユニバーサルジョイントに、下図のようなピンに垂直な仮想的な補助ピンを加え、その先端を基準点の一つとすればよい、ということを言っています。

上図にて基準点示したのが下図となります。同一の垂直線上にある赤い点と青い点が簡易型ユニバーサルジョイントの解析をする際に用いた基準点に、仮想的な補助ピンの基準点を描き加えています。この仮想的な補助ピンの赤の基準点と青の基準点とを使って正規型のユニバーサルジョイントと同様の解析を進めることで、最終的には全く同じ結果が得られます。

ここまでの議論で、「簡易型ユニバーサルジョイントは、正規型ユニバーサルジョイントと等価である」ということがわかります。

簡易型ユニバーサルジョイントを2つ組み合わせた場合の解析を行います。正規型ユニバーサルジョイントを２つ組み合わせた図と同様のものを下記に示します。

前回の議論から、駆動面（赤の円）を移動する基準点の\(x\)軸に対する角度\(\theta\)と、伝達面（青の楕円）を移動する基準点の\(x\)軸に対する角度\(\varphi\)との間には次のような関係が成立します。

\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)

中継面（もう一つの青の楕円）を移動する基準点の\(x\)軸に対する角度\(\varphi^\prime\)と、最終伝達面（緑の円）を移動する基準点の\(x\)軸に対する角度を\(\xi\)とすると、\(\theta\)と\(\varphi\)との関係と同じ考え方で、

\(tan(\varphi^\prime) = tan(\xi)\cdot\frac{1}{cos(\beta)}\)

を得ることができます。

一点細かいことを補足しておくと、正規型ユニバーサルジョイントでは、動力を受ける側も伝える側も対称の関係にありましたので、\(\beta\)は、中継面（上の青い円）を基準とした角度としていましたが、簡易型ユニバーサルジョイントは対称ではありませんので、最終伝達面（上の緑の円）を基準とした角度としています。

さて、\(tan(\alpha+\beta)=\frac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)\cdot tan(\beta)}\)でしたので、

\(tan(\varphi^\prime) = tan(\varphi +\delta) = \frac{tan(\varphi)+tan(\delta)}{1-tan(\varphi)\cdot tan(\delta)}\)

となり、\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)を代入し、

\(tan(\varphi^\prime) = \frac{tan(\theta)\cdot\frac{1}{cos(\alpha)}+tan(\delta)}{1-tan(\theta)\cdot\frac{1}{cos(\alpha)}\cdot tan(\delta)}\)

分子と分母とに\(cos(\delta)\cdot cos(\alpha)\)をかけ、

\(tan(\varphi^\prime) = \frac{tan(\theta)\cdot cos(\delta) + sin(\delta)\cdot cos(\alpha)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\)

最終的に、

\(tan(\xi) = \frac{sin(\delta)\cdot cos(\alpha) + tan(\theta)\cdot cos(\delta)}{cos(\delta)\cdot cos(\alpha)-tan(\theta)\cdot sin(\delta)}\cdot cos(\beta)\)

を得ます。

正規型ユニバーサルジョイントの時と同様に、我々の興味のあるのは、\(\delta=0\)もしくは\(\delta=\frac{\pi}{2}\)の時です。

\(\delta=0\)の時は、下図のとおり、２つのピンが同位相となります。

この時、\(sin(\delta)=0\)、\(cos(\delta)=1\)ですので、

\(tan(\xi) = tan(\theta)\cdot \frac{cos(\beta)}{cos(\alpha)}\)

従って、\(|\alpha| = |\beta|\)であれば、\(\theta\)と\(\xi\)とは絶えず同じ角度であることがわかります。

\(\delta=\frac{\pi}{2}\)の時は、下図のとおり、２つのピンの位相が90°ずれます。

この時、\(sin(\delta)=1\)、\(cos(\delta)=0\)ですので、

\(tan(\xi) = -\frac{1}{tan(\theta)}\cdot cos (\alpha)\cdot cos(\beta)\)

\(= tan(\theta-\frac{\pi}{2})\cdot cos (\alpha)\cdot cos(\beta) \)

という関係を得ます。正規型ユニバーサルジョイントの場合と同様、\(\theta\)と\(\xi\)は、同じ角度ではないことがわかります。

これまで議論してきたユニバーサルジョイントとは異なり、模型では下図のように構成を簡素化したユニバーサルジョイントが使われることが多くあります。ここでは、これまで議論してきたものを正規型ユニバーサルジョイントと、簡素化したものを簡易型ユニバサールジョイントと呼ぶこととします。簡易型ユニバーサルジョイントについても、正規型ユニバーサルジョイントについて述べたことがそのまま成立するのか、見てみたいと思います。

以後の議論では、簡易型ユニバーサルジョイントの各部の名称を次のようにします。正式名称もしくはより一般的に使われる名称をご存じの方は、お知らせください。まず、下図の右側の動力源につなぐ、もしくは最終的に動力を伝達する部品で、上下2本伸びて円筒を切り欠いた部分を「爪」、そこに開いている長細い穴を「ガイド」、下図左側の部品でガイドにはまる部分を「ピン」、ピンに直交し動力を伝達する軸を「伝達軸」と呼ぶこととします。

簡易型ユニバーサルジョイントが回転する様子を下図に示します。ピンの中心は、青い線で示す平面上を移動します。ガイドの中心は、赤い線で示される平面上を移動します。実際には、ピンの位置がガイドに沿って移動する余地があるのではありますが、ここではピンの中心とガイドの中心とが交わる点は動かないという理想的な状態を仮定して議論を進めます。

上で述べたピンの中心とガイドの中心を立体的に見たのが次の図です。ピンと駆動軸の中心が交わるところを原点し、ガイドの中心位置の基準点（赤い点）が赤で示した水平面上の円形の軌道を移動するものとします。この時、赤い点を通る\(z\)軸方向の垂直な線と、ピンの中心軸とが交わった基準点（青い点）は、水平面に対して傾いた青で示した楕円形の軌道を移動します。なお、ガイドの中心位置の正確な位置については、下図では爪の内側の円筒面にあるものとして作図しましたが、赤の基準点と青の基準点とがz軸方向の垂直線上にある限り、爪の外側の円筒面でも、爪の厚みの中心でも構いません。

赤の点の座標を\((x,y,z)\)、青の点の座標を\((u,v,w)\)とします。原点\((0,0,0)\)と\((x,y,z)\)の距離を\(r\)としたときに、これらの2点を結ぶ直線が水平面上で\(x\)軸となす角度を\(\theta\)とします。また、原点\((0,0,0)\)と\((u,v,w)\)との距離を\(l\)とし、これらの2点を結ぶ直線が水平面に対して\(\alpha\)傾いた面で\(x\)軸となす角を\(\varphi\)とします。これを示したのが下図です。

この時、

\((x,y,z) = (r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

\((u,v,w) = (l\cdot cos(\varphi), l\cdot sin(\varphi)\cdot cos(\alpha), l\cdot sin(\varphi)\cdot sin(\alpha))\)

が成立します。

\((u,v,w)\)、\((x,y,z)\)は、垂直線上に位置しますので、\(u = x\)、\(v = y\)が成立します。したがって、

\(r\cdot cos(\theta) = l\cdot cos(\varphi)\)

\(r\cdot sin(\theta) =  l\cdot sin(\varphi)\cdot cos(\alpha))\)

という2つの式を得ることができます。下の式の左辺を上の式の左辺で、下の式の右辺を下の式の右辺で割ると、

\(\frac{r\cdot sin(\theta)}{r\cdot cos(\theta)} = \frac{l\cdot sin(\varphi)\cdot cos(\alpha)}{l\cdot cos(\varphi)}\)

となります。\(\frac{sin(\theta)}{cos(\theta)}=tan(\theta)\)でしたので、上記の式は

\(tan(\theta) = tan(\varphi)\cdot cos(\alpha)\)

と整理できます。従って、正規型ユニバーサルジョイントで得られた式に似た

\(tan(\varphi) = tan(\theta)\cdot\frac{1}{cos(\alpha)}\)

という関係を得ることができます。\(\varphi\)については、

\(\varphi = tan^{-1}(tan(\theta)\cdot\frac{1}{cos(\alpha)})\)

と計算することができます。

ここでの議論では必要ありませんでしたが、参考までに原点\((0,0,0)\)と\((u,v,w)\)との距離\(l\)を計算してみます。先ほどの2つの式について、左辺の二乗の和と、右辺の二乗の和は等しいので、

\(r^2\cdot sin^2(\theta) + r^2\cdot cos^2(\theta) = l^2\cdot cos^2(\varphi) + l^2\cdot sin^2(\varphi)\cdot cos^2(\alpha)\)

を得ます。\(sin^2(\theta)+cos^2(\theta)=1\)ですので、この式は

\(r^2=l^2(cos^2(\varphi)+sin^2(\varphi)\cdot cos^2(\alpha))\)

と変形できます。右辺の括弧の中は、

\(cos^2(\varphi) + sin^2(\varphi)\cdot cos^2(\alpha)\)

\(=cos^2(\varphi) + sin^2(\varphi)\cdot cos^2(\alpha) + sin^2(\varphi)\cdot sin^2(\alpha) – sin^2(\varphi)\cdot sin^2(\alpha)\)

\(=cos^2(\varphi) + sin^2(\varphi)\cdot (cos^2(\alpha) + sin^2(\alpha)) – sin^2(\varphi)\cdot sin^2(\alpha)\)

\(=cos^2(\varphi) + sin^2(\varphi) – sin^2(\varphi)\cdot sin^2(\alpha)\)

\(=1- sin^2(\varphi)\cdot sin^2(\alpha)\)

と整理することができます。

これをもとの式に代入し、

\(r^2=l^2(1-sin^2(\varphi)\cdot sin^2(\alpha))\)

を得、最終的に

\(l = \frac{r}{\sqrt{1- sin^2(\varphi)\cdot sin^2(\alpha)}}\)

\(= \frac{r}{\sqrt{1- sin^2( tan^{-1}(tan(\theta)\cdot\frac{1}{cos(\alpha)}))\cdot sin^2(\alpha)}}\)

を得ます。

 

 

 

大学の一般教養課程で、「図学」を学びました。3次元空間の物体の幾何学的な関係についての問題を2次元の紙の上に表現して解く、と言えばよいのでしょうか。白状すると、「とりあえず単位はもらいました」程度の成績だったのですが、その理由の一つは「解こうとしている問題の諸条件を的確に盛り込んだ図をフリーハンドで描く」ということが不得手である、ということだと思っています。

そういえば、フリーハンドで円を描くのが抜群に上手い物理の先生が高校にいました。数学とか物理とかが得意な人は、こういった図を的確に描く能力もあるのではないか、などということを思ったものでした。

そういう私にとって、CADツールは、図面を描く道具だけでなく、ウン十年前の鬱憤を晴らすというと大げさですが、図学的思考をする道具としても重宝しています。今回のユニバーサルジョイントの件も、頭を整理するのにずいぶんと役立ちました。

ということで、これまで式で表現してきたユニバーサルジョイントの基準点の関係を図で表現したものを載せておきます。dda40xさんの紹介されたT氏のようなエレガントな図にはできませんが、まぁ、こういう見方もある、程度で参考になれば幸いです。

下は、ジョイントを同位相にした場合の図です。①は駆動面を、②は伝達面を、③は中継面を、④は最終伝達面を、それぞれ正面から見た様子を示します。なお、駆動面と伝達面とがなす角度と、中継面と最終伝達面とがなす角度は（絶対値が）同じであるとします。

それぞれの位置でどのように見えるかを示したのが下の図です。

駆動面①の基準点は、半径\(r\)の赤い線上を移動し、\(\theta\) の角度にあるとします（赤い線）。また、伝達面②は、①の視点からは青い点線の楕円に見えます。この楕円の高さは、基準点の回転半径を\(r\)、駆動面に対する伝達面の傾きを\(\alpha\)としたとき、\(r\cdot cos(\alpha)\)となります。このとき、伝達面の基準点は青い点線の楕円を移動し、この楕円と\(\theta\)に直交した青い点線とが交わったところに位置します。

伝達面の視点で見たのが②です。①で見えた楕円の上の基準点は、この点から\(y\)軸方向に延ばした線と、青い実線の円と交差するところとなります。これが先に示した、

\(tan(\varphi) = tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\)

の式の意味するところです。実際にCADツールで作図して\(\varphi\)を計測してみると、上記の式で計算した値が得られます。

中継面の視点で見たのが③です。伝達面と中継面とは同位相ですから、中継面の基準点は、青い実線上ので\(\varphi\)の角度に位置します。中継面に直交する最終伝達面の基準点は\(\varphi\)に直交した角度で、緑の点線の楕円の上を動きます。

最終伝達面の視点で見たのが④です。これは①と②との関係と同じで作図すればよく、緑の点線の楕円上の点から\(y\)軸方向に延ばした線と緑の実線の円と交差する点に基準点が位置します。図から赤い実線と緑の実践とが平行であることがわかると思いますが、実際にCADツールで計測しても\(\xi=\theta\)であることがわかります。

次は、伝達面②と中継面③との基準点を９０度(\(\frac{\pi}{2}\))ずらした場合を考えます。

この場合、駆動面①、伝達面②、中継面③、最終伝達面④を正面から見るとどうなるか、というのが下の図です。今回も、駆動面と伝達面とがなす角度と、中継面と最終伝達面とがなす角度は（絶対値が）同じであるとします。

まず、①、②の図は前回と全く同じとなります。③の中継面の基準点は②の伝達面の基準点に直交しますのでその角度は異なりますが、③、④で作図する方法は前回と同じ考え方です。

もともとの期待は、最終伝達面④の基準点の角度\(\xi\)が、伝達面①の基準点の角度\(\theta\)に対して９０度異なる角度にあるということですが、この図は、そうはならない、ということを示しています。

②と④とを見ていただければわかりますが、②で\(\theta-\frac{\pi}{2}\)に対して\(\varphi\)は角度が進み、④でさらに\(\xi\)で角度が進む、ということがわかります。これが、前回導出した

\(tan(\xi) = tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

の式の意味するところです。

次に、２つのユニバーサルジョイントを組み合わせる事を考えます。

まず、前回の議論で、駆動面に対し伝達面が\(\alpha\)だけ傾いている場合、駆動面を回転する基準点の\(x\)軸に対する角度\({\theta}\)と、伝達面を回転する基準点の\(x\)軸に対する角度\({\varphi}\)とには、次の関係が成立することを示しました。

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot\frac{1}{cos(\alpha)}\)

この伝達面の先に、もう一つのジョイントをつなげることを考えます。下図にこの様子を示します。

図の下にある赤の円が駆動面で、青の円が伝達面を示します。それぞれの基準点の角度が\(\theta\)、\(\varphi\)となります。

もう一つのジョイントの十字型部品の基準点の移動する円を２つ、図の上の方に青の円と緑の円とで示します。ここでは、青の円を中継面、緑の円を最終伝達面、と呼ぶこととします。なお、議論を簡単にするために、ここでは駆動面につながっている軸、伝達面と中継面をつなぐ軸、最終伝達面につながっている軸、の３つは、同一平面上にあるものとします。

中継面は伝達面と平行であり、その中継面上を移動する基準点の角度を\(\varphi\prime\)とし、伝達面の基準点の角度\(\varphi\)に対して、\(\varphi\prime=\varphi+\delta\)という関係が成り立つものとします。つまり\(\delta=0\)であれば、ジョイントは同位相で、\(\delta=\frac{\pi}{2}\)であれば、ジョイントは90度ひねられて取り付けられていることとなります。

また、最終伝達面は、中継面に対して\(\beta\)傾いているものとし、最終伝達面の基準点の角度を\(\xi\)とします。

さて、中継面の基準点の角度\(\varphi\prime\)と最終伝達面の基準点の角\(\xi\)との関係は、\(\theta\)と\(\varphi\)との関係と同じで、次の式が成り立ちます。

\(tan(\xi)=-\frac{1}{tan(\varphi^\prime)}\cdot\frac{1}{cos(\beta)}\)

\(\varphi^\prime=\varphi+\delta\)でしたので、上記の式は、

\(tan(\xi)=-\frac{1}{tan(\varphi+\delta)}\cdot\frac{1}{cos(\beta)}\)

となります。

上記の式の中の\(tan(\varphi+\delta)\)に注目します。2つの角度の和のタンジェントは次のように書き変えることができます。

\(tan(\varphi+\delta)=\frac{tan(\varphi)+tan(\delta)}{1-tan(\varphi)\cdot tan(\delta)}\)

\(tan(\varphi)=-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\)を代入すると、

\(tan(\varphi+\delta)\) = \(\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+tan(\delta)}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot tan(\delta)}\)

となり、\(tan(\delta)=\frac{sin(\delta)}{cos(\delta)}\)であったことを思い出し、分子と分母とに\(tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)\)をかけると、

\(tan(\varphi+\delta)=\frac{-\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}+\frac{sin(\delta)}{cos(\delta)}}{1+\frac{1}{tan(\theta)}\cdot \frac{1}{cos(\alpha)}\cdot \frac{sin(\delta)}{cos(\delta)}}=\frac{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}\)

これを、最初の式に代入すると

\(tan(\xi)=-\frac{1}{tan(\theta+\delta)}\cdot \frac{1}{cos(\beta)}=-\frac{tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)+ sin(\delta)}{-cos(\delta)+tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

となり、少し見やすく整理すると、

\(tan(\xi)=\frac{sin(\delta)+tan(\theta)\cdot cos(\delta)\cdot cos(\alpha)}{cos(\delta)-tan(\theta)\cdot sin(\delta)\cdot cos(\alpha)}\cdot \frac{1}{cos(\beta)}\)

という式が得られます。

さて、いつも議論となるのは、ジョイントが同位相か、\(\frac{\pi}{2}\)（90度）ひれらているかです。

上の図のように、ジョイントを同位相とするということは、\(\delta=0\)とするということですので、\(sin(0)=0\)、\(cos(0)=1\)となります。これを代入すると

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}\)

となります。従って、\(\alpha=\beta\)であれば、

\(tan(\xi)=tan(\theta)\)

となります。

この式は、ジョイントを同位相にし、2つのジョイントの傾きを同じにしておけば、一方のジョイントの不等速性は、もう一方のジョイントで打ち消され、駆動面と、最終伝達面との位相とは、同じであり、等速性が保証される、ということとなります。

また、\(cos(\theta)=cos(-\theta)\)であったことを思い出すと、上記の式は、

\(tan(\xi)=tan(\theta)\cdot \frac{cos(\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(\beta)}=tan(\theta)\cdot \frac{cos(\alpha)}{cos(-\beta)}=tan(\theta)\cdot \frac{cos(-\alpha)}{cos(-\beta)}\)

のいずれでも成立することがわかります。つまり、上で述べたジョイントの2つの傾きが同じ、というのは、傾きの絶対値が同じと言い換えてよいことがわかります。

上の図のように、ジョイントを90度回転させると、\(\delta=\frac{\pi}{2}\)となりますので、\(sin(\frac{\pi}{2})=1\)、\(cos(\frac{\pi}{2})=0\)を先ほどの式に代入すると、

\(tan(\xi)=-\frac{1}{tan(\theta)\cdot cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、少し変形すると、

\(tan(\xi)=tan(\theta-\frac{\pi}{2})\cdot\frac{1}{cos(\alpha)}\cdot\frac{1}{cos(\beta)}\)

となり、ユニバーサルジョイント1個の時によく似た形の式となります。異なるのは、\(\frac{1}{cos(\beta)}\)が付け加わっていることです。

ユニバーサルジョイント1個の時は、駆動面の基準点の角度に比して、伝達面面の基準点の角度が進む、ということでしたが、ユニバーサルジョイント2個の際は、さらにもう一回角度が進むこととなり、つまりは、不等速性を増大させる、ということがわかります。

（この項続く）

 

数学でベクトルという概念があり、その基本的な性質の一つが、「直交する2つのベクトルの内積は0になる」というものです。わかりやすく言うと、原点\((0,0)\)から、座標\((x,y)\)を結んだ線と、原点\((0,0)\)から、座標\((u,v)\)を結んだ線とが直交する、つまり90度で交わる場合、\(x \cdot u + y \cdot v\)は必ずゼロになるということです。

直交するベクトルの内積が0になるというのは、3次元空間でも成り立ち、３次元の座標\((x,y,z)\)と\((u,v,w)\)とがあったときに、原点\((0,0,0)\)とこれらを結ぶ２つの線が直交する場合は、\( x \cdot u + y \cdot v + z \cdot w =0\)が成立します。

ユニバーサルジョイントの十字型の部品の２つの軸は直交していますので、２つの基準点の座標についても、上記の性質が成り立ちます。

\((x,y,z)=(r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

\((u,v,w) = (r\cdot cos(\varphi), r\cdot sin(\varphi)\cdot cos(\alpha), r\cdot sin(\varphi)\cdot  sin(\alpha))\)

でしたので、

\(r \cdot cos(\theta) \cdot r \cdot cos(\varphi) + r \cdot sin(\theta) \cdot r \cdot sin(\varphi) \cdot cos(\alpha) + 0\cdot r \cdot sin(\varphi)\cdot sin(\alpha) = 0\)

となります。式を整理すると、

\(r ^2 \cdot sin(\theta) \cdot sin(\varphi) \cdot cos(\alpha) = – r ^2 \cdot cos(\theta) \cdot cos(\varphi)\)

となり、両辺を\(r^2 \cdot cos(\varphi) \cdot sin(\theta)\cdot cos(\alpha) \)で割ると、

\(\frac{sin(\varphi)}{cos(\varphi)} = – \frac{cos(\theta)}{sin(\theta) \cdot cos(\alpha)}=-\frac{1}{\frac{sin(\theta)}{cos(\theta)}}\cdot\frac{1}{cos(\alpha)}\)

\( \frac{sin(\theta)}{cos(\theta)}=tan(\theta) \) でしたから、この式は

\(tan(\varphi) = – \frac{1}{tan(\theta)} \cdot \frac{1}{cos(\alpha)}\)

となります。\(tan\)の周期性の性質を利用してもう少し変形すると、

\(tan(\varphi) = tan(\theta-\frac{\pi}{2})\cdot \frac{1}{cos(\alpha)}\)

という式が得られます。\(\theta =\frac{\pi}{2}\)の時、\(\varphi=0\)となるのでした。従って、この式が基準点の位置関係を的確に表現しています。

説明がこなれていないですが、この式からわかることを書いてみたいと思います。

\(\alpha > 0 \)を想定していますので、\(cos(\alpha) < 1\)となります。従って、\(tan(\varphi)\)は、\(tan(\theta-\frac{\pi}{2})\)より大きな値になります。このことは、\(\varphi\)は、\(\theta-\frac{\pi}{2}\)よりも角度が大きい、つまり、伝達面の基準点の回転角は、駆動面の基準点の基準点の回転角よりも進んでいる、ということを示しています。

\(\frac{1}{cos(\alpha)}\)の影響を受けない場合があり、それは両辺の\(tan\)が\(0\)か\(\infty\)となる場合で、その組み合わせは

\(\theta=\frac{\pi}{2}, \varphi=0\)

\(\theta=\pi, \varphi=\frac{\pi}{2}\)

\(\theta=-\frac{\pi}{2}, \varphi=\pi\)

\(\theta=0, \varphi=-\frac{\pi}{2}\)

の４つです。これらが成立するのは、基準点のいずれかが、\(x\)軸上にあるときで、\(\frac{\pi}{2}\)つまり、90度ごとに駆動面と伝達面との基準点の回転角が一致するものの、それ以外は、伝達面の基準点の回転角の方が大きくなるということで、このために不等速性が発生するということが言えると思います。

さて、上記の式を\(\varphi\)について解くと、

\(\varphi = tan^{-1}(\frac{tan(\theta-\frac{\pi}{2})}{cos(\alpha)})\)

となります。この計算式を使えば、駆動面の基準点の角度が与えられたときに、伝達面の基準点の角度を計算することができます。

 

ユニバーサルジョイントを構成する十字型の部品の2つの軸の先端がどこを動くか、を示したのが次の図となります。ここで、十字型の部品の中心、つまり、２つの軸が交差する点を原点\((0,0,0)\)とします。また、水平面上（赤い円）を移動する軸に取り付けられたフォーク状の部品に動力が供給され、それが傾いた面上（青い円）を移動する軸に伝達されるとします。ここでは仮に、水平な面を「駆動面」と、傾いた面を「伝達面」と呼ぶこととします。

原点と十字の二軸のそれぞれの一方の先端だけに注目したのが、次図です。以下、この注目した軸の先端を「基準点」と呼ぶこととします。基準点の選び方によって、多少式が変わってきますが、最終的には同等の結果が得られます。

駆動面を動く基準点は、原点\((0,0,0)\)を中心に、水平面上の半径\(r\)の円を回転し（上図の赤い円）、伝達面を動く基準点は、原点を中心に、駆動面に対して角度\(\alpha\)傾いた面の上の半径\(r\)の円を回転します（同じく青い円）。

このとき、駆動面の基準点の座標を\((x,y,z)\)、伝達面の基準点の座標を\((u,v,w)\)であるとします。更に、\((x,y,z)\)の駆動面における\(x\)軸に対する角度を\(\theta\)とし、\((u,v,w)\)の伝達面における\(x\)軸に対する角度を\(\varphi\)とします。

駆動面の基準点の座標は、三角関数の定義から、

\((x,y,z)=(r\cdot cos(\theta), r\cdot sin(\theta), 0)\)

となります。

伝達面の基準点の座標を求めると、まず\(x\)座標の値\(u\)は、被駆動面の傾きによらず、

\(u = r\cdot cos(\varphi)\)

となります。

座標\((u,v,w)\)と座標\((u,0,0)\)の距離は、\(r\cdot sin(\varphi)\)となります。座標\((u,0,0)\)、\((u,v,0)\)、\((u,v,w)\)からなる直角三角形を考えると、この底辺の長さ、高さがそれぞれ\(u\)、\(v\)となり、伝達面の傾きが\(\alpha\)なので、

\(v = r\cdot sin(\varphi)\cdot cos(\alpha)\)

\(w = r\cdot sin(\varphi)\cdot sin(\alpha)\)

となります。まとめると、

\((u,v,w) = (r\cdot cos(\varphi), r\cdot sin(\varphi)\cdot cos(\alpha), r\cdot sin(\varphi)\cdot  sin(\alpha))\)

となります。

 

念のため、今回の議論に必要となる最低限の三角関数の復習をしておきます。

原点\((0,0)\)から長さ\(r\)の線分が傾き\(\theta\)でひかれているとします。

このとき、線分の先端の座標は\((r\cdot sin(\theta),r\cdot cos(\theta))\)となります。

また、\(sin(\theta)\)を\(cos(\theta)\)で割った値を\(tan(\theta)\)と呼びます。つまり、

\(tan(\theta)=\frac{sin(\theta)}{cos(\theta)}\)

です。

角度の表現は、一般に使われる度ではなく、ラジアン表現を使います。ここでは、\(\pi=180^{\circ}\)、\(\frac{\pi}{2}=90^{\circ}\)ということだけ思い出していただければ結構です。

いくつか代表的な値をあげておくと、

\(sin(0)=0\)

\(cos(0)=1\)

\(sin(\frac{\pi}{2})=1\)

\(cos(\frac{\pi}{2})=0\)

となります。

このほか、以下の式が成立します。

\(tan(\theta-\frac{\pi}{2})=tan(\theta+\frac{\pi}{2})=-\frac{1}{tan(\theta)}\)

\(cos(\theta)=cos(-\theta)\)

また、2つの角度の和のタンジェントはそれぞれの角度のタンジェントを用いて、次のように表現できます。

\(tan(\alpha+\beta)=\frac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)\cdot tan(\beta)}\)

今回の議論で必要な三角関数に関する知識は、以上です。

本格的に三角関数を復習されたい方は、以下のビデオがわかりやすいかと思います。

２つの軸が斜めに接続されて回転するということは、そもそもどういうことかということを考えてみたのが下の図です。

２つの軸は緑色の斜めの線で示した面で接します。2つの赤い矢印の位置を絶えず一致するようにすれば、2つの軸は同じ速度で回転することになります。この図の通りの機構を実現しようとすると、折れ曲がっている軸の内側に注目している位置が来たときは軸が縮み、（上図の水平軸の\(l_2\))、軸の外側に来たときは軸が伸びる（上図の水平軸の\(l_1\))ような機構をつくらなければなりません。このような「回転に応じて伸び縮みする」ような機構をリーズナブルなコストで作るのはきわめて大変なこととなります。

ユニバーサルジョイントは、下図のように、２つの軸が90度で交差する十字型の部品１つと、2つのフォーク型の部品とを組み合わせて、折れ曲がって回転することができる軸を簡単に実現することができます。

実際の回転する様子を示す動画がWikipediaに記載されています。

ユニバーサルジョイントをつなげて一方の軸を傾けた状態を真横から見たのが下の図です。十字型の部品の軸の一方の先端は、赤で示した水平面上の線の上を移動します。他方の軸のの先端は、青で示した、水平面に対して傾いた面の上を移動します。

この中には、最初の図に示した、2つの軸が接合する緑の面に相当するものは存在しません。2つの軸の十字の先端が、どのような座標位置となるか、今回の興味の対象となります。

余談となりますが、等速ジョイントとしてWikipediaに紹介されているZeppa Jointは、２つの軸の交差する位置に、黄色な小さなボールを入れており、これらのボール群がなす軌跡が、最初の図の緑の線で示した接合面を実現していると考えることができます。