前回までに説明した方針にて、次のような図面を作成しました。まずは4線用のもの。
こちらは２線用のもの。基本寸法は4線用のものと同じで、橋梁部分を間引いたものとなります。
これらの図面をもとに、部品の図面を作成作成します。実物では、左右の橋脚部分と橋梁部分とをガセットで繋げる構造になっていると理解していますが、そのあたりは組み立てやすさ、強度を優先した簡易的な構造としました。もちろん、見た目にも違和感のないように配慮しています。
以下が4線用のSignal Bridgeの部品の図面となります。
そしてこちらが2線用のSignal Bridgeの部品図面です。
これらの図面からdxf形式に落としたものを業者に渡すと、レーザカットしたステンレスの部品が出来上がりますので、あとは組み立てるのみです。
これらのSignal Bridge用のガセット・プレートを打ち出すための図も以下の通りに用意しました。上半分が4線用のもの、下半分が２線用のものとなります。
次回は、これらを実際にどう組み立て行くかをイラストにて紹介いたします。
Signal Bridgeのプロタイプは決まりましたので、あとはその図面を元に粛々と設計するのみです。本物の寸法を参考にしつつ、レイアウトの建築限界や線路配置をもとに、妥当な寸法を決めてゆきました。
悩んだのが、ガセットの構造の表現です。実物では次のように、ガセットの両面に、L字鋼を互い違いにしてリベットで固定しているのが一般的と思われます。
街の中を見回してみると、送電線の鉄塔とか、携帯電話の基地局とか、いたるところにこの構造を見つけることができます。そして、この立体感はそれなりに目立つので、これを表現できないかと考えました。
しかしながら、レーザーカットでできるのは、板を寸法通りに切断することで、深さ方向の加工はできません。となると、このL字鋼の構造を表現するには、別に部品を切り出して、取り付ける必要があります。そこまですると、ガセットの表のL字鋼、ガセット、ガセット裏のL字鋼、という、立体的な構造を表現する必要があり、部品点数も増え、組み立ても面倒となります。
これは、もともとの方針の一つであった、「レーザーカットを使って簡単に作る」、ということに反します。L字鋼の表現はあきらめ、レーザーカットした板に、リベットを打ち出した板を貼り付ける、という簡略化した設計にする、という結論としました。
dda40xさんのレイアウトは、高効率の駆動システム、低抵抗車輪を中心とした、「走り」に関する様々な技法を総合的に統合したものを見せる、という点に一番の主眼が置かれていると思っています。そこで一番の主役となるのは、それらの技法を取り込んだ車輛群であり、今回作成するSignal Bridgeは、基本的には脇役だと考えます。その脇役に過度の労力をかけるのは得策ではないと考えます。
もちろん脇役だから手を抜いてよいということではなく、１）実物の構造や寸法に則った設計となっていること、２）簡単に作ることができ、頑丈であること、３）仕上がりがすっきりしており、レイアウトに置いたときにさりげない存在感を示すこと、が重要と考え、設計を進めました。
ずいぶん時間が経ってしまいましたが、dda40xさんのレイアウトのSignal Bridgeを設計した話を書いておきます。
こちらが当初レイアウトに置いてあったプラスチック製の信号橋です（写真はdda40xさんのblogから拝借しました）。
2つのプラスチック製の信号機を組み合わせたものなので、接合部が弱く信頼性がないということに加え、下の赤い矢印のところがトラス構造となっていないのがおかしいというのがdda40xさんのご指摘で、ステンレスのレーザカットを使って、頑丈で、構造上正しいものを作ろう、ということで設計を始めました。
早速、参考になる資料を探そうと、Pennsylvania鉄道の図面を検索してみると、次のような図面が出てきます(http://www.trainweb.org/s-trains/photos/projects/signal_b.gifより借用）。
上記のSignal Bridgeの模型は明らかにこの図面をもとに作ったものと思われます。そして、Pennsylvania Railroadの正式な図面のように見えます。Standard Railroad of the worldを標榜したPennsylvania Railroadが基本的な構造上の間違いをするとも思えず、釈然としなかったので、実際はどうだったのだろうということをまず確認することとしました。実物の画像がないかとGoogle検索してみると、このBlogのPRR Main Line Survey 2009というシリーズに、旧PRRのMainlineのSignal Bridgeを記録した12回のシリーズを見つけました。ただ、このシリーズの画像は、ほぼ真正面から撮影したものなので、それはそれで貴重な情報ではあるのですが、実際にSignal Bridgeがどういう構造になっているのか、よくわかりません。
これを手掛かりに、いくつかの場所に目星をつけ、ストリートビューでようやく見つけたのがこれです。
これを見ると、実物のSignal bridgeの左右の支柱の構造は、プラ製のものとは全く異なることがわかります。プラ製の製品ものはL字型の材料を組み合わせた構造になっていますが、実物は、H型の構造を作っています。
これを理解して先ほどの図面をよく見ると、確かになるほど、と納得できるところがあります。要はこのプラ製品はリサーチ不足だったということなのでしょうね。
さて、先ほどのストリートビューを見ればわかる通り、後ろに新しいSignal Bridgeが控えています。これは2019年7月の撮影のものですが、古いものはほどなく撤去されたようで、最新のストリートビューを見ると、新しいものしか残っていません。Pennsylvania Railroad時代からつい数年前まで使われていたということですから、長寿だったということが言えると思います。
さて、先ほどの図面を探している最中に、別の図面を見つけました(http://prr.railfan.net/standards/standards.cgi?plan=61940–より借用)。
この構造のSignal Bridgeがないかと、ストリートビューで探したのが次のものです。
こちらはPSCが製品化したものもあり、最初に見つけたSignal Bridgeに比べて、L字型の鋼材を組み合わせた、作りやすい構造になっていると思われましたので、こちらをベースに設計することとしました。
長々と続けてきた、ユニバーサルジョイントの正しい使い方のシリーズの目次をこちらに用意しておきます。今読み返すと書き足りないと思うこともありますが、追々直してゆきたいと思っています。またグラフの表示のプラグインの改訂により、当初の表示が乱れているところもありますが、こちらも直してゆきます。
また、同じ内容を固定ページにも用意しておきます。
（１０） – 簡易型ユニバーサルジョイントを正規型ユニバーサルジョイントと比較する
（１２） – ユニバーサルジョイントを2つ組み合わせた際の角速度を計算する
（１６） – MPギアを例に |α|≠|β|の場合の具体的な数値を当てはめる
（１９） – 阿里山のShayのαとβとの具体的な数値をあてはめる
（２２） – ２つのベクトルのなす角と外積とを使って解析に必要な角度を求める
（２３） – 3つの軸が同一平面に存在しない場合の角速度の変動（MPギアの場合）
（２４） – 3つの軸が同一平面に存在しない場合の角速度の変動（MPギアの場合-モーターの左右のジョイントの角速度の変動の解析）
4回前の記事でまとめをしてこのシリーズは完結するはずでしたが、考慮すべき事ができ、3回ほど記事を続けました。今回がたぶん本当のまとめになると思います。前回のまとめと重複する部分がほとんどですが、このシリーズで考察してきた事を、改めて以下にまとめます。
（１）まずはユニバーサルジョイントの使い方一般について。
（２）模型では、簡易型のユニバーサルジョイントがよく使われます。こちらについても解析を行い、次の結果を得ました。
（３）日本型の電車を中心に、MPギア（もしくはそれに類似する形態の駆動系、以下MPギアで代表）がよく用いられています。こちらの考察を進め、次のような結論や仮説を得ました。
（４）ユニバーサルジョイントを構成する3つの軸が同一平面にない場合の解析も行いました。その結果次の結論を得ました。
最初に述べた、ピンの向きを揃える、を念のため下に図示します。
下は誤った使い方の図です。
ユニバーサルジョイントのモータへの正しい取り付け方も図示します。
誤った取り付け方を下に示します。
それでは、長々と続いてきたシリーズを終わりにしたいと思います。
このシリーズを続けるに当たって、示唆をいただいた方、貴重な情報をいただいた方に改めて御礼申し上げます。ありがとうございました。
前回、前々回と、MPギアのような駆動系でモーターの左右にユニバーサルジョイントで動力を伝道する場合に、モーターに取り付けるユニバーサルジョイントの位相が揃っていないと(\(\Delta\neq 0\))、左右のユニバーサルジョイントの最終伝達面の角速度が異なる、というを明らかにし、\(\Delta=\frac{\pi}{2}\)の場合を計算するとその左右の角速度比の変動が最大になり、かつかなり大きな値になるということを示しました。
これを踏まえてこれまでの議論を整理すると、MPギアを使った車両がカーブを走行する際には、２つの角速度の変動が車両の挙動に影響を与えることが考えられます。
１つめは、ユニバーサルジョイント単体で発生する角速度の変動です。カーブでは、ユニバーサルジョイントの折れ曲がり方が同じではない(\(\alpha\ne\beta\))ので、この変動は避けられません。しかしながら、ユニバーサルジョイントの位相をそろえる(\(\delta=0\)とする)ことで、この変動を最低限にすることができます。
そして、２つめは、今回議論したように、モーターに取り付ける2つのユニバーサルジョイントの位相が揃っていないことによって発生する、左右のユニバーサルジョイントの最終伝達面の角速度の差です。つまり、最終的な車輪の回転速度が左右の台車で異なる、ということです。これは\(\Delta=0\)とすることで防げますので必ず守るべきであると言えます。念のため、前々回掲載した図で言えば、左のような取り付け方法をとらなければならない、ということです。
定性的には、前者は車両の速度が一定しない（脈動する）ことに、後者は前後の台車の速度が異なる事による効率の低下やスムーズではない挙動に、つながると考えます。
以前MPギアの解析を行ったときにたてた、「角速度の変動率が5%に近づくあたりから、スムーズな走行に影響を与える」という仮説は\(\Delta=0\)であった場合にのみ成り立つものです。仮に\(\Delta=\frac{\pi}{2}\)であったとすると、角速度の変動率が8%を超えるあたりから、ということが言えるかと思いますが、2つの角速度の変動のうちどちらが支配的な影響を与えるか、については実験を行わないとわからないと思います。
いずれにしても、上記の仮説は一旦取り下げることといたします。
前回の記事で、モーターの左右に取り付けるユニバーサルジョイントに関し、その取り付け部分の位相\(\Delta\)を揃えておかないと、左右のユニバーサルジョイントの最終的な角速度に差が出ることを示しました。
実際にどれくらいの差が出るかを、以前解析に用いたモハ185を題材として計算してみます。まず、前回の計算結果のグラフを再掲します。半径600mmと500mmとで、ユニバーサルジョイントの位相が正しい(\(\delta=0\))場合と、間違っている(\(\delta=\frac{\pi}{2}\))場合の角速度の変動を示したものです。
\(\Delta=0\)の場合は、\(\delta=0\)、\(\delta=\frac{\pi}{2}\)にかかわらず、左右の角速度は同じという結論を前回の議論で得ましたので、以下では\(\Delta=\frac{\pi}{2}\)、つまりモーターに取り付けられたユニバーサルジョイントの位相が90度ずれている場合を考えます。
まず、R600で\(\delta=0\)の場合、左右の角速度の比がどうなるかを示したのが下図です。左側のユニバーサルジョイントの角速度比、右側のユニバーサルジョイントの角速度比も併せて示します。
このグラフを見てわかることは、左側のユニバーサルジョイントの角速度の変動、右側のユニバサールジョイントの角速度の変動は以前求めたものと全く同じもので、ユニバーサルジョイントに取り付ける側のジョイントの位相が\(\frac{\pi}{2}\)(90度)ずれていることで、グラフも\(\frac{\pi}{2}\)ずれています。その結果、左側の角速度比が最大（最小）になる時に、右側の角速度比が最小（最大）になります。ユニバーサルジョイント単体の角速度の変動は±3%弱に抑えられていますが、左右の角速度比は±6%程度になることがわかります。
次にR500で\(\delta=0\)の場合のグラフを示します。
カーブが急になったことで、ユニバーサルジョイント単体の角速度の変動は±4%程度になり、左右の角速度の比は±8%程度となっています。
\(\delta=\frac{\pi}{2}\)の時、ユニバーサルジョイント単体の位相が90度ずれている場合、ユニバーサルジョイント単体の角速度の変動が大きくなりますので、更に条件が悪くなることが考えられます。R600の場合、R500の場合のグラフを続けて示します。
R600の場合にユニバーサルジョイント単体の角速度比の変動が±4%程度のものが左右比で±9%程度までに拡大すること、R500の場合はユニバーサルジョイント単体の角速度比の変動が±6%程度のものが左右比で±13%程度までに拡大すること、がわかります。
ここまで、\(\Delta=\frac{\pi}{2}\)の場合を考えましたが、先ほど議論した通り\(\Delta\ne 0\)の時は、左右の角速度の変動が\(\Delta\)分ずれるので、左右のユニバーサルジョイントの角速度比の変動が必ず発生します。
わざわざ示すまでもないかもしれませんが、\(\Delta=\frac{\pi}{6}\)(30°)、\(\Delta=\frac{\pi}{3}\)(60°)、\(\Delta=\frac{\pi}{2}\)(90°)、のそれぞれの場合に、左右のユニバーサルジョイントの角速度比がどう変わるかを、R600の場合とR500の場合とについて示します。
長くなったので、今回の結論は次回にまとめます。
前回のまとめの投稿で、本質的に書くべきことはすべて網羅したと大見えを切りましたが、マーフィーの法則よろしく、一つ重要なことを見落としていたことに気づきました。
MPギアの解析の際に、「左右対称なので、同じ条件で解析できる」ということを述べました。確かに、左右のそれぞれのユニバーサルジョイント単体の挙動は同じ条件で解析できるのですが、そもそもモーターの左右のユニバーサルジョイントのモーター側の基準点の位相が揃っているか、を考慮しなければなりませんでした。
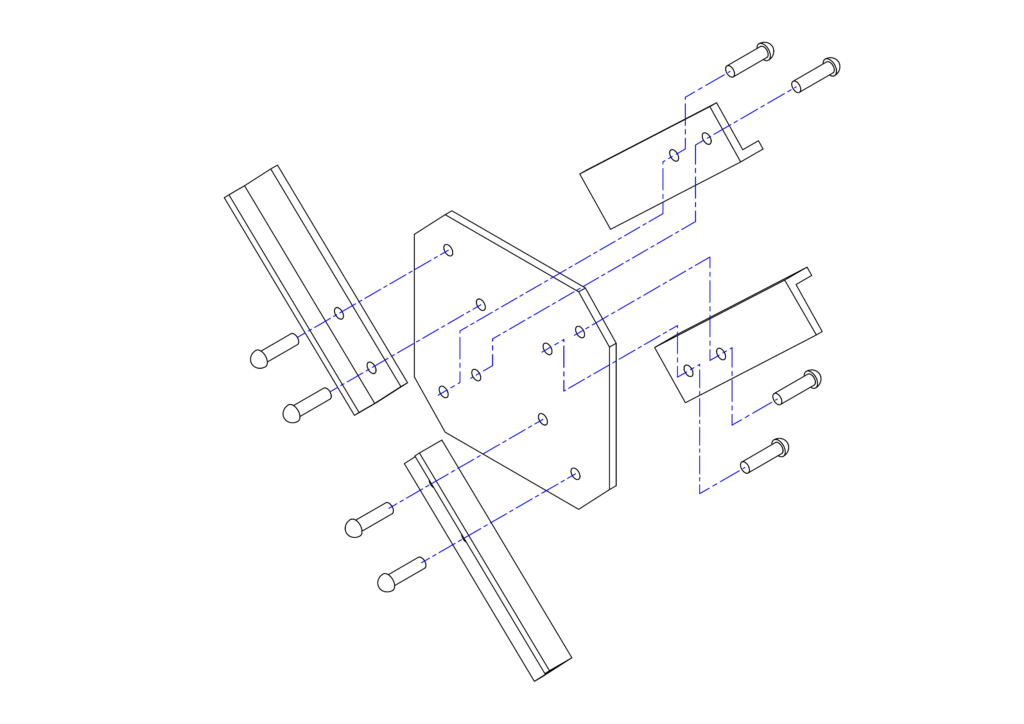
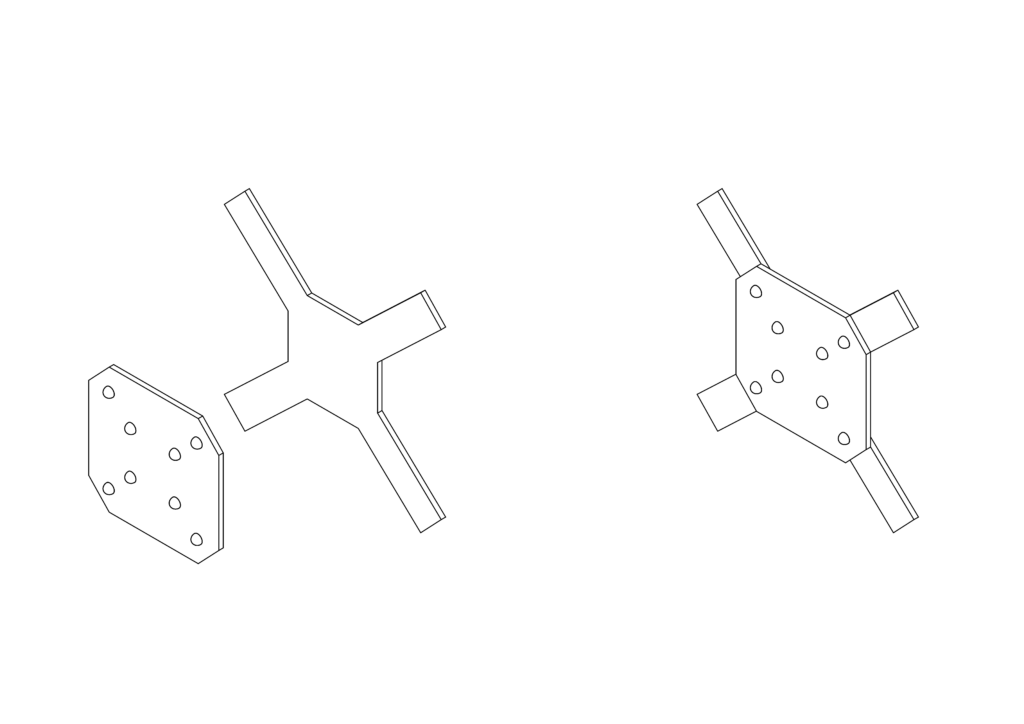
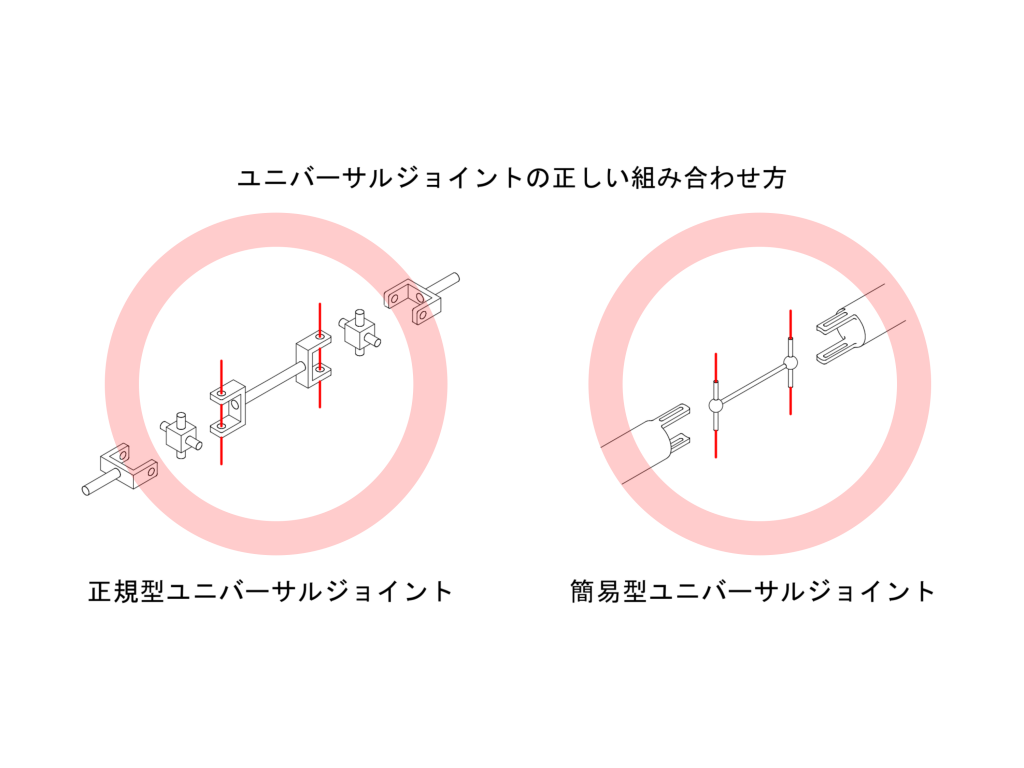
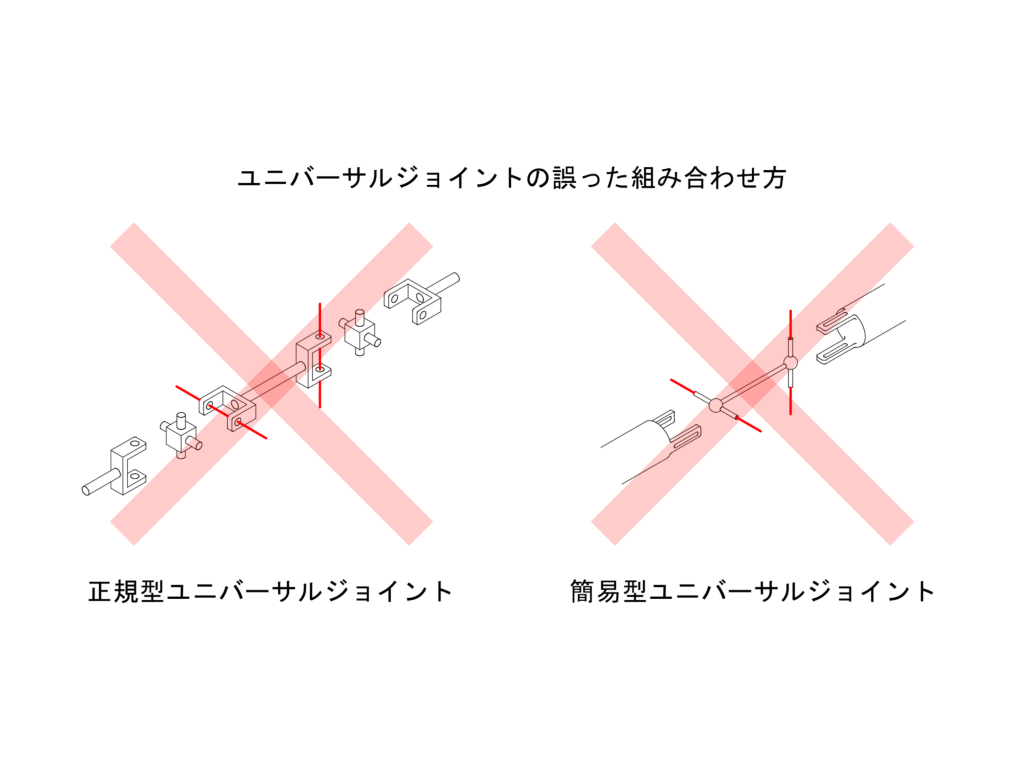
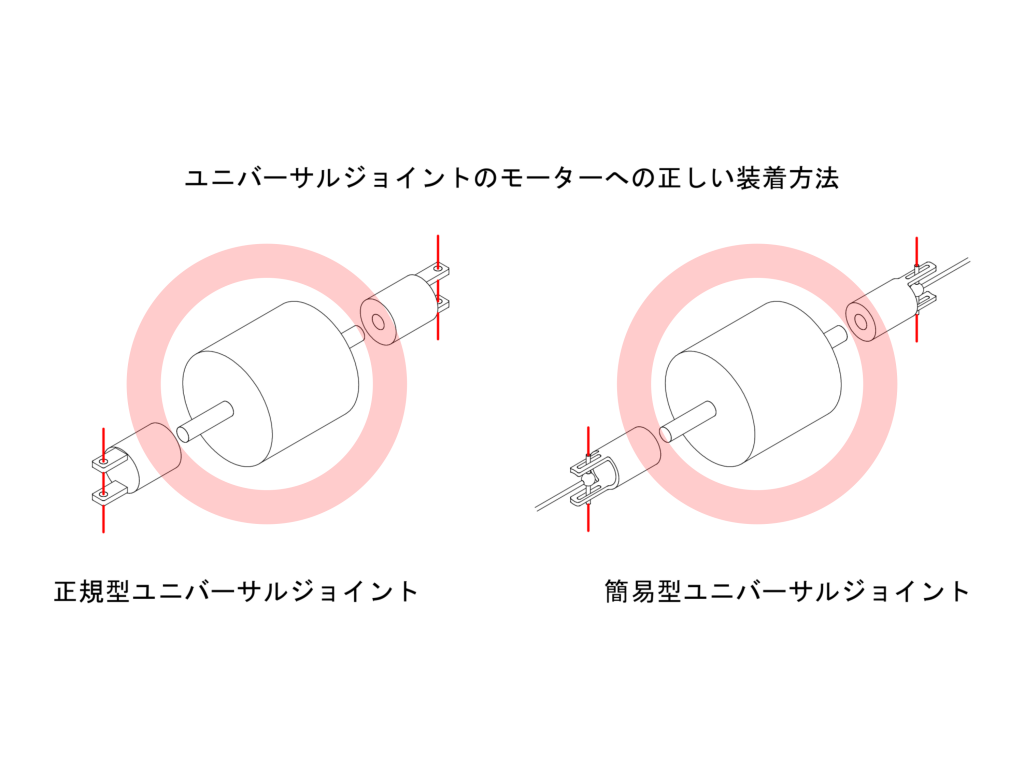
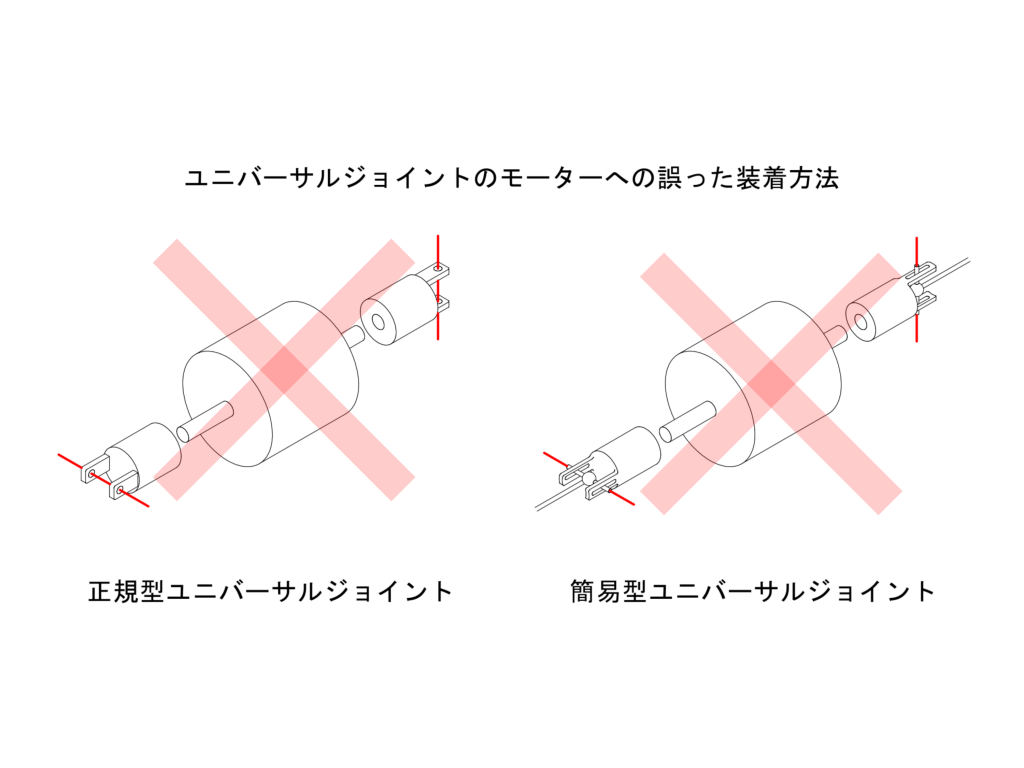
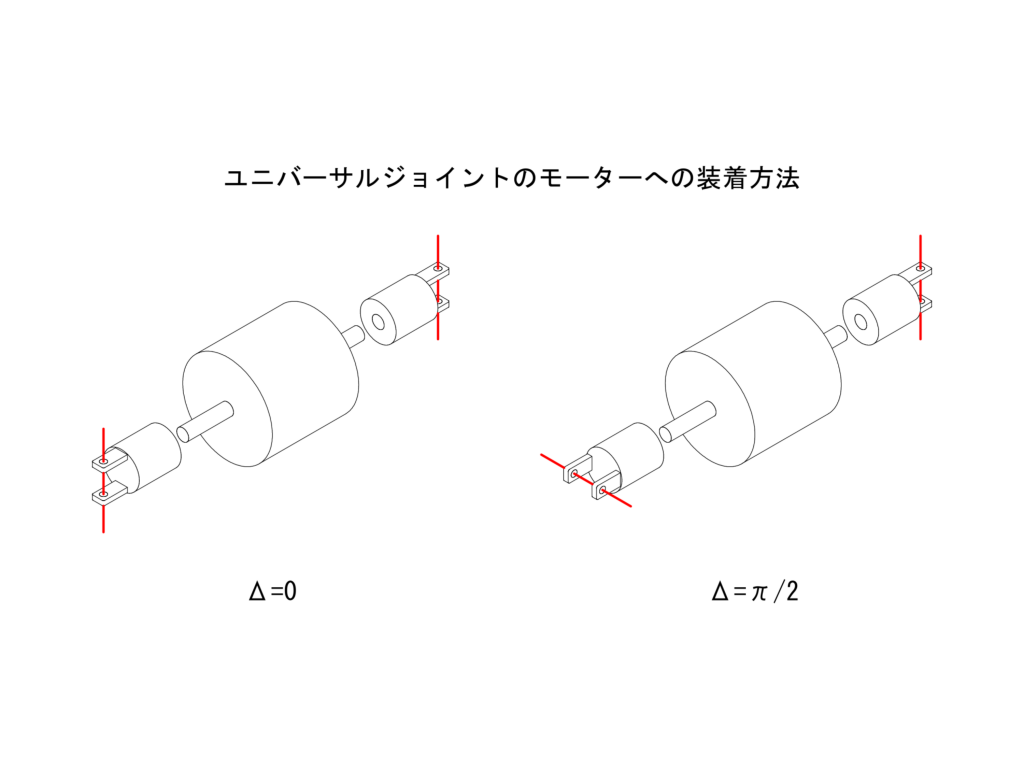
ここまでの議論は、下図左側に示したように、モーター側のジョイントの位相が揃っていることを前提にしたものでした。しかしながら、下図右側に示したように、この位相が揃っていない場合も考えられます。今回は、この位相差\(\Delta\)がモーターの左右ユニバーサルジョイントの最終伝達面の角速度にどのような影響を与えるかを解析してみます。
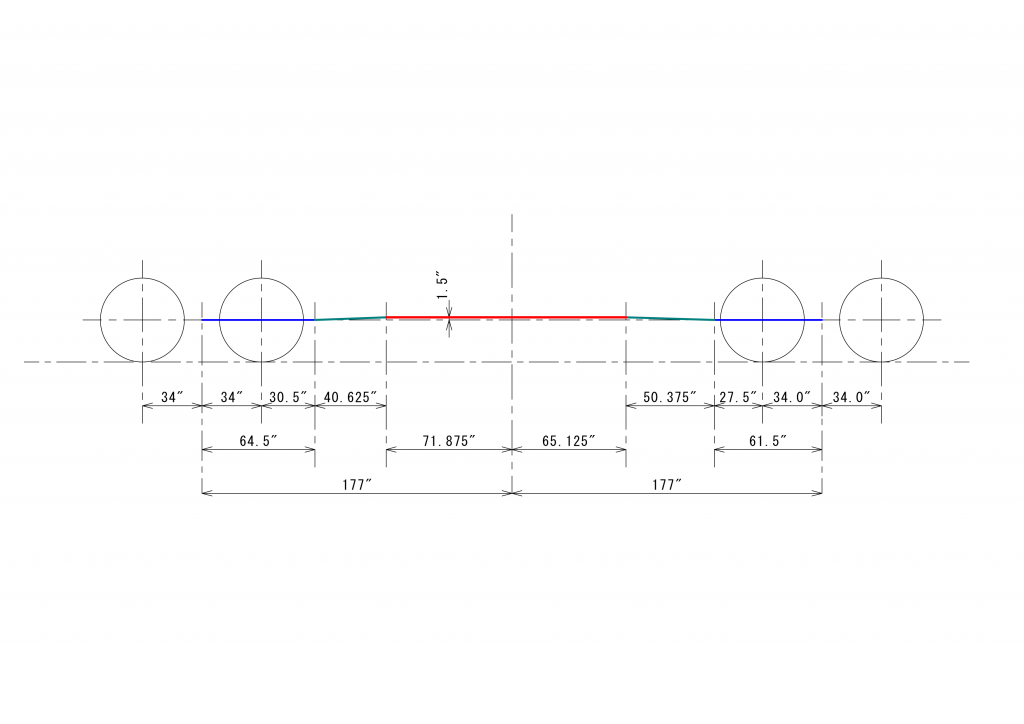
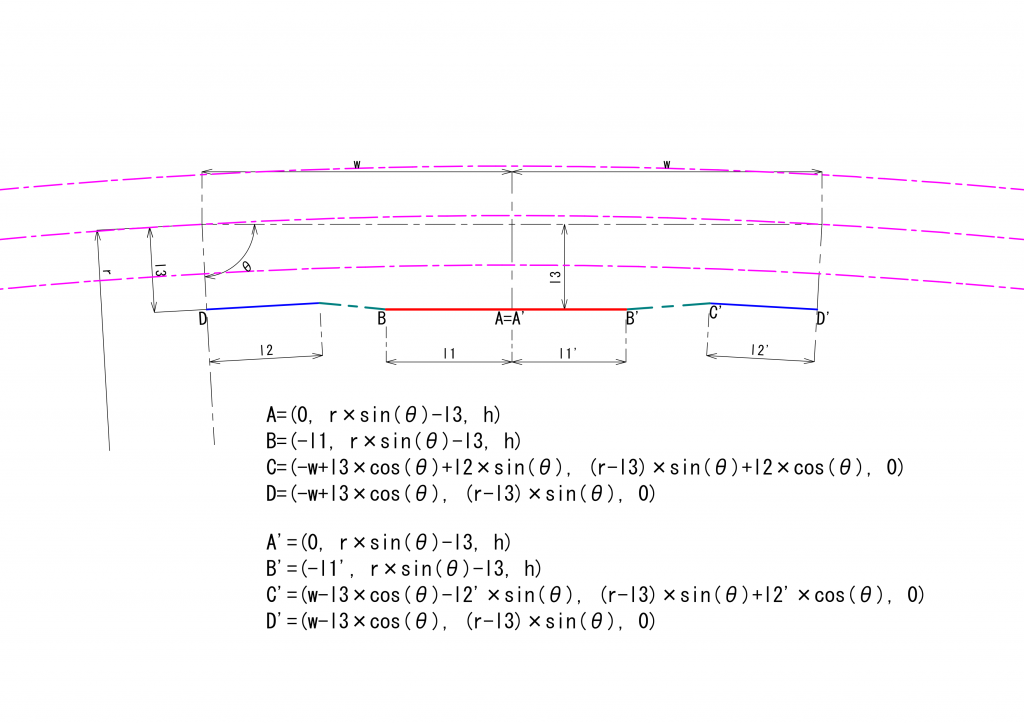
今回の議論では、通常のＭＰギア、つまりジョイントは完全に左右対称の位置にあり、3つの軸が同一平面上にある場合についてのみ議論します。Shayのようにジョイントの位置が左右対称にない場合、ユニバーサルジョイントを構成する3つの軸が同一平面上にない場合、についても同様の議論が成り立ち、同じ傾向と示すと考えられます。
モータに向かって左側のユニバーサルジョイントの駆動面の基準点が角速度\(\omega\)で回転する場合、\(\omega\)に対する最終伝達面の角速度の比は、以前求めたように
\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
で計算できます。
左側のユニバーサルジョイントの回転方向に向かって、右側のユニバーサルジョイントの駆動面の基準点の位相が、\(\Delta\)進んでいるとします。右側のユニバーサルジョイントの角速度は\(-\omega\)となりますので、右側のユニバーサルジョイントの最終駆動面の角速度比は次の式で表すことができます。なお議論を簡単にするために、\(\delta\)は、左右のユニバーサルジョイントで同じ、つまり左右のユニバーサルジョイントの位相はどちらも正しい、あるいはどちらも間違っている、ということを前提とします。
\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(-\omega t-\Delta)+sin^2(-\omega t-\Delta)\cdot {cos}^2(\alpha) – (cos(-\omega t-\Delta)\cdot cos(\delta)-sin(-\omega t-\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
\(cos(-x)=cos(x)\)、\(sin(-x)=-sin(x)\)ですので、上記の式は
\(\frac{cos(\alpha)\cdot cos(\beta) }{cos^2(\omega t+\Delta)+sin^2(\omega t+\Delta)\cdot {cos}^2(\alpha) – (cos(\omega t+\Delta)\cdot cos(\delta)+sin(\omega t+\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
となります。
これらの2つの式から、左側のユニバーサルジョイントの最終伝達面の角速度に対する右側の加速度ユニバーサルジョイントの最終伝達面の角速度の比は
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t+\Delta)+sin^2(\omega t+\Delta)\cdot {cos}^2(\alpha) – (cos(\omega t+\Delta)\cdot cos(\delta)+sin(\omega t+\Delta)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
で表すことができます。
この式は、動力の左右にユニバーサルジョイントで動力を伝動する場合、左右それぞれのユニバーサルジョイントで発生する角速度の変動に加え、左右のユニバーサルジョイントの最終伝達面の角速度の差が発生しうる、ということを言っています。これは、どちらか一方の動力が速く（遅く）回転しようとしているのに、一方の動力はそれを妨げる方向に働くということを意味しており、この比が大きいと、動力伝達の効率を低下させ、スムーズな挙動に影響があると考えられます。
前回までの議論では、\(\Delta=0\)を前提としているのでした。これを上記に代入すると
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)+sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
となります。いつものように、我々の興味のあるのは、\(\delta=0\)、もしくは\(\delta=\frac{\pi}{2}\)の場合です。
\(\delta=0\)の時、\(sin(\delta)=0\)、\(cos(\delta)=1\)ですので、上記の式は、
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta))^2\cdot{sin}^2(\beta)}=1\)
となります。また、\(\delta=\frac{\pi}{2}\)の時、\(sin(\delta)=1\)、\(cos(\delta)=0\)ですので、上記の式は、
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (-sin(\omega t)\cdot cos(\alpha))^2\cdot{sin}^2(\beta)}{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (sin(\omega t)\cdot cos(\alpha))^2\cdot{sin}^2(\beta)}=1\)
となります。従って、\(\Delta=0\)の時、ユニバーサルジョイントの左右の最終伝達面の角速度比は同じであるということが確認できました。この結果は、\(\Delta=0\)の時、左右の挙動は左右対称で同じに解析できるという、これまで暗黙に仮定を置いてきたことを裏付けるものです。
\(\Delta=\frac{\pi}{2}\)とすると、ユニバーサルジョイントの左右の最終伝達面の角速度比は、
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{cos^2(\omega t+\frac{\pi}{2})+sin^2(\omega t+\frac{\pi}{2})\cdot {cos}^2(\alpha) – (cos(\omega t+\frac{\pi}{2})\cdot cos(\delta)+sin(\omega t+\frac{\pi}{2})\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
\(sin(\frac{\pi}{2}\pm\theta)=cos(\theta)\)、\(cos(\frac{\pi}{2}\pm\theta)=\mp sin(\theta)\)、ですので、
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) – (sin(\omega t)\cdot cos(\delta)-cos(\omega t)\cdot cos(\alpha)\cdot sin(\delta))^2\cdot{sin}^2(\beta)}\)
となります。
\(\delta=0\)の時、上記の式は
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – {cos}^2(\omega t)\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) – {sin}^2(\omega t)\cdot{sin}^2(\beta)}\)
となり、\({sin}^2(\theta)+{cos}^2(\theta)=1\)を利用すると
\(\frac{cos^2(\omega t)\cdot{cos}^2(\beta)+sin^2(\omega t)\cdot {cos}^2(\alpha)}{sin^2(\omega t)\cdot{cos}^2(\beta)+cos^2(\omega t)\cdot {cos}^2(\alpha)}\)
と整理できます。
\(\delta=\frac{\pi}{2}\)の時、上記の式は
\(\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha) – {sin}^2(\omega t)\cdot {cos}^2(\alpha)\cdot{sin}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha) -{cos}^2(\omega t)\cdot{cos}^2(\alpha)\cdot{sin}^2(\beta)}\)
\(=\frac{cos^2(\omega t)+sin^2(\omega t)\cdot {cos}^2(\alpha)\cdot{cos}^2(\beta)}{sin^2(\omega t)+cos^2(\omega t)\cdot {cos}^2(\alpha)\cdot{cos}^2(\beta)}\)
となります。
これらの2つの式は、\(\Delta=\frac{\pi}{2}\)の場合、左右の動力で角速度の差が確実に発生するということを言っています。
次回は、どの程度の角速度の差が左右で発生するかをこれらの式に具体的な数字を入れて見てみたいと思います。
この投稿は、加筆修正いたしましたので、こちらをご覧になってください。
長々と続けてきたシリーズ、書き足りないこともあるとは思っていますが、本質的に書くべきことはすべて網羅したと考えていますので、今回でいったん区切りをつけることとします。
ここまで考察してきたことを以下にまとめます。
（１）まずはユニバーサルジョイントの使い方一般について。
（２）模型では、簡易型のユニバーサルジョイントがよく使われます。こちらについても解析を行い、次の結果を得ました。
（３）日本型の電車を中心に、MPギア（もしくはそれに類似する形態の駆動系、以下MPギアで代表）がよく用いられています。こちらの考察を進め、次のような結論や仮説を得ました。
（４）ユニバーサルジョイントを構成する3つの軸が同一平面にない場合の解析も行いました。その結果次の結論を得ました。
最初に述べた、ピンの向きを揃える、を念のため下に図示します。
下は誤った使い方の図です。
このシリーズは、7回目を書いた時点で終わる予定でしたが、次々と考えるべきことが出てきて、私自身の興味もつきず、なんと25回も続けてしまいました。数式ばかりの記事に辟易した人が多かったのではないかと思いますが、これは厳密な議論をすることを目的としたものですので、ご了解ください。さび付いた頭で三角関数やら微分やらベクトルやらと格闘するのは大変でしたが、久しぶりに数学の奥深さを感じたように思います。何度か検証したので誤りはないのではないかと思っていますが、もしもお気づきの点があれば、ご指摘頂ければ幸いです。
ここまで、いろいろな方に示唆をいただき、また貴重な情報をいただきました。個別にお名前を挙げることはしませんが、深く御礼申し上げます。
前々回、前回と、ユニバーサルジョイントの3つの軸が同一平面に存在しない場合を仮定して、角速度がどのように変動するかの具体例をMPギアを例として計算してみました。今回はこれをShayの場合で考察してみます。解析の対象としたのは、前に紹介したGreenbrier, Cheat and Elk Railroadの12号機（おそらくsn3156)です。
1922年版のLocomotive cyclopedia of American practiceに載っている主要寸法を次の図に示します。
この150tのShayは、以前紹介したWestern MarylandのShayに匹敵する最大級のShayです。Western Marylandと同じく、最小半径は22度のであると仮定して議論を進めます。
まずは解析に必要な座標を計算します。駆動軸が平面にあるShayの座標の考え方に、上記の軸の高さを考慮したものが次のようになります。なお、これまでは駆動軸がカーブの内側にある場合と外側にある場合との両方を考えてきましたが、今回は条件の厳しい、カーブの内側にある場合のみを考慮することとします。
エンジンに向かって左側のユニバーサルジョイントの角速度の解析に必要な座標は、\(\theta=cos^{-1}(\frac{w}{r})\)とすると、
\(A=(0, -r\cdot sin(\theta)-{l_3}, h)\)
\(B=(-{l_1}, r\cdot sin(\theta)-{l_3}, h)\)
\(C=(-w+{l_3}\cdot cos(\theta)+{l_2}\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}\cdot cos(\theta),0)\)
\(D=(-w+{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)
となります。
求める角速度比を得るには、\(\vec{AB}\)と\(\vec{BC}\)とのなす角\(\alpha\)、\(\vec{BC}\)と\(\vec{CD}\)とのなす角\(\beta\)、\(\vec{AB}\)と\(\vec{BC}\)との外積\(\vec{AB}\times\vec{BC}\)に対して\(\vec{BC}\)と\(\vec{CD}\)との外積\(\vec{BC}\times\vec{CD}\)がどれだけ回転してるかの角度\(\eta\)を求め、
\(\frac{cos(\alpha)\cdot cos(\beta) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha) – (cos(\omega t)\cdot cos(\delta-\eta)-sin(\omega t)\cdot cos(\alpha)\cdot sin(\delta-\eta))^2\cdot{sin}^2(\beta)}\)
を計算します。
Shayの場合は、エンジンの左側と右側とで寸法が異なることが大半ですので、右側の角速度比は左側と同様の計算方法で別途求める必要があります。まずはエンジンに向かって右側のユニバーサルジョイントの解析に必要な座標は、
\(A’=(0, -r\cdot sin(\theta)-{l_3}, h)\)
\(B’=(-{l_1}’, r\cdot sin(\theta)-{l_3}, h)\)
\(C’=(w-{l_3}\cdot cos(\theta)-{l_2}’\cdot sin(\theta), (r-{l_3})\cdot sin(\theta)+{l_2}’\cdot cos(\theta),0)\)
\(D’=(w-{l_3}\cdot cos(\theta), (r-{l_3})\cdot sin(\theta), 0)\)
となります。
これの座標から、\(\vec{A’B’}\)と\(\vec{B’C’}\)とのなす角\(\alpha’\)、\(\vec{B’C’}\)と\(\vec{C’D’}\)とのなす角\(\beta’\)、\(\vec{A’B’}\)と\(\vec{B’C’}\)との外積\(\vec{A’B’}\times\vec{B’C’}\)に対して\(\vec{B’C’}\)と\(\vec{C’D’}\)との外積\(\vec{B’C’}\times\vec{C’D’}\)がどれだけ回転してるかの角度\(\eta’\)を求めます。
前回触れたように、エンジンの左側の角速度を\(\omega\)とした場合、右側の角速度は\(-\omega\)となりますので、求める角速度比は
\(\frac{cos(\alpha’)\cdot cos(\beta’) }{{cos}^2(\omega t)+{sin}^2(\omega t)\cdot {cos}^2(\alpha’) – (cos(\omega t)\cdot cos(\delta-\eta’)+sin(\omega t)\cdot cos(\alpha’)\cdot sin(\delta-\eta’))^2\cdot{sin}^2(\beta’)}\)
となります。
得られた計算式で、位相が正しい場合と、位相が間違っている場合との角速度の変動を計算した結果を次のグラフに示します。
比較のために、エンジンの中心軸が、台車の軸と水平になった(h=0)場合のグラフと重ねてみたものを示します。
これで見る限り、h=1.5”としても、1%を下回る角速度の変動となりますので、実用上は大きくは影響を与えないであろうということは言えるかと思います。少しでも高さを稼ぎたい理由があったのでしょうか。
いまさら言わなくても、という気がしますが、逆位相の場合に急激に変動が大きくなる傾向は、MPギアの時の計算結果と同じとなります。